En savoir plus sur la composition des fonctions

Cette calculatrice vous permettra calculer une fonction composite $f \circ g$ à partir de deux fonctions $f$ et $g$ que vous fournissez. Notez qu'en général $f \circ g$ n'est pas la même chose que $g \circ f$ donc l'ordre est pertinent.

En calculant la composition $f \circ g$, il y a une fonction interne $g$ et une fonction externe $f$, et vous changez l'ordre, très souvent le résultat varie.

Observez que $f$ et $g$ doivent être des fonctions valablement définies, comme par exemple $f(x) = \sqrt{x}$ et $g(x) = 2x+1$, donc on aurait alors que $(f \circ g)(x) = f(g(x)) = \sqrt{2x+1}$ .

Qu'est-ce qu'une fonction composite ?

Pour former une fonction composite, on évalue une fonction à l'intérieur d'une autre fonction. Soit $f$ et $g$ des fonctions, la fonction composite est définie comme suit

$$\displaystyle (f \circ g)(x) = f(g(x))$$

Quelles sont les étapes pour trouver la fonction composite ?

• Étape 1 : Identifiez les fonctions f et g pour lesquelles vous allez effectuer une composition de fonctions
• Étape 2 : établir clairement la fonction interne et externe. Dans ce cas, nous supposons que f est la fonction externe et que g est la formule interne
• Étape 3 : La fonction composite est définie comme suit : (f◦g)(x) = f(g(x))

Vous pouvez simplifier la sortie résultante de f(g(x)), et en fait, la calculatrice la simplifiera pour vous. Un point important est de réaliser que vous devrez peut-être restreindre le domaine de la fonction composite afin qu'elle soit bien définie.

Qu'est-ce qu'un calculateur de brouillard

Dans ce cas, le brouillard n'est pas le brouillard que vous connaissez, il s'agit de la composition de f et g, écrite sous la forme $f \circ g$.

La composition de fonctions sera aussi algébriquement impliquée que la complexité des fonctions composées. En d'autres termes, la composition de fonctions simples conduira à une fonction composite simple, facile à calculer.

En utilisant ce calculateur composite

L'avantage d'utiliser cette calculatrice composite est que vous obtiendrez la fonction composite calculée et simplifiée dans ses termes les plus simples, mais vous obtiendrez également la fonction composite sous forme de graphique.

Chaîne de fonctions composites

La composition peut être appliquée à plus de deux fonctions. Par exemple, considérons les fonctions $f$, $g$ et $h$. La composition en chaîne est définie comme suit

$$\displaystyle (f \circ g \circ h)(x) = f(g(h(x)))$$

où l'ordre dans lequel vous composez les expressions est pertinent.

Calculatrice du domaine d'une fonction composite

Remarquez que le domaine d'une fonction composée peut être différent de celui des deux fonctions d'origine. Par exemple, voyons à nouveau le cas de $f(x) = \sqrt{x}$ et $g(x) = 2x+1$. Le domaine de f est $[0, \infty)$ et celui de g est $(-\infty, \infty)$, mais comme $(f\circ g)(x) = \sqrt{2x+1}$, le domaine de $f\circ g$ est $[-\frac{1}{2}, \infty)$.

Exemple : composition des fonctions

Calculez et représentez graphiquement : $(f \circ g)(x)$ pour $f(x) = \sqrt{x}$ et $g(x) = 2x-1$.

Solution: On a fourni les fonctions suivantes : $\displaystyle f(x)=\sqrt{x}$ et $\displaystyle g(x)=2x-1$, pour lesquelles nous devons calculer la fonction composite $f \circ g$.

Par définition, la fonction composite $f \circ g$ est définie comme :

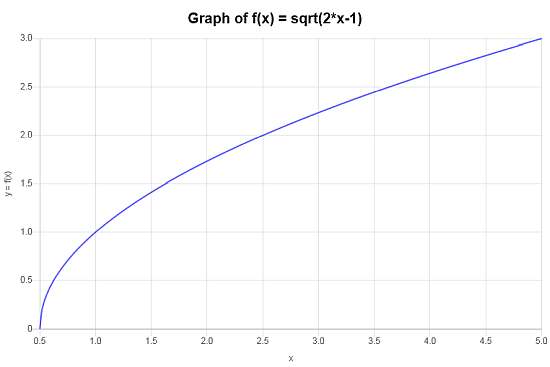
$$\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \sqrt{2x-1} \end{array}$$

Il n'y a rien à simplifier dans ce cas, et alors, la fonction composée que nous recherchons est $f \circ g(x)=\sqrt{2x-1}$.

On obtient le tracé suivant pour la fonction composée $f \circ g(x)=\sqrt{2x-1}$ sur l'intervalle $[-5, 5]$ :

Exemple : calcul de la fonction composite

Calculez et représentez graphiquement : $(f \circ g)(x)$ pour $f(x) = x^{3/2}$ et $g(x) = x+2$. Est-ce que $(f \circ g)(x)$ est identique à $(g \circ f)(x)$ dans ce cas ?

Solution: Ce sont les fonctions que nous devons composer : $\displaystyle f(x)=x^{3/2}$ et $\displaystyle g(x)=x+2$.

Par définition, la fonction composite $f \circ g$ est définie comme :

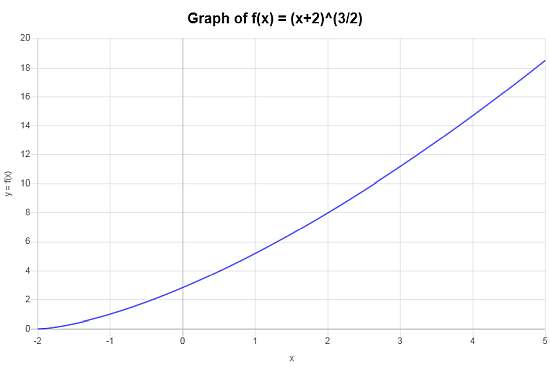
$$\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x+2\right)^{3/2} \end{array}$$

Il n'y a rien à simplifier dans ce cas, et alors, la fonction composée que nous recherchons est $f \circ g(x)=\left(x+2\right)^{3/2}$.

On obtient le graphique suivant pour la fonction composée $f \circ g(x)=\left(x+2\right)^{3/2}$ sur l'intervalle $[-5, 5]$ :

Exemple : exemple de calcul de la fonction composite

Trouvez $(f \circ g)(x)$ pour $f(x) = x^2$ et $g(x) = x-2$ et tracez le graphique de la fonction composée.

Solution: Dans cet exemple, nous devons travailler avec $\displaystyle f(x)=x^2$ et $\displaystyle g(x)=x-2$, ce qui nous oblige à calculer la fonction composite. $f \circ g$.

En utilisant cette définition, la fonction composite $f \circ g$ est définie comme suit :

$$\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x-2\right)^2 \end{array}$$

L'expression ci-dessus doit être simplifiée, et les étapes sont les suivantes :

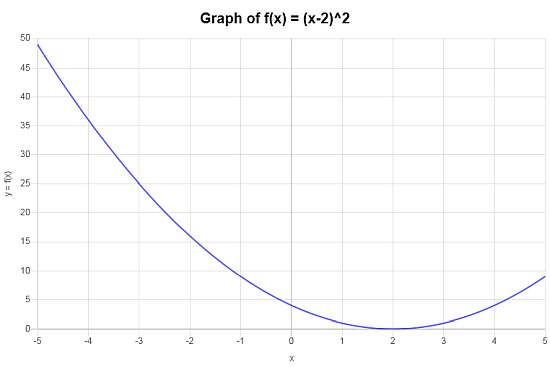
Ainsi donc, après avoir simplifié, la fonction composée que l'on obtient est $f \circ g(x)=x^2-4x+4$.

La fonction composée $f \circ g(x)=x^2-4x+4$ conduit au tracé suivant sur l'intervalle $[-5, 5]$ :

Plus de calculatrices d'algèbre

Fonctions sont l'un des principaux éléments de l'algèbre et du calcul. Et la raison en est qu'elle incarne un moyen d'établir une relation entre deux variables x et y.

De nombreuses applications dépendent des opérations que vous effectuez et également de la le graphique d'une fonction qui contient toutes les informations "stockées" dans la fonction.