En savoir plus sur les équations linéaires

Cette calculatrice vous aidera à représenter graphiquement une équation linéaire que vous lui fournirez. Ainsi, la première étape consiste à fournir une équation linéaire valide, quelque chose comme 2x + 3y = 4, ou vous pouvez également fournir quelque chose qui n'est pas directement simplifié, comme 2/3 x + y = 4/3 x - 1/2 y + 2. Toute expression linéaire valide fonctionnera. .

Une fois que vous avez fourni une équation linéaire valide, la partie facile entre en jeu, car tout ce que vous avez à faire est de cliquer sur "Calculer", et les étapes du processus de représentation graphique de la fonction linéaire vous seront montrées.

Les équations linéaires joueront un rôle important dans de nombreuses opérations, notamment pour résoudre un système d'équations linéaires .

Formule d'équation linéaire

Il existe différentes formes sous lesquelles vous pouvez écrire une formule d'équation linéaire. Les plus courantes sont formes standard qui se présente comme suit

$$a x + by = c$$

Il y a aussi le Forme d'interception de pente qui se présente comme suit

$$y = mx + n$$

Ces deux formes peuvent généralement être converties l'une en l'autre, à quelques exceptions près, notamment la droite verticale exprimée par x = a. Cette droite est verticale et croise l'axe des x en (a, 0). Nous savons que x = a est la forme standard de la droite, mais cette droite n'a pas d'axe de pente (du moins lorsque y est la variable dépendante)

Quelles sont les étapes de la représentation graphique d'une équation linéaire ?

• Étape 1 : Identifiez clairement l'équation disponible
• Étape 2 : voir le coefficient qui multiplie y, s'il est nul, alors vous avez une ligne verticale
• Étape 3 : Si le coefficient qui multiplie y est différent de zéro, vous résolvez alors y afin d'obtenir la valeur de Forme d'interception de pente
• Étape 4 : À l'aide de la forme de l'ordonnée à l'origine de la pente, évaluez la fonction à x = 0 et x = 1, et vous avez alors deux points où la ligne passe par
• Étape 5 : Tracez une ligne en utilisant les deux points que vous avez trouvés comme guide

L'une des façons les plus claires de tracer une ligne est d'avoir deux points par lesquels la ligne passe, car souvent, utiliser la pente pour se guider peut être trompeur.

Solution d'une équation linéaire en une variable

Les élèves sont familiers avec les systèmes d'équations linéaires, et ils comprennent plus ou moins ce qu'il faut faire. Mais ils s'interrogent ensuite sur la solution d'une équation linéaire à une variable. Supposons que vous ayez l'équation linéaire sous la forme de l'ordonnée à l'origine :

$$y = a + bx$$

Alors, comment résoudre ce problème ? Eh bien, elle est déjà résolue : Pour chaque valeur donnée de x, la solution de y est y = a + bx. Donc, à condition que $b \ne 0$, vous avez une infinité de solutions à une équation linéaire.

La situation change lorsque vous avez deux équations linéaires, auquel cas vous devez résoudre les deux équations simultanément .

Les équations linéaires sont-elles si importantes ?

Tu parles ! C'est peut-être l'une des plus importantes de toutes les mathématiques. Et ce, en raison de sa simplicité et pourtant de son vaste champ d'applications.

Exemple : calculatrice d'équations linéaires

Obtenez le graphique de l'équation linéaire suivante : $\frac{1}{3} x + \frac{7}{4} y - \frac{5}{6} = 0$

Solution:

Obtenez l'équation de la ligne sous la forme de l'axe de la pente

L'équation suivante nous a été donnée.. :

$$\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0$$

Simplifier les constantes :

$$\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0$$

Maintenant, en mettant $y$ sur le côté gauche et $x$ et la constante sur le côté droit, on obtient

$$\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}$$

Maintenant, en résolvant pour $y$, en divisant les deux côtés de l'équation par $\frac{7}{4}$, on obtient ce qui suit

$$\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}$$

et en simplifiant on obtient finalement ce qui suit

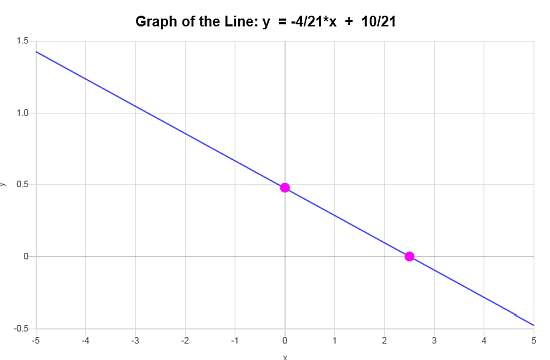
$$\displaystyle y=-\frac{4}{21}x+\frac{10}{21}$$

Conclusion : Nous déduisons que l'équation de la droite sous forme d'ordonnée à l'origine est basée sur les données disponibles est : $\displaystyle y=-\frac{4}{21}x+\frac{10}{21}$, avec une pente de $\displaystyle b = -\frac{4}{21}$ et un ordonnée à l'origine de $\displaystyle n = \frac{10}{21}$.

Compte tenu de ces données, le graphique linéaire fourni montre

Exemple : exemple de calculateur d'équations linéaires

Calculez ce qui suit : $\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}$

Solution: Nous disposons maintenant de l'équation suivante :

$$\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}$$

La première étape consiste à simplifier les constantes :

$$\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}$$

En plaçant $y$ sur le côté gauche et $x$ et le terme constant sur le côté droit, nous obtenons donc

$$\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}$$

Maintenant, nous devons résoudre $y$, et cela est réalisé en divisant les deux côtés de l'équation par $\frac{5}{4}$, et ce qui suit est obtenu

$$\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}$$

et en simplifiant on obtient finalement ce qui suit

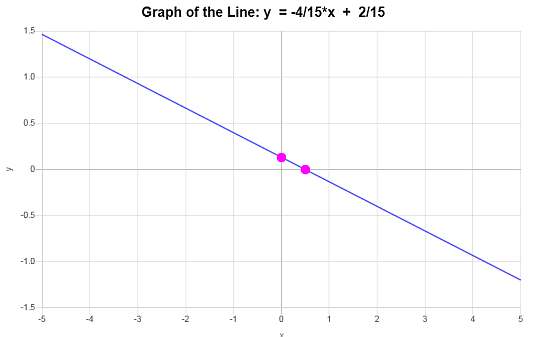
$$\displaystyle y=-\frac{4}{15}x+\frac{2}{15}$$

Conclusion : L'équation de la droite sous la forme pente-interception est, selon les informations fournies, $\displaystyle y=-\frac{4}{15}x+\frac{2}{15}$, avec une pente de $\displaystyle b = -\frac{4}{15}$ et un ordonnée à l'origine de $\displaystyle n = \frac{2}{15}$.

D'après ces données, le graphique linéaire présenté est

Exemple : un autre exemple de calculateur d'équations linéaires

Est-ce que cela représente une ligne : $y = 5$. Si oui, quelles sont ses caractéristiques ?

Solution: Oui, c'est le cas. En effet, lorsque vous avez une expression comme $y = 5$, vous avez une équation linéaire sous forme d'ordonnée à l'origine, avec a = 0 et b = 5. Par conséquent, ce que nous avons est une ligne qui est horizontale, qui croise l'axe des y au point (0, 5).

Plus de calculatrices d'algèbre

Lignes , Équations linéaires et fonctions linéaires jouera toujours un rôle crucial en algèbre, présentant également un lien clair avec certaines propriétés géométriques de base.

En termes d'applications, peut-être Résolution de systèmes d'équations linéaires est l'une des applications les plus courantes des lignes et des équations linéaires.