Cómo utilizar esta calculadora de intercepción de la x con pasos

Esta calculadora te permitirá calcular la intersección x de una recta, y obtendrás todos los pasos mostrados.

La intersección x es el punto en el que la línea cruza el eje x, si es que eso ocurre.

En general, siempre hay una intersección x cuando la pendiente es diferente de cero.

Cuando la pendiente es cero, habrá una intersección x sólo si la línea también cruza el origen. Las líneas verticales también tienen una intersección x.

Cómo encontrar el intercepto de la x con pasos con esta calculadora

Todo lo que tienes que hacer para utilizar esta calculadora es decidir una de las cuatro opciones proporcionadas para definir tu línea. A menudo se proporciona la pendiente y la intersección y, pero también se puede escribir la ecuación de la línea directamente .

Si la ecuación que has proporcionado es válida, la calculadora repasará los pasos necesarios para identificar la intersección x, o para indicar que no se ha podido encontrar ninguna intersección x

¿puedes obtener la intersección x de una recta en forma estándar?

Sí, de hecho, utilizando el forma estándar de la línea es una de las formas más fáciles de calcular la intersección x.

Así, una estrategia común es convertir primero la ecuación de la recta en forma estándar y luego resolver para \(x\) cuando \(y=0\).

¿por qué necesitamos la intersección x?

La intersección x y Intercepción Y de una línea tienen una gran utilidad para dar una intuición geométrica del comportamiento sobre una línea en los ejes de coordenadas \(X - Y\).

Ejemplo de cálculo de la intersección x dada una recta

Conoces la forma estándar de la recta \( \frac{3}{4} x + \frac{4}{5} y = 2\). Encuentra la intersección x de la recta.

Respuesta:

Nos han proporcionado la siguiente ecuación:

\[\displaystyle 2x+y=y+5\]

Entonces, ¿a quién encuentras x interceptar? : Pasando todas las variables y sus coeficientes a la izquierda de la ecuación, y agrupando las constantes a la derecha, obtenemos:

\[\displaystyle 2x+\left(1-1\right)y = 5\]

y simplificando todos los términos que necesitan simplificación, obtenemos que la ecuación en forma estándar es

\[\displaystyle 2x=5\]

El término \( y\) no aparece en el lado izquierdo de la ecuación, por lo que podemos seguir resolviendo para \( x\), lo que nos lleva a

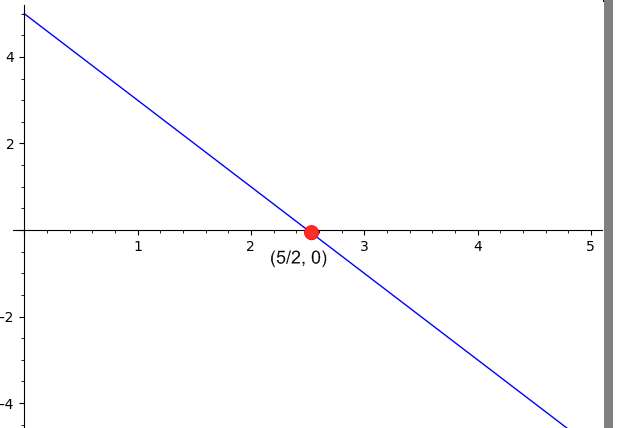
\[ 2 x = 5 \Rightarrow x=\frac{5}{2}\]

Obsérvese que en base a lo anterior, esto corresponde a una línea vertical, que atraviesa el valor \(\displaystyle x=\frac{5}{2}\).

Conclusión : A partir de los datos proporcionados, concluimos que la recta cruza el eje x en \(\displaystyle x = \frac{5}{2}\), por lo que el punto de intersección x correspondiente es \(\displaystyle \left(\frac{5}{2}, 0\right)\).