Berechnung der preiselastizität der nachfrage anhand von stichprobendaten

Verwenden Sie diesen Rechner, um die Preiselastizität der Nachfrage anhand der von Ihnen bereitgestellten Beispieldaten für Preis und nachgefragte Menge zu schätzen.

Sie müssen gültige Beispieldaten angeben, d. h. beide Beispiele (Preis und nachgefragte Menge) müssen positive Werte aufweisen. Sobald Sie Ihre Daten in die Tabelle eingefügt haben, können Sie auf „Berechnen“ klicken, um alle Schritte anzuzeigen.

Beachten Sie, dass dieser Ansatz erfordert, dass die Daten einem bestimmten Muster folgen, das zu einem Log-Log-Modell passt, wobei \(\ln(P)\) und \(\ln(Q)\) als Hilfsvariablen verwendet werden, um ein lineares Regressionsmodell durchzuführen.

Berechnung der preiselastizität anhand von beispieldaten

Um die Preiselastizität zu berechnen, müssen Sie das folgende Hilfsmodell schätzen:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

Beachten Sie, dass dies einem regulären linearen Regressionsmodell entspricht, bei dem die ursprünglichen Variablen Preis und Menge logarithmisch transformiert werden. Deshalb verlangen wir, dass beide Variablen streng positiv sind.

Wie erfolgt die berechnung der elastizität?

• Schritt 1: Identifizieren Sie die Beispieldaten für die angegebenen Variablen für Preis (P) und Menge (Q)
• Schritt 2: Stellen Sie sicher, dass beide Proben die erforderliche Stichprobengröße haben und BEIDE positiv sind, sonst können Sie die Berechnung nicht durchführen
• Schritt 3: Logarithmische Transformation beider Variablen: Berechnen Sie ln(X) und ln(Y)
• Schritt 4: Führen Sie eine zusätzliche lineare Regression für die Variablen ln(X) und ln(Y) durch, wobei ln(X) die unabhängige Variable und ln(Y) die abhängige Variable ist
• Schritt 5: Der für diese Hilfsregression ermittelte Steigungskoeffizient ist die Preiselastizität der Nachfrage nach diesen Daten

Der entscheidende Schritt ist dann die Log-Transformation der Daten, die es uns ermöglicht, die Elastizität basierend auf den Ergebnissen einer linearen Regression zu berechnen, wodurch die Ergebnisse sehr gut interpretierbar werden.

Preiselastizität verstehen

Per Definition wird die Preiselastizität mithilfe der folgenden Formel ermittelt:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

Dies zeigt unter anderem, dass wir die prozentuale Änderung der nachgefragten Menge mithilfe des folgenden Ausdrucks vorhersagen können:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

Dies bedeutet, dass die prozentuale Änderung von Q gleich der prozentualen Änderung von P multipliziert mit der Elastizität ist. Es ist wichtig zu beachten, dass diese Definition gilt punktweise : Das heißt, die Elastizität muss nicht über die gesamte Nachfragekurve hinweg konstant sein. Sie kann es aber, und in diesem Rechner wird eine solche Annahme getroffen.

Interpretation von preiselastizitätskoeffizienten

Wie wir im vorherigen Abschnitt gesehen haben, entspricht die Elastizität \(\varepsilon\) einfach dem Steigungskoeffizienten der logarithmisch transformierten Hilfsregression. Sie hat aber auch eine sehr interessante Interpretation der Randänderung:

• Bei einer zusätzlichen Preisänderung von 1 % ändert sich die nachgefragte Menge um \(\varepsilon \%\)

Dies ist genau das, was die Elastizitätsformel erfordert und impliziert. Beachten Sie, dass dieser Rechner ein Modell schätzt, das davon ausgeht, dass die Daten einem Muster folgen, das eine konstante Elastizität begünstigt, was beispielsweise bei einer linearen Nachfragefunktion nicht der Fall ist.

Faktoren, die die preiselastizität beeinflussen

Die Elastizität spiegelt die Reaktion der Verbraucher auf Preisänderungen wider. Normalerweise ist die Elastizität negativ: Wenn der Preis einer Ware steigt, wird der Käufer wahrscheinlich weniger kaufen, zumindest wenn es sich um eine normale Ware handelt.

Eine Elastizität, deren absoluter Wert größer als 1 (kleiner als -1) ist, wird mit einer elastischen Reaktion auf den Preis bezeichnet, während eine Elastizität, deren absoluter Wert zwischen 0 und 1 (zwischen -1 und 0) ist, mit einer unelastischen Reaktion auf den Preis bezeichnet wird.

Die Wirtschaftstheorie sagt voraus, dass verschiedene Faktoren die Preiselastizität der Nachfrage beeinflussen. Beispielsweise führt das Fehlen oder der Mangel an Ersatzprodukten zu einer größeren Elastizität in absoluten Werten.

Beispielelastizitätsberechnung: verwenden von beispieldaten

Berechnen Sie die Elastizität anhand der folgenden Beispieldaten:

P	Q
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

Lösung : Um aus diesen Daten die Preiselastizität der Nachfrage zu ermitteln, müssen wir ein Log-Log-Regressionsmodell erstellen, bei dem die von uns verwendete unabhängige Variable \(ln(P)\) und die abhängige Variable der natürliche Logarithmus von \(ln(Q)\) ist

Zur Berechnung der Regressionskoeffizienten für diese Hilfsregression muss folgende Tabelle verwendet werden:

	P	Z = ln(P)	Q	W = ln(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

Basierend auf der obigen Tabelle wird Folgendes berechnet:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

Daher werden auf Grundlage der obigen Berechnungen die Regressionskoeffizienten (die Steigung \(m\) und der y-Achsenabschnitt \(n\)) wie folgt ermittelt:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

Daher stellen wir fest, dass die Regressionsgleichung lautet:

\[W = 2.1639 + 0.715 \text{ Z}\]

Da die Hilfsvariablen jedoch \(Z = \ln(X)\) und \(W = \ln(Y)\) sind, schlussfolgern wir, dass die Log-Log-Regressionsgleichung wie folgt lautet:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

Daher ergeben sich auf Grundlage der oben bereitgestellten Informationen das folgende Streudiagramm und Regressionsdiagramm:

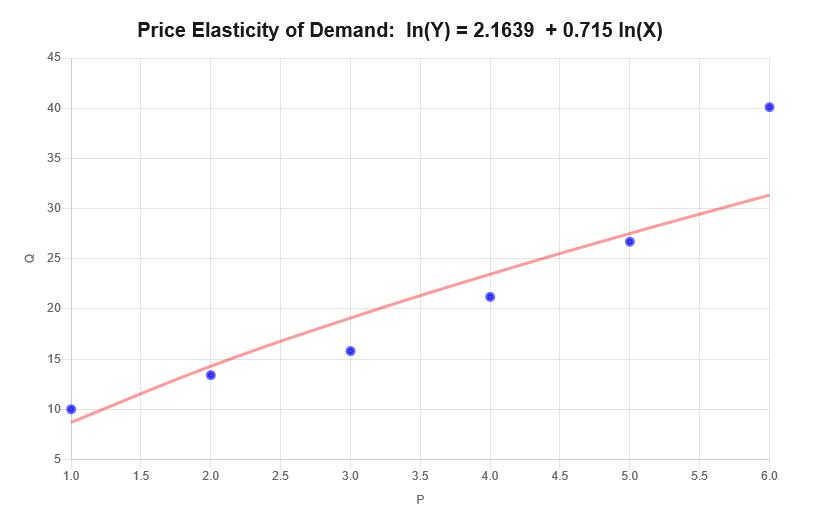
Interpretation

Die Elastizität entspricht in diesem Fall dem Steigungskoeffizienten für die bereitgestellten Daten, d. h. \(\varepsilon = 0.715 \), was wie folgt interpretiert werden kann:

• Bei einer Preiserhöhung von 1 % steigt die nachgefragte Menge im Durchschnitt um 0,715 %.

Weitere interessante rechner

Das Schätzen von Modellen aus Stichprobendaten ist eine entscheidende Fähigkeit, die sowohl in der Statistik als auch in der Wirtschaft benötigt wird. Die Verwendung von Stichprobendaten zur ein Regressionsmodell berechnen ist eine der häufigsten Anwendungen der Verwendung von Beispieldaten zum Modellaufbau.

Aber es kommt oft vor, dass ein reguläres lineares Modell nicht gut genug zu den Daten passt. Wir müssen dann andere funktionale Strukturen ausprobieren. Wir könnten zum Beispiel eine Log-Log-Regression , A logarithmische Regression oder ein Polynomregression , um nur einige zu nennen, die die Variation der abhängigen Variable möglicherweise besser erklären können als die normale Regression.

Die Möglichkeit von Berechnung der Elastizität aus Stichprobendaten wird meist in einem explorativen Umfeld verwendet. Meistens Die Elastizität wird direkt aus der Nachfragefunktion berechnet , sofern verfügbar. Unter anderen Umständen wird die Elastizität anhand eines Paares von Preis-Nachfrage-Punkten geschätzt, wobei Bogenelastizitätsformel .