Frage 1: Die Formeln für die kleinste quadratische Linie wurden durch Lösen des Gleichungssystems gefunden

\[nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

Lösen Sie diese Gleichungen für b und m, um stirbt zu zeigen

\[\begin{align} & m=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left(\sum{{{x}^{2}}} \right)-{{\left( \sum{x} \right)}^{2}}} \\ & b=\frac{\sum{y-m\left( \sum{x}\right)}}{n} \\ \end{align}\]

Lösung: Von

\[ nb+m\left( \sum{x} \right)=\sum{y}\]

\[b\left( \sum{x} \right)+m\left( \sum{x^2} \right)=\sum{xy}\]

Wir haben zwei Gleichungen und zwei Unbekannte (m und b)

Wir erhalten das Multiplizieren der ersten ersten mit \(\left( \sum{x} \right)\) und der zweiten mit -n

\[\begin{align} & nb\left( \sum{x} \right)+m{{\left( \sum{x} \right)}^{2}}=\left( \sum{y}\right)\left(\sum{x} \right) \\ & -nb\left( \sum{x} \right)-mn\left( {{\sum{x}}^{2}}\right)=n\sum{xy} \\ \end{align}\]

und jetzt diese gehören:

\[m\left( {{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right) \right)=\left( \sum{x} \right)\left(\sum{y} \right)-n\left( \sum{xy} \right)\]

\[\Rightarrow \,\,\,\,m=\frac{\left( \sum{x} \right)\left( \sum{y} \right)-n\left( \sum{xy} \right)}{{{\left( \sum{x} \right)}^{2}}-n\left( {{\sum{x}}^{2}} \right)}=\frac{n\left( \sum{xy} \right)-\left( \sum{x} \right)\left( \sum{y} \right)}{n\left( {{\sum{x}}^{2}} \right)-{{\left( \sum{x} \right)}^{2}}}\]

Nun aus diesem Teil:

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\]

wir können für b :: ::

\[nb+m\left( \sum{x} \right)=\left( \sum{y} \right)\,\,\Rightarrow \,\,\,nb=\left( \sum{y} \right)-m\left( \sum{x} \right)\,\Rightarrow \,\,\,b=\frac{\left( \sum{y} \right)-m\left( \sum{x} \right)}{n}\]

Frage 2: Bestimmen Sie den Korrelationsko-

Waldbrände und Hektar brennen. Die Anzahl der Brände und die Anzahl der verbrannten Morgen sind wie folgt

Feuer (x)	72	69	58	47	84	62	57	45
Morgen (y)	62	41	19	26	51	Teile	30	Teile

Lösung: (a) Das folgende Streudiagramm wird erhalten:

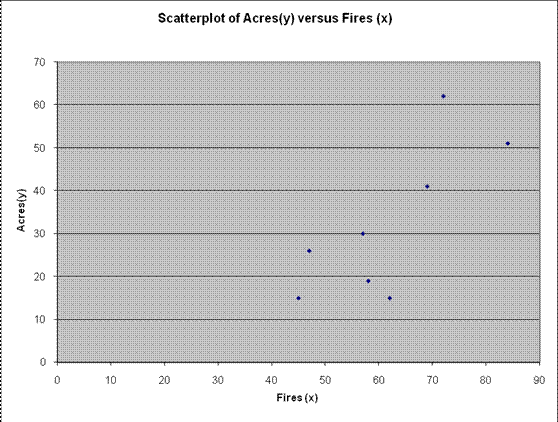
Basierend auf dem obigen Streudiagramm beobachten wir, dass es einen moderaten bis starken Grad an positiver linearer Assoziation gibt.

(b) Andererseits haben wir die folgende Tabelle, die die Berechnungen zeigt, die zur Berechnung der Pearson-Korrelation erforderlich sind: Wir erhalten

Die Pearson-Korrelation r wird berechnet als

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {17216}-{494}\times {259}}{\sqrt{8\times {31692}-{494}^{2}}\sqrt{8\times 10513-{259}^{2}}}\]

\[=0.7692\]

(c) Der Bestimmungskoeffizient beträgt

\[{{r}^{2}}={0.7692}^{2}= {0.5917}\]

was bedeutet, dass 59,17% der Variation in Acres (y) durch Fires (x) erklärt werden.

(d) Die Regressionskoeffizienten werden berechnet

\[b=\frac{n\left( \sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}} \right)-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}=\frac{8 \times {17216}-{494}\times {259}}{8 \times {31692}-{494}^{2}}= 1.0297\]

and

\[a=\bar{y}-b \bar{x}={32.375}{+} {1.0297}\,\cdot \, {61.75} = {-31.208}\]

Dies bedeutet, dass die Regressionsgleichung lautet

\[\hat{y}= {-31.208}{+}{1.0297}\,x\]

Graphically:

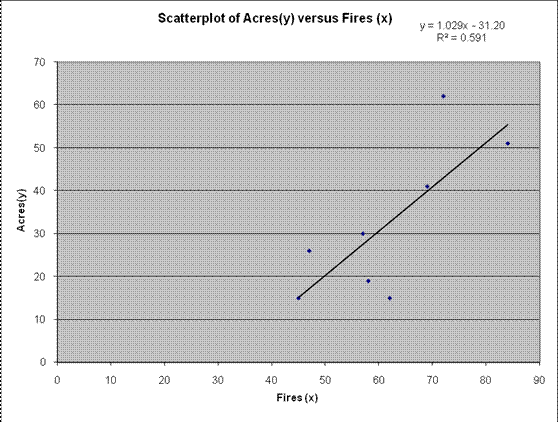
Frage 3: Sie haben eine Studie durchgeführt, um festzustellen, ob die durchschnittliche wöchentliche Zeit im Computerraum und die Kursnote in einem Computerkurs miteinander korrelierten. Welche Schlussfolgerung würden Sie aus den unten angegebenen Daten zu diesem Thema ziehen?

student	# hours in lab	Course Grade
1	20	96
2	11	51
3	16	62
4	13	58
5	89
6	15	81
7	10	46
8	10	51

Lösung: Die folgende Tabelle zeigt die Berechnungen, die zur Berechnung von Pearson erforderlich sind Unterscheidet r : Wir bekommen

Die Pearson-Rechte wird als

\[r = \frac{n\sum\limits_{i=1}^{n}{{{x}_{i}}{{y}_{i}}}-\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}{\sqrt{n\left( \sum\limits_{i=1}^{n}{x_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{x}_{i}}} \right)}^{2}}}\sqrt{n\left( \sum\limits_{i=1}^{n}{y_{i}^{2}} \right)-{{\left( \sum\limits_{i=1}^{n}{{{y}_{i}}} \right)}^{2}}}} = \frac{8 \times {7925}-{112}\times {534}}{\sqrt{8\times {1660}-{112}^{2}}\sqrt{8\times 38224-{534}^{2}}}\]

\[=0.9217\]

Wir wollen die Signifikanz des Korrelationsko. Genauer sagte wollen wir testen

\[\begin{align}{{H}_{0}}:\rho {=} 0 \\ {{H}_{A}}:\rho {\ne} 0 \\ \end{align}\]

Um die Nullhypothese zu testen, verwenden wir einen t-Test. Die t-Statistik wird als

\[t= r \sqrt{\frac{n-2}{1-{{r}^{2}}}}= {0.9217} \times \sqrt{\frac{6}{1-{0.9217}^2}}= {5.8198}\]

Der zweiseitige p-Wert für diesen Test wird als

\[p=\Pr \left( |{{t}_{6}}|>5.8198 \right)=0.0011\]

Seit \(p = 0.0011 {<} 0.05\) und dies bedeutet, dass wir die Nullhypothese H ablehnen ₀ .

Daher haben wir die Befugnisse, um die Rechte zu untermauern, dass die Rechte zwischen der Anzahl der Stunden im Labor und der Kursnote, die von Null abweicht.