Über diesen bogenelastizitätsrechner

Verwenden Sie diesen Rechner, um die Preiselastizität zu schätzen, wenn Sie Informationen über Preis und Nachfrage an zwei Punkten haben. Dies gilt für ein gegebenes \(P_1\), Sie haben eine bestimmte nachgefragte Menge \(Q_1\), und wenn sich der Preis dann auf \(P_2\) ändert, reagiert die nachgefragte Menge mit einer Änderung auf \(Q_2\).

Sie müssen gültige numerische Werte für Preise und die damit verbundenen nachgefragten Mengen angeben. Sobald Sie diese Informationen in die entsprechenden Felder eingegeben haben, klicken Sie auf die Schaltfläche „Berechnen“, um alle Schritte des Berechnungsprozesses anzuzeigen.

In der Wirtschaftstheorie wird davon ausgegangen, dass bei normalen Gütern die nachgefragte Menge als Reaktion auf eine Preiserhöhung zurückgeht.

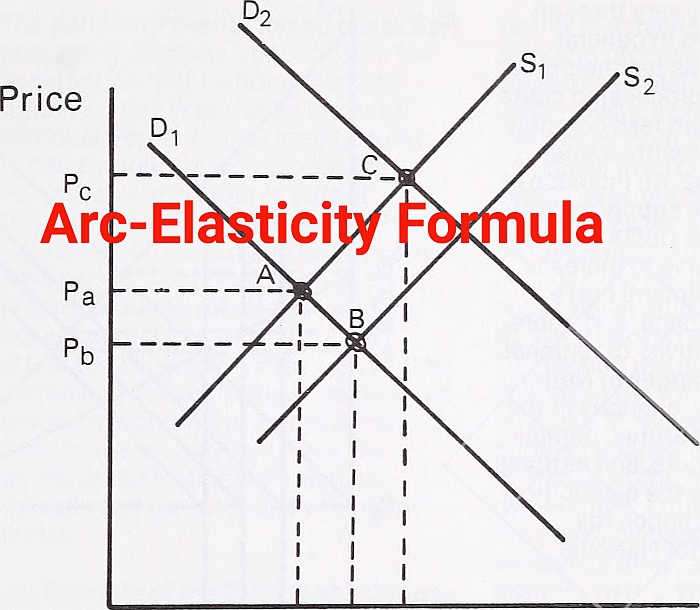
Was sie über die arc-elastizität der nachfrage wissen müssen

In der Wirtschaft ist die Elastizität ein numerisches Maß für die Reaktion der Nachfrage auf Preisänderungen. Wenn der Preis um einen bestimmten Betrag steigt, wird eine Reaktion bei der nachgefragten Menge beobachtet, und die relative prozentuale Änderung der nachgefragten Menge im Vergleich zur relativen prozentualen Änderung des Preises nennen wir die Preiselastizität der Nachfrage.

Mathematisch ausgedrückt würde dies durch diese Formel ausgedrückt:

\[ \text{Elasticity} = \displaystyle \frac{\%\Delta Q}{\%\Delta P}\]

Wir müssen wissen, dass die Elastizität punktweise ist. Wenn wir also eine kleine, aber endliche Preisänderung vornehmen, die als \(\Delta P\) bezeichnet wird, nähern wir uns nur dem Wert der wahren punktweisen Elastizität an

Infinitesimale preisänderungen nutzen

Eine bessere Abstraktion hierfür wäre die Verwendung eines infinitesimal klein Preisänderung. In diesem Fall würden wir einen GENAUEN Ausdruck für die Elastizität erhalten, indem wir verwenden Derivate , was geschrieben werden würde als

\[ \text{Elasticity} = \displaystyle \frac{dQ}{dP}\frac{P}{Q}\]

Im Kontext der obigen Formel ist \(\frac{dQ}{Q}\) die infinitesimale prozentuale Änderung der nachgefragten Menge im Vergleich zur infinitesimalen prozentualen Änderung des Preises, die \(\frac{dP}{P}\) beträgt

Bogenelastizitätsformel

Oft haben wir keinen Zugriff auf die tatsächliche Nachfragefunktion, die für Differenzierungszwecke erforderlich wäre, und wir verfügen nur über diskrete Daten. Eine Methode zur besseren Annäherung an die Elastizität ist die Verwendung dieser Formel:

\[ \varepsilon_{ARC} = \displaystyle \frac{Q_2 - Q_1}{P_2 - P_1}\frac{P_1 + P_2}{Q_1 + Q_2}\]

Das ist eine Vereinfachung von

\[ \varepsilon_{ARC} = \displaystyle \frac{Q_2 - Q1}{P_2 - P_1}\frac{(P_1 + P_2)/}{(Q_1 + Q_2)/2}\]

Dies bedeutet, dass wir einen Durchschnitt der entsprechenden Punkte verwenden, um die prozentualen Änderungen bei Preis und nachgefragter Menge zu schätzen.

Schritte zur verwendung der arc-elastizitätsformel

• Schritt 1: Identifizieren Sie die Preispunkte P1 und P2 und identifizieren Sie die entsprechenden nachgefragten Mengen als Q1 und Q2, indem Sie die richtige Zuordnung herstellen, welcher Preis welcher nachgefragten Menge entspricht
• Schritt 2: Sobald Sie P1, P2, Q1 und Q2 haben, verwenden Sie die Formel e = (Q2 - Q1)/(P2 - P1)*(P1 + P2)/(Q1 + Q2)
• Schritt 3: Dann interpretieren Sie die Elastizität e als die prozentuale Änderung der nachgefragten Menge als Folge einer 1%igen Preisänderung

Beachten Sie, dass die Elastizität häufig negativ ist, da eine Preiserhöhung meistens zu einer Verringerung der nachgefragten Menge führt. Es ist in Ordnung, die Elastizität als negative Zahl anzugeben, aber beachten Sie, dass sie manchmal als absoluter Wert angegeben wird.

Praktische anwendungen der bogenelastizität der nachfrage

Die Elastizität der Nachfrage spielt in der Mikroökonomie eine Schlüsselrolle, da sie ein Bild der Kundenstimmung in Bezug auf ihre Sensibilität gegenüber Preisänderungen vermittelt. Wenn Unternehmen in einem Bereich mit niedrigen Elastizitätswerten (zwischen -1 und 0) tätig sind, der als unelastischer Bereich bezeichnet wird, besteht Spielraum für Preiserhöhungen und dennoch eine relativ moderate Verringerung der nachgefragten Menge, was zu einer Nettoumsatzsteigerung führt.

Wenn Unternehmen hingegen in einem Bereich mit hohen Elastizitätswerten (weniger als -1) tätig sind, dem sogenannten Elastizitätsbereich, führen Preiserhöhungen zu relativ großen Verringerungen der nachgefragten Menge, was zu einem Nettorückgang des Umsatzes führt.

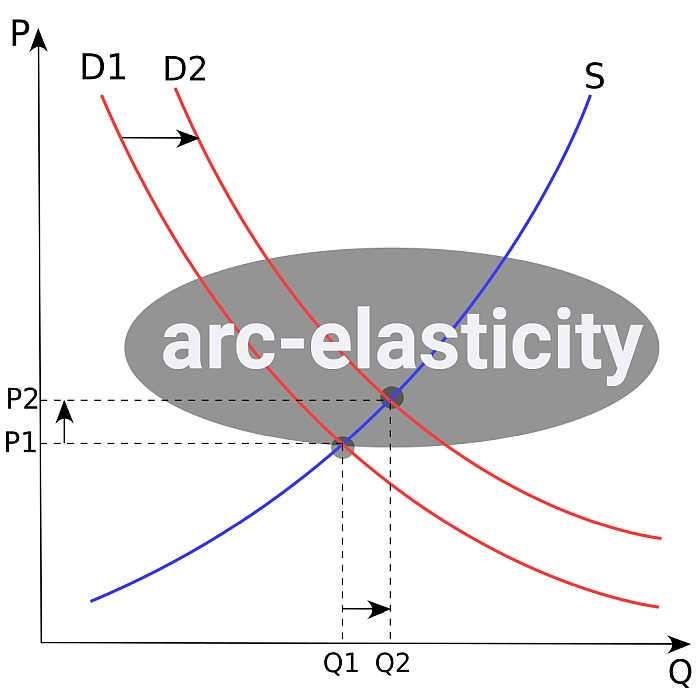
Beispiel zur schätzung der bogenelastizitätsformel

Ein bestimmtes Gut gilt als normales Gut und seine nachgefragte Menge sinkt, wenn der Preis steigt. Bei einem anfänglichen Preis von 25 USD betrug die nachgefragte Menge 200 Einheiten, und als der Preis auf 28 USD erhöht wurde, sank die nachgefragte Menge auf 170. Schätzen Sie anhand dieser Informationen die Preiselastizität der Nachfrage.

Lösung: Wir müssen die Bogenelastizität auf der Grundlage der folgenden Informationen für zwei Preispunkte und die entsprechenden nachgefragten Mengen berechnen

Price 1 \((P_1)\) =	$\(25\)
Price 2 \((P_2)\) =	$\(28\)
Quantity Demanded 1 \((Q_1)\) =	\(200\)
Quantity Demanded 2 \((Q_2)\) =	\(170\)

In diesem Fall muss die Bogenelastizitätsformel verwendet werden. Die Formel lautet:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

Um die Berechnung durchzuführen, müssen wir nur die entsprechenden Werte einsetzen:

\[ \begin{array}{ccl} \varepsilon_{ARC} & = & \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1} \right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right) \\\\ \\\\ & = & \displaystyle \displaystyle \left( \frac{170 - 200}{28 - 25} \right) \left( \frac{25 + 28}{200 + 170} \right) \\\\ \\\\ & = & -1.432 \end{array}\]

Die Bogenelastizität beträgt in diesem Fall \(\varepsilon = -1.432 \), was wie folgt interpretiert werden kann:

• Bei einer Preiserhöhung von 1 % sinkt die nachgefragte Menge im Preisbereich zwischen 25 und 28 US-Dollar im Durchschnitt um 1,432 %.

Andere elastizitätsrechner

Die Berechnung der Preiselastizität der Nachfrage kann verschiedene Formen annehmen. Eine Form ist das, was wir in diesem Rechner tun, indem wir die Bogenelastizitätsformel verwenden, bei der zwei Punkte des Preises und der nachgefragten Menge verfügbar sind

Wir können dies weiterführen mit diesem Bogenelastizitätstabellenrechner , in der Sie eine Tabelle mit Preis und nachgefragter Menge bereitstellen und die Elastizität Punkt für Punkt durch Näherung mit der Bogenelastizität berechnet wird.

In einigen speziellen Fällen werden Sie eine konstante Elastizität annehmen wollen und diese Elastizität aus dem Beispieldatenrechner verwenden, der nur dann brauchbare Ergebnisse liefert, wenn die Preis- und Nachfragedaten einem geeigneten Log-Log-Muster .

Die Idee ist, dass wir eine tatsächliche Nachfragefunktion haben, in der wir einfach Berechnen Sie die Elastizität aus der Nachfragefunktion , wodurch eine genaue punktweise Schätzung der Elastizität erreicht wird, anders als im Fall der Bogenelastizität, bei der es sich um einen Näherungswert handelt.