Arc-Elasticity Formula for a Table

The arc-elasticity of demand formula allows you to estimate the elasticity at the points given at a demand schedule table, without having an explicit formula for the demand function.

What you need to provide is a table with a column for price and a column for quantity demanded. Once that is typed or pasted in the spreadsheet provided, you will click on "Calculate" to get the corresponding arc-elasticities computed for you.

Observe that this only an approximation: the ideal situation is to compute elasticities using the demand function, by using derivatives.

Steps for using Arc-Elasticity for a Table

The arc elasticity formula is:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

and this can be applied to consecutive points in a demand schedule table. You will follow the these steps:

• Step 1: Correctly tabulate your values for price (P) and quantity demanded (Q)
• Step 2: You could create columns for Q2 - Q1, P2 - P1, Q1 + Q2 and P1 + P2 if you want to make the calculations more clear, or you can compute the formula directly
• Step 3: There will be one skipped point in the table, since the arc-elasticity takes a point on the table and the point that immediately follows in the table

Using this arc-elasticity approximation will provide you with an excellent picture of the sensitivity to price changes for the specific good being analyzed, even though it is only approximation.

The more demand points we have, the better the approximation will be, especially if those price points are close together.

What does the arc elasticity measure?

The arc-elasticity aims at providing an approximation of the true elasticity at a given point. The actual elasticity from the demand curve is computed by :

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

One could argue that arc-elasticity is only an approximation, so then how come it has any value. The answer to that is that for elasticity analysis, and for sensitivity analysis in Economics in general, we are interested more about ranges than very specific points.

Indeed, for microeconomics purposes, it is useful to know whether we are in an inelastic range or not, rather than the very specific value of the elasticity

It is not that the specific value is not important, as it is indeed a good to have it, but arc-elasticities are often a good approximation, and they will give us very precise representations of what type of elasticity range we are facing.

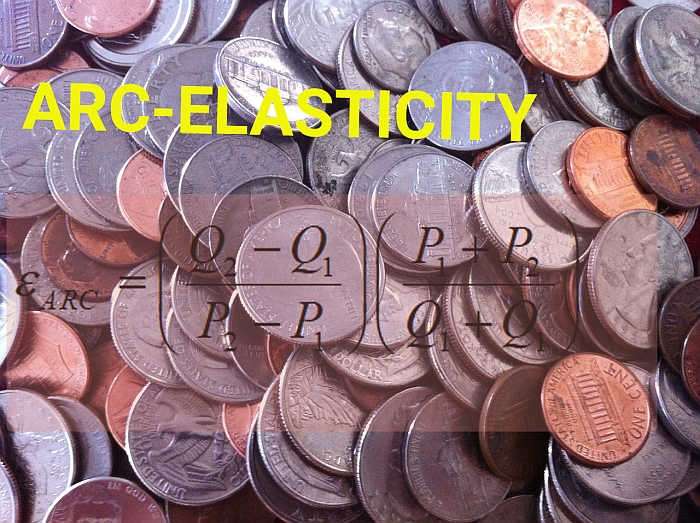
Example

Consider the following demand table with information about price and quantity demandeded

Provide the arc-elasticity approximation for the data points in this table.

P	Q
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

Solution: In order to approximate the price elasticity of demand from these data, we need to use the following arc-elasticity formula

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

By applying the formula above to all pairs of consecutive data points, we find the following arc-elasticities:

P	Q	Arc Elasticity
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

Interpretation

The table found shows the approximate price elasticity of demand for each of the price points provided. These values can be approximately use to determine elastic and inelastic ranges for the provided demand schedule.

Other Economic Calculators

If you are working in Econometrics, this regression calculator will likely be useful, especially because it shows all the steps of the process of calculation of regression coefficients.

You can also use a log-log equation to estimate a demand curve with constant elasticity.