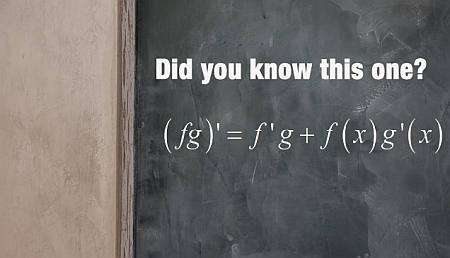Solventes Cálculo

Regra do produto

Instruções: Use esta calculadora para usar a Regra do Produto, para derivar uma determinada função, mostrando todas as etapas. Por favor, digite a função que deseja encontrar a derivada na caixa de formulário abaixo.

Mais sobre a regra do produto

Esta calculadora o ajudará a encontrar a derivada de funções usando a Regra do Produto. Para usar a calculadora, você precisa fornecer uma função válida para a qual haja um produto envolvido. Um exemplo de uma função válida poderia ser algo como f(x) = x*sin(x) ou algo como g(x) = sin(x)*cos(x), apenas para mencionar alguns. Em seguida, estamos digitando a função para a qual você deseja usar a regra do produto, você deve clicar em, basta clicar no botão "Calcular" e todas as etapas dos cálculos serão fornecidas para você. Uma das primeiras regras da derivada que você aprenderá é de fato a Regra do Produto, já que a maioria das funções que você constrói a partir de funções elementares usa o produto de funções.

Fórmula da regra do produto

Aprendendo sobre regra derivada é talvez o primeiro que você fará ao aprender como encontre a derivada de uma função. E uma das primeiras regras que você vai aprender é a regra do produto, sem dúvida. A regra do produto, simplificando, é uma regra que ajuda a calcular a derivada de um produto de funções. A fórmula da regra do produto é:

\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x)

Etapas para usar a regra do produto

Passo 1: Identifique claramente as funções f(x) e g(x) que formam o produto com o qual você está trabalhando
Passo 2: Faça simplificações, se necessário, mantendo a estrutura do produto
Passo 3: Use a fórmula da regra do produto: $(f(x) g(x))' = f'(x) g(x) + f(x) g'(x)$ que envolve substituir o valor das funções f(x) e g(x), bem como de suas derivadas f'(x) e g'(x)

Ao trabalhar com uma derivada de regra de produto, você basicamente obtém a derivada do produto com base no conhecimento das funções individuais e suas derivadas.

Que outras regras derivadas existem?

Além da regra do produto, existem outras regras importantes como a regra da linearidade, a Regra Do Quociente que afirma que $\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}$ , e o Regra Da Cadeia , que afirma que $\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)$ .

Você também encontrará outras regras mencionadas por aí, como a regra da potência, que indica que $\frac{d}{dx} x^n = n x^{n-1}$ , para uma constante $n$ .

Dicas e truques

A regra do produto pode ser considerada uma regra de multiplicação derivada, e a regra do produto desempenha um papel crucial no Cálculo, por isso vale a pena aprendê-la bem.

Observe que no caso de funções multivariáveis, pode-se utilizar a regra da multiplicação de matrizes, para operar a regra do produto.

Exemplo: usando a regra do produto

Calcule a derivada de: $f(x) = (x-1)(2x+1)$

Solução: Consideramos a seguinte função $\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)$ , que precisa ser diferenciada.

\displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)

By using the Product Rule:

\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)

By linearity, we know

\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)

and

\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)

, so plugging that in:

\displaystyle = \,\,

\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)

Since the derivative of a constant is 0, we find that:

\displaystyle = \,\,

\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)

It is known that

\frac{d}{dx}\left(x\right) = 1

\displaystyle = \,\,

\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)

So, we directly get:

\frac{d}{dx}\left( 2x \right) = 2

\displaystyle = \,\,

\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)

and then we find

\displaystyle = \,\,

\displaystyle 2x+1+2\left(x-1\right)

Note that

(2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2

, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\displaystyle = \,\,

\displaystyle 2x+1+2x-2

Grouping the terms with

x

\displaystyle = \,\,

\displaystyle \left(2+2\right)x+1-2

Grouping together numerical values and operating the terms that were grouped with

x

\displaystyle = \,\,

\displaystyle 4x+1-2

Reducing the integers that can be subtracted together:

\displaystyle 1-2 = -1

\displaystyle = \,\,

\displaystyle 4x-1

Conclusão : Portanto, conclui-se que a derivada da função é:

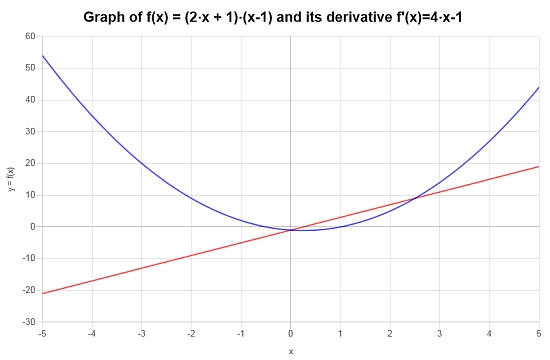
f'(x) = 4x-1

Graficamente, o gráfico a seguir retrata a situação:

Exemplos de regras de produto

Encontre a derivada de: $f(x) = x \sin(x)$

Solução: Neste exemplo, a função dada é $\displaystyle f(x)=x\sin\left(x\right)$ . Vamos encontrar sua derivada

\displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)

Usamos a Regra do Produto:

\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)

Diferenciando diretamente encontramos:

\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)

Então, depois de simplificar, obtemos que:

\displaystyle = \,\,

\displaystyle x\cos\left(x\right)+\sin\left(x\right)

Conclusão : Portanto, descobrimos que a derivada é dada pela seguinte fórmula:

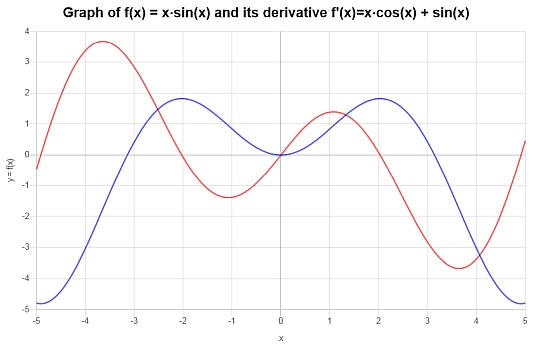
f'(x) = x\cos\left(x\right)+\sin\left(x\right)

O seguinte gráfico é construído para a função e sua derivada:

Exemplo: cálculo de outra regra de produto

Diferencie a seguinte função $f(x) = x (x+1)^2$ .

Solução: Finalmente, para este exemplo, a função dada é $\displaystyle f(x)=x\left(x+1\right)^2$ . Como existe um produto de função, podemos usar a regra do produto para diferenciação.

\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)

Usamos a Regra do Produto:

\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)

Sabemos que

\frac{d}{dx}\left(x\right) = 1

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2

Usando a regra da potência para um expoente constante:

\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)

\displaystyle = \,\,

\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2

Por linearidade, conhecemos

\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)

, então inserindo isso:

\displaystyle = \,\,

\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2

A derivada de uma constante é 0, então:

\displaystyle = \,\,

\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2

Sabemos que

\frac{d}{dx}\left(x\right) = 1

\displaystyle = \,\,

\displaystyle \left(2x+1\right) x+\left(x+1\right)^2

que então leva a

\displaystyle = \,\,

\displaystyle \left(x+1\right)^2+2\left(x+1\right)x

Expandindo os termos:

\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)

\displaystyle = \,\,

\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x

Observe que

(x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1

, pois podemos usar a propriedade distributiva em cada termo da expressão da esquerda, em relação aos termos da direita

\displaystyle = \,\,

\displaystyle x^2+2x+1+2\left(x+1\right)x

Observe que

(x+1) \cdot (x) = x^2+1x = x^2+x

, devido ao fato de podermos usar a propriedade distributiva em cada termo da expressão da esquerda, em relação aos termos da direita

\displaystyle = \,\,

\displaystyle x^2+2x+1+2\left(x^2+x\right)

Obtemos

(2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x

, usando a propriedade distributiva em cada termo da expressão à esquerda, em relação aos termos à direita

\displaystyle = \,\,

\displaystyle x^2+2x+1+2x^2+2x

Agrupando os termos com

x

x^2

\displaystyle = \,\,

\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1

Juntando os inteiros e simplificando os termos que foram agrupados com

x

x^2

\displaystyle = \,\,

\displaystyle 4x+3x^2+1

Então nós conseguimos

\displaystyle = \,\,

\displaystyle \left(3x+1\right)\left(x+1\right)

Conclusão : Com base no que foi calculado acima, verifica-se que a derivada correspondente é:

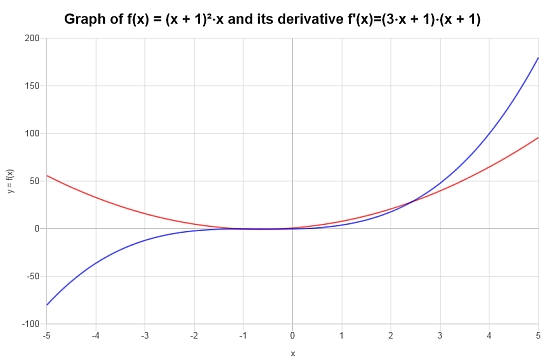
f'(x) = \left(3x+1\right)\left(x+1\right)

O seguinte gráfico é obtido para a função dada no intervalo $[-5, 5]$ :

Mais calculadoras derivadas

Poucas pessoas discordarão dessa diferenciação junto com a integração e o ponto central do Cálculo. Calculando uma derivada é uma habilidade crucial que você precisará aprender como um estudante de cálculo.

Você pode aprender diferentes 'sabores' de diferenciação, incluindo diferenciação parcial assim como diferenciação implícita , que são usados em diferentes contextos de aplicativos.

As aplicações incluem Linha tangente cálculo, que é o mesmo que um Aproximação Linear , bem como o uso de derivadas de ordem superior, começando com derivadas de segunda ordem .