Calculadora de período e frequência

Ao lidar com funções periódicas, existem alguns parâmetros cruciais que precisam ser calculados, e estes são o período (\(P\)) e a frequência (\(f\)).

O período \(P\) de uma função periódica corresponde ao número que satisfaz a seguinte propriedade:

\[f(x+P) = f(x)\]

para todos os valores de \(x\). Observe que nem todas as funções possuem um ponto. Aqueles que o fazem são chamados funções periódicas .

Período de algumas funções comuns

Funções trigonométricas são exemplos de funções periódicas. Por exemplo, se considerarmos a função \(f(x) = \sin x\), seu período é \(2\pi\), conforme o gráfico abaixo:

Para \(\cos x\) também temos o período \(2\pi\). Confira o gráfico abaixo:

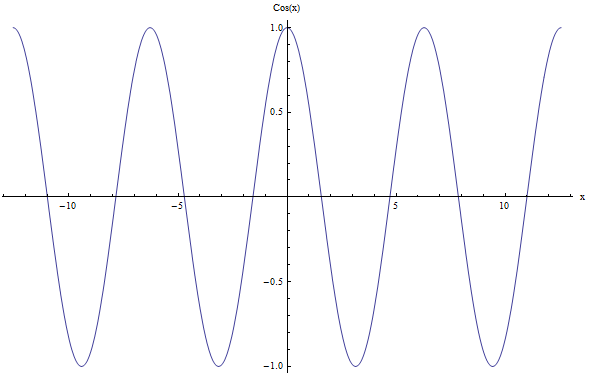
Período de outras funções trigonométricas

Lembre-se que a função cossecante \(\csc x\) é o inverso de \(\sin x\), isto é \(\csc x = \frac{1}{\sin x}\), então o período de \(\csc x\) também é \(2\pi\).

Da mesma forma, a função secante \(\sec x\) é o inverso de \(\cos x\), isto é \(\sec x = \frac{1}{\cos x}\), então o período de \(\sec x\) é \(2\pi\) também.

E a tangente? A função tangente \(\tan x\) é um pouco diferente porque seu período é \(\pi\). De fato, seu gráfico parece diferente do seno e do cosseno, mas a tangente também é periódica. Uma diferença é que \(\tan x\) tem descontinuidades. Confira:

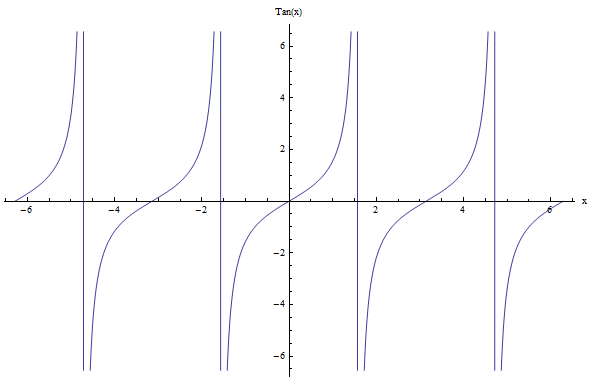
Da mesma forma que antes, a função cotangente \(\cot x\) é o inverso de \(\tan x\), com \(\cot x = \frac{1}{\tan x}\), então o período de \(\cot x\) também é \(\pi\).

Cálculo da frequência

Outro elemento importante a considerar para a função periódica é a frequência (\(f\)), que é calculada em termos do período \(P\) como:

\[f = \frac{1}{P}\]

Portanto, a frequência é o inverso do período. E vice-versa, o período é o inverso da frequência.

Por exemplo, qual é a frequência de \(\sin x\)? Seguindo a fórmula acima, pois sabemos que para seno o período é \(P = 2\pi\):

\[f = \frac{1}{P} = \frac{1}{2\pi} \approx 0.1592\]

Esta calculadora também calculará a amplitude, deslocamento de fase e deslocamento vertical se a função for definida corretamente. Esses parâmetros determinam bastante o comportamento da função trigonométrica.

Se você precisa representar graficamente uma função trigonométrica, você deve usar este criador de gráficos trigonométricos .