Solventes Cálculo

Regra do quociente

Instruções: Use esta calculadora de Quotient Rule para encontrar a derivada da função envolvendo quocientes que você fornecer, mostrando todas as etapas. Por favor, digite a função na caixa de formulário abaixo.

A regra do quociente

Esta calculadora permitirá que você use a Regra do Quociente para uma função que envolve um quociente, mostrando todas as etapas do processo. Tudo o que você precisa fornecer é uma função diferenciável válida. Essa função precisa envolver pelo menos um quociente para que a regra do quociente seja aplicável.

Um exemplo de uma função válida seria f(x) = (x^2 + 2x + 1)/(x^2-1), ou algo como f(x) = sin(x)/x, etc.

Uma vez fornecida uma função válida envolvendo quocientes, você deve clicar no botão "Calcular" para obter as etapas do cálculo mostradas.

Juntamente com o Regra Do Produto e Regra Da Cadeia , o Regra Do Quociente é um dos fundamentos mais importantes Regras de Derivadas .

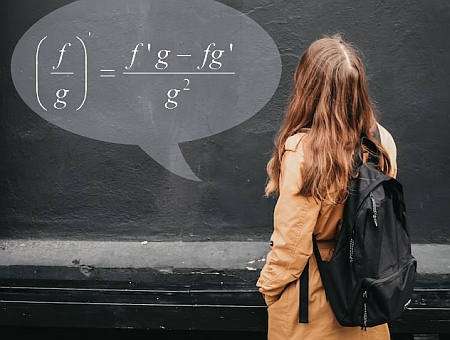
Fórmula da regra do quociente

Em termos simples, o Regra Do Quociente ajuda você a calcular a derivada de um quociente, usando o conhecimento das funções individuais e suas derivadas. A fórmula da regra do quociente é:

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

Quais são as etapas para usar a regra do quociente?

Passo 1: Identifique claramente as funções f(x) eg(x) que vão no numerador e no denominador do quociente
Passo 2: Simplifique qualquer termo óbvio que possa ser simplificado
Passo 3: Calcule as derivadas correspondentes f'(x) e g'(x)
Passo 4: Substitua os valores encontrados no Passo 3 na fórmula \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)

Observe que f(x) e g(x) ainda podem ser funções complexas, então você pode precisar usar outras regras como a regra da cadeia para calcular tanto f'(x) quanto g'(x).

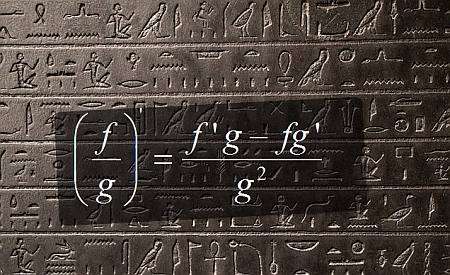
Derivada da regra do quociente

Ao calcular uma derivada de regra de quociente, você está reduzindo a derivada de um quociente ao conhecimento das derivadas individuais, mas essas derivadas individuais ainda podem exigir muitas etapas com Regras básicas de derivadas para ser resolvido.

É por isso que a diferenciação é considerada uma operação 'simples', mas, ainda assim, você precisa organizar suficientemente e acompanhar todas as partes que surgem ao decompor com regras de derivação e, em seguida, prosseguir com as partes menores que podem exigir mais regras de diferenciação para serem aplicado.

Portanto, você pode acabar com um processo iterativo, mas é garantido que ele terminará em algum ponto ao se aprofundar em cada parte menor, até encontrar uma derivada elementar, como polinomial ou um derivada trigonométrica .

Regra do quociente na diferenciação

O papel do regra do quociente na diferenciação é muito importante, uma boa razão pela qual você vai querer usar uma calculadora para isso. Em termos algébricos, a regra do quociente pode ser considerada mais complicada do que a regra do produto, e pode ser verdade em muitos casos, mas ainda depende da complexidade das funções no numerador e no denominador.

Exemplos de regra de quociente

Considere a função: \(f(x) = \frac{x^2+1}{x-2}\), encontre sua derivada.

Solução: Para este exemplo, precisamos analisar a função \(\displaystyle f(x)=\frac{x^2+1}{x-2}\), em termos de encontrar sua derivada.

\( \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)\)

By using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\) and \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}\)

Since the derivative of a constant is 0, we get that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Note that \((2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Removing unnecessary parentheses and multiplying the terms by \(-1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}\)

Aggregating those terms with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}\)

Putting together the numerical values and operating the terms that were grouped with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}\)

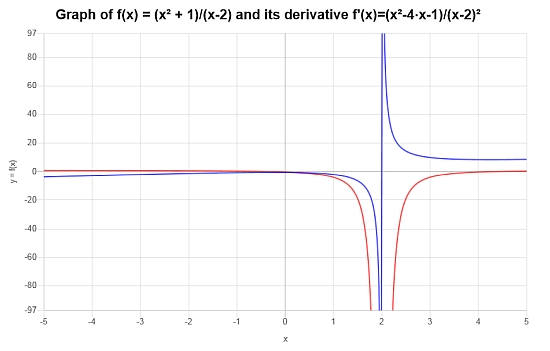
Conclusão : Descobrimos que a derivada da função dada é:

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

Então, a representação gráfica da função e sua derivada é \([-5, 5]\):

Exemplo: cálculo da regra do quociente

Agora considere \(f(x) = \frac{x}{\sin(x)}\), encontre sua derivada usando a Regra do Quociente.

Solução: Para este segundo exemplo, a função que nos interessa é \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\). Vamos diferenciá-lo usando a Regra do Quociente.

\( \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}\)

so then we get that

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}\)

By reorganizing/simplifying/expanding the terms that are amenable to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

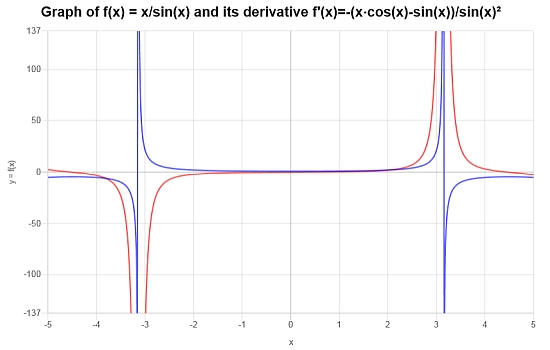
Conclusão : A conclusão é que, com base no cálculo acima, a derivada é dada por:

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

Graficamente, podemos ver a função (em azul) e sua derivada (em vermelho):

Mais exemplos de regra de quociente

Finalmente, considere a função: \(f(x) = \frac{\sin(x)}{x^2}\), encontre sua derivada.

Solução: Para este exemplo final da regra do quociente, trabalhamos com a função \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\). .

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)\)

The Quotient Rule applies: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

We use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}\)

By simplifying and regrouping terms

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\)

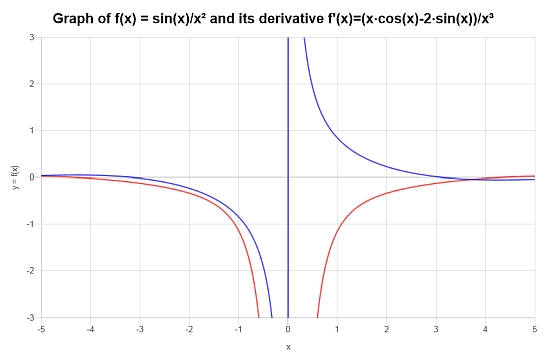
Conclusão : Para a função dada, sua derivada é:

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

O gráfico abaixo mostra a situação para \(f\) e \(f'\):

Mais calculadoras derivadas

Em Cálculo você vai encontrar derivados em todos os lugares que você olha. São milhares de aplicações envolvendo-os tornando-os as ferramentas mais importantes para Ciência e Engenharia.

Você precisará aprender sobre diferenciação implícita para diferentes aplicações muitas vezes envolvendo taxas relacionadas, ou em cálculo multivariado que você estará interessado encontrando derivadas parciais .

No geral, você achará sua vida mais fácil ao lidar com derivativos se for capaz de lidar adequadamente com os mais comuns. Regras de Derivadas , incluindo o Regra Da Cadeia , bem como o Regra Do Produto e Regra Do Quociente .