Calculadora de aproximação linear

Esse calculadora de linearização permitirá calcular a aproximação linear, também conhecida como Linha tangente para qualquer função válida dada, em um ponto válido dado.

Você precisa fornecer uma função válida como, por exemplo, f(x) = x*sin(x), ou f(x) = x^2 - 2x + 1, ou qualquer função válida que seja diferenciável e um ponto \(x_0\) onde a função está bem definida. Este ponto pode ser qualquer expressão numérica válida, como 1/3, por exemplo.

Depois de fornecer uma função e um ponto válidos, clique em "Calcular" e todos os cálculos serão mostrados para você.

Aproximação linear ou de primeira ordem procura uma aproximação da função dada por uma linha, em um dado ponto \(x_0\). Naturalmente, para curvas, uma aproximação linear será grosseira, embora a ideia principal seja que a aproximação seja precisa para pontos próximos a \(x_0\).

Aproximação linear

A ideia é encontrar uma reta que passe pelo ponto \((x_0, f(x_0))\) e "quase não toque" na função \(f(x)\). A definição matemática formal de 'mal tocando' é dada pela ideia de Linha tangente , para o qual precisamos Calcular para derivada da função.

De fato, a fórmula da aproximação linear no ponto \(x_0\) depende da derivada \(f'(x_0)\), como segue

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Esse fórmula de aproximação linear essencialmente define o equação de uma linha que passa pelo ponto \((x_0, f(x_0))\), por isso é chamada de "aproximação linear", pois define uma função linear que coincide com \(f(x)\) no ponto \(x_0\), e é muito próxima de \(f(x)\) para valores de \(x\) que estão próximos de \(x_0\).

Etapas para encontrar a aproximação linear

• Passo 1: Você precisa ter uma dada função f(x) e um ponto x0. A função deve ser diferenciável em x0
• Passo 2: Calcule f(x0) e f'(x0), que são a função e a derivada da função f no ponto x0
• Estágio 3: Defina a aproximação linear como y = f(x_0) + f'(x_0) (x - x_0), que é a fórmula de linearização apresentada acima

Esta linha, \(y = f(x_0) + f'(x_0) (x - x_0)\) representa a aproximação de primeira ordem, também conhecida como aproximação linear local.

Link com linha tangente

Como você provavelmente já deve ter suspeitado, a aproximação linear é a mesma que a Linha tangente no ponto dado. Então, calcular a aproximação linear é exatamente o mesmo que calcular a reta tangente

Outro nome para o mesmo é aproximação de primeira ordem, ou aproximação de linha tangente, que também são nomes comumente usados em Cálculo.

Aproximação diferencial e linear

Outro conceito comum é o de diferencial, que está intimamente ligado ao de aproximação linear, sendo simplesmente uma derivação dele. De fato, a diferencial (ou diferença finita) é definida como \(\Delta y = y - f(x_0)\). Então, com base na fórmula de aproximação de primeira ordem, a fórmula para o diferencial é

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

Isso naturalmente se parece exatamente com a fórmula de aproximação linear, exceto que o termo \(f(x_0\) é passado para a esquerda.

Exemplo: cálculo de aproximação de primeira ordem.

Considere o seguinte: \(f(x) = x^2 - 2x + 3\), encontre sua aproximação de primeira ordem em \(x_0 = 1\).

Solução: A função fornecida é \(\displaystyle f(x)=x^2-2x+3\), e precisamos encontrar a aproximação linear em torno do ponto x = 1. Então, primeiro precisamos da derivada.

Aproximação Linear : A equação da aproximação linear que procuramos no ponto \(x_0 = 2\) é dada pela seguinte fórmula

\[y = y_0 + f'(x_0)(x - x_0) \]

Observe que por definição \(\displaystyle y_0 = f(x_0)\), o que implica que precisamos plugar a função no ponto \(x_0 = 2\) :

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

Fazemos o mesmo, mas agora para a derivada no ponto \(x_0 = 2\), então

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

Agora com isso, voltamos à fórmula de aproximação linear:

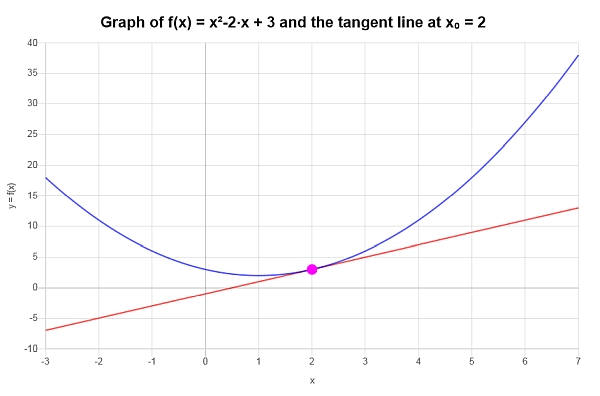
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

Conclusão : Concluímos que a aproximação linear para \(\displaystyle f(x)=x^2-2x+3\) em \(x_0 = 2\) é dada por:

\[y = 2x-1 \]

Graficamente:

Exemplo: mais aproximação de primeira ordem

Para a função : \(f(x) = x \sin(x)\) e o ponto \(x_0 = 2\), encontre a aproximação de primeira ordem correspondente.

Solução: Neste caso, a função que precisamos trabalhar é: \(\displaystyle f(x)=x\sin\left(x\right)\).

Agora calculamos sua derivada:

Aproximação Linear : A equação da aproximação linear é:

\[y = y_0 + f'(x_0)(x - x_0) \]

onde \(\displaystyle y_0 = f(x_0)\), então calculamos:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

Para a derivada em \(x_0 = 2\) descobrimos que:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

Agora estamos prontos para colocá-los de volta na fórmula de aproximação de primeira ordem:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Conclusão : Conclui-se que a aproximação linear de \(\displaystyle f(x)=x\sin\left(x\right)\) no ponto dado \(x_0 = 2\) é calculada como:

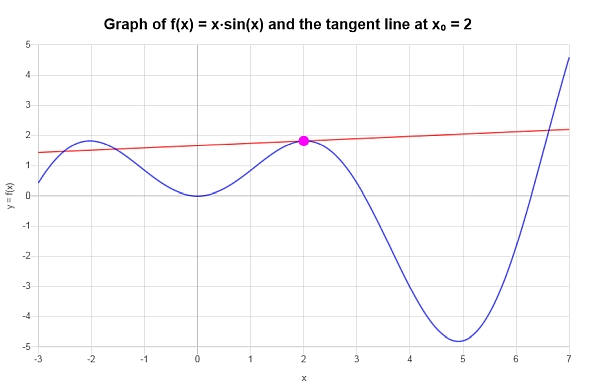
\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Graficamente, obtemos o seguinte gráfico:

Exemplo: cálculo de aproximação linear

Calcule a aproximação de primeira ordem para \( f(x) = \frac{\sin(x)}{x}\) em \(x = \frac{\pi}{4}\).

Solução: A seguinte função foi fornecida: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), para a qual precisamos calcular sua derivada.

A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada:

Aproximação De Primeira Ordem : A equação para a aproximação de primeira ordem correspondente para a função dada \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) no ponto dado \(x_0 = \frac{\pi}{4}\) é dada pelo seguinte:

\[y = y_0 + f'(x_0)(x - x_0) \]

Conectando os valores correspondentes:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

Então agora podemos colocar isso na fórmula:

\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Conclusão : Podemos concluir, portanto, que a aproximação de primeira ordem para a função dada \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) no ponto dado \(x_0 = \frac{\pi}{4}\) é dada por

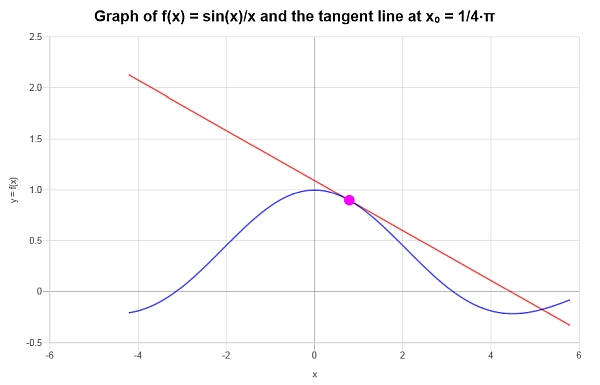
\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

O seguinte é obtido graficamente:

Mais calculadoras de derivadas

Além disso calculadora de linearização , você pode encontrar muitos que fazem coisas diferentes com base em derivativos. A diferenciação é uma operação crucial em Cálculo, Física, Engenharia e Economia, com um amplo espectro de aplicações.

Existe também uma forma de conduzir uma aproximação linear para mais variáveis, isto é, por exemplo, para uma função \f(x, y)\), caso em que a fórmula de aproximação linear se torna \(f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)\), então neste caso, para encontrar a linearização, precisamos usar derivadas parciais .

Encontrar a linearização de uma função não é de longe a única coisa que você pode fazer com derivadas. A diferenciação é uma operação relativamente fácil com regras simples como a Regra Do Produto , a regra do quociente e a Regra Da Cadeia que torna o cálculo de derivativos uma operação relativamente simples.

Embora deva ser simples, é uma boa ideia usar um calculadora derivada para obter todas as etapas mostradas, com uma menção clara de todos os Regras de Derivadas usado.