Sobre esta calculadora de linha tangente

Esta calculadora permitirá que você realize os cálculos necessários para obter a reta tangente de uma função, em um determinado ponto, mostrando todas as etapas.

Tudo o que você precisa fazer é fornecer uma função válida f(x) e um ponto onde deseja a linha tangente. A função pode ser qualquer função diferenciável válida como f(x) = sin(x) ou f(x) = x^2 - x + 1, etc. O ponto pode ser qualquer expressão numérica válida, como 1/2 para exemplo.

Então, quando as informações necessárias forem fornecidas e forem válidas, você precisará clicar em "Calcular" para obter todas as etapas da equação da reta tangente mostradas a você.

Aplicações de linha tangente são abundantes na ciência ao redor. Também chamado primeira ordem ou aproximação linear , tem um significado muito profundo em Física e Engenharia, onde a ideia da principal contribuição para a mudança (a parte de primeira ordem) é aquela que revela muitas informações sobre um processo.

Qual é a reta tangente

Em termos simples, uma linha tangente é uma linha que intercepta uma curva, mas a intercepta em apenas um ponto (pelo menos localmente). Esta linha tangente é construída fixando um ponto \(x_0\) e tomando um ponto diferente \(x_1\).

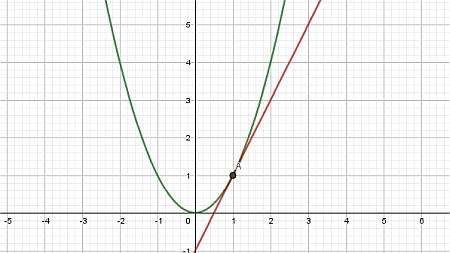
Então, construindo a reta que passa pelos pontos \((x_0, f(x_0))\) e \((x_1, f(x_1))\), obtemos o que chamamos de Linha Secante , conforme o gráfico abaixo:

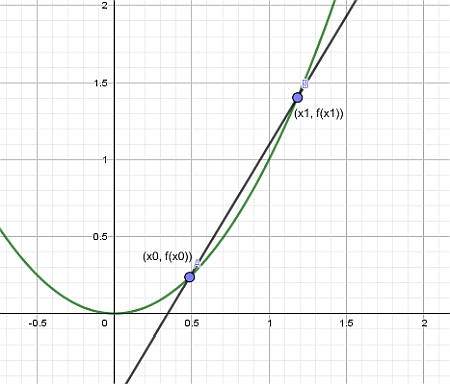
Finalmente, deixamos o ponto \(x_1\) se aproximar de \(x_0\), e o que obtemos é a reta tangente:

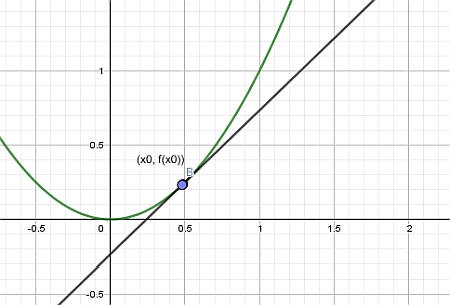
Etapas para encontrar a linha tangente geometricamente

• Passo 1: Identifique a função f(x) com a qual deseja trabalhar e o ponto x0. Você precisa dos dois
• Passo 2: O ponto (x0, f(x0)) estará na curva da função f(x). Plote isso
• Estágio 3: Escolha um ponto (x1, f(x1)), para um x1 diferente de x0 (pode estar à esquerda ou à direita de x). Plote isso
• Passo 4: Desenhe uma linha passando pelos pontos (x0, f(x0)) e (x1, f(x1))
• Passo 5: Escolha um ponto x2 que esteja a meio caminho entre x0 e x1 e desenhe uma linha passando pelos pontos (x0, f(x0)) e (x2, f(x2))
• Passo 6: Repita este processo algumas vezes

Este método gráfico ajudará você a ter uma ideia aproximada de como a linha tangente se parece, mas é uma aproximação (a menos que a função f(x) seja linear).

Fórmula da linha tangente

O método de aproximação usando linhas secantes pode dar uma ideia do que você está procurando, mas felizmente existe uma fórmula exata para calcular a linha tangente a uma função em um ponto \(x_0\). A fórmula da reta tangente é:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Simples, né? Em termos simples, esta fórmula está dizendo que a linha tangente é um linha que passa pelo ponto \((x_0, f(x_0))\) e que tem uma inclinação de \(m = f'(x_0)\)

Então, em termos simples, a inclinação da reta tangente em um determinado ponto é exatamente a derivada da função naquele ponto.

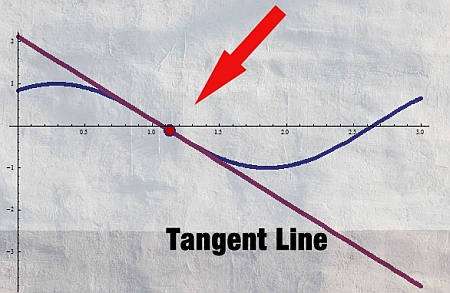
Etapas para aplicar a fórmula da linha tangente

• Passo 1: Identifique a função f(x) e o ponto x0
• Passo 2: Calcule o valor da função em x0, que é f(x0)
• Estágio 3: Calcule a derivada de f(x) no ponto x0, então você precisa de f'(x0)
• Passo 4: Aplique diretamente a fórmula da reta tangente \(y = f(x_0) + f'(x_0) (x - x_0)\)

Assim que tiver o equação da linha , você pode transformá-lo no formato que for mais útil para a situação em questão.

A inclinação da reta tangente

Uma das principais conclusões é que a inclinação da linha tangente em \(x_0\) é exatamente \(f'(x_0)\), que é a derivada no ponto \(x_0\). Isso fornece uma interpretação clara e extremamente útil da derivada em termos geométricos.

Esta conexão permite encontrar a equação da reta tangente a uma determinada curva em um determinado ponto simplesmente olhando para a derivada da função.

Quando você tem uma linha tangente horizontal?

Uma linha tangente horizontal ocorrerá quando o ponto escolhido \(x_0\) quando a derivada correspondente naquele ponto for igual a zero. Nesse caso, a linha tangente (que é a linha que toca a curva em um ponto localmente) será paralela ao eixo y.

Então, tudo que você precisa saber para identificar retas tangentes horizontais é encontrar pontos onde a derivada da função é zero.

Quando você tem uma linha tangente vertical?

Uma linha tangente vertical ocorrerá quando a derivada for "infinita" em um ponto. Essa é uma forma simples de dizer que é onde a derivada não está definida em um determinado ponto, mas converge para o infinito conforme nos aproximamos do ponto.

Por exemplo, pode-se dizer que \(f(x) = \frac{1}{x}\) tem uma reta tangente vertical em x = 0. No entanto, pode-se argumentar que não há reta tangente porque a derivada não está bem definida em x = 0.

Exemplo: linha tangente

Encontre a equação da reta tangente para \(f(x) = x^2 - 2x + 1\), no ponto \(x_0 = 2\).

Solução: A seguinte função é aquela com a qual precisamos trabalhar: \(\displaystyle f(x)=x^2-2x+1\). Primeiro, precisamos calcular sua derivada.

A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada:

Linha Tangente : A equação da reta tangente para a função \(\displaystyle f(x)=x^2-2x+1\) no ponto \(x_0 = 2\) é:

\[y = y_0 + f'(x_0)(x - x_0) \]

Neste caso, \(\displaystyle y_0 = f(x_0)\), então inserir o valor do ponto \(x_0 = 2\) na função leva a:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

Além disso, inserir o valor do ponto \(x_0 = 2\) na derivada calculada leva a:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

Então, agora inserimos esses valores na fórmula da linha tangente para obter:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

Conclusão : Portanto, verifica-se que a reta tangente para a função \(\displaystyle f(x)=x^2-2x+1\) no ponto \(x_0 = 2\) é:

\[y = 2x-3 \]

O gráfico a seguir é obtido para a função dada e sua reta tangente em \(x_0 = 2\):

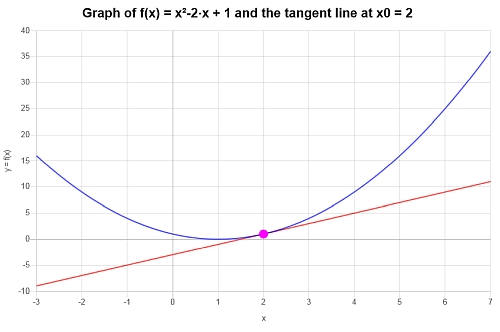
Exemplo: equação da reta tangente

Qual é a reta tangente em x = 1/2, para a função \(f(x) = \sin(x) + 1\)?

Solução:

A seguinte função foi fornecida: \(\displaystyle f(x)=\sin\left(x\right)+1\), para a qual precisamos calcular sua derivada.

A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada:

Linha Tangente : Descobrimos que a equação correspondente da reta tangente no ponto \(x_0 = \frac{1}{2}\) é dada por:

\[y = y_0 + f'(x_0)(x - x_0) \]

Mas neste caso específico, \(\displaystyle y_0 = f(x_0)\), o que significa que precisamos inserir o valor do ponto \(x_0 = \frac{1}{2}\) na função, então obtemos:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

Agora, fazendo o mesmo na derivada, para \(x_0 = \frac{1}{2}\) encontramos

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

Agora só precisamos inserir os valores, então descobrimos que

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Conclusão : Descobrimos que a linha tangente correspondente que estamos procurando, no ponto correspondente \(x_0 = \frac{1}{2}\) é dada por

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Graficamente:

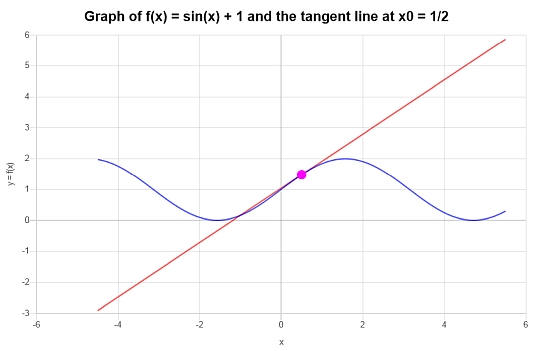
Exemplo: outra reta tangente

Qual é a reta tangente em x = 0, para a função \(f(x) = \cos(x)\)? Esse resultado faz sentido?

Solução: Observe que \(f'(x) = -\sin(x)\), então \(f'(0) = -\sin(0) = 0\). Isto é, a reta tangente tem uma inclinação de m = 0 em x = 0, então a equação da reta tangente é simplesmente \(y = y_0 = \cos(0) = 1\). Isso faz sentido porque, nesse caso, a linha tangente é uma linha horizontal.

Mais calculadoras de diferenciação

Algumas pessoas podem afirmar que a diferenciação é um exercício relativamente simples e que o uso de uma calculadora derivada pode não ser necessário, mas, na verdade, o cálculo de derivadas ainda pode ser bastante complicado e pode exigir longos cálculos algébricos .

Quando você tem uma expressão com mais de uma variável, para encontrar a derivada você precisará determinar se as variáveis são independentes umas das outras, caso em que você usa derivadas parciais , ou se houver uma equação que vincule as variáveis, caso em que você precisaria usar diferenciação implícita .

As duas principais áreas do cálculo diferencial são integração e diferenciação, e ambas têm suas amplas aplicações em todos os lugares. derivadas parciais aparecem em grande extensão em aplicações de Engenharia e Economia.

Por um lado, a diferenciação lida com taxas infinitesimais de mudança, enquanto a integração lida com a soma de taxas infinitesimais de mudança e, admiravelmente, elas estão fortemente ligadas pela Teorema Fundamental do Cálculo .