Solventes Cálculo

Regras de derivadas

Instruções: Use esta calculadora de derivadas para encontrar a derivada de qualquer função que você fornecer, usando as regras de derivadas mais comuns, mostrando todas as etapas. Por favor, digite a função que você deseja aplicar regras derivadas na caixa de formulário abaixo.

Sobre regras de derivadas

Esta calculadora permitirá que você calcule a derivada de uma função fornecida aplicando as regras básicas de diferenciação necessárias, mostrando todas as etapas do processo e observando onde cada regra é aplicada.

Você só precisa fornecer uma função válida que seja diferenciável (o que significa que ela possui uma derivada). Por exemplo, uma função válida pode ser f(x) = 1/3*x*sin(x), apenas para citar um exemplo.

Depois, quando você já tiver digitado sua função, basta clicar em "Calcular" para obter todas as etapas da diferenciação mostradas.

A simplicidade das regras de derivativos torna o processo de diferenciação reconhecido como "fácil", um julgamento que talvez seja um exagero.

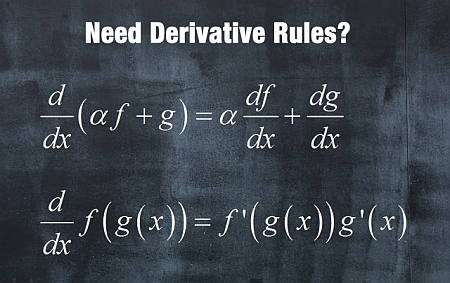
Regras básicas de derivadas

Existem quatro regras básicas de derivadas para você aprender

Regra De Linearidade: Para funções \(f(x)\) e \(g(x)\), e uma constante \(a\), então a derivada é uma operação linear: \((af(x)+g(x))' = af'(x)+g'(x)\)
Regra Do Produto Para as funções \(f(x)\) e \(g(x)\), a derivada do produto é \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)
Regra Do Quociente: Para as funções \(f(x)\) e \(g(x)\), a derivada do quociente é \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
Regra Da Cadeia Para as funções \(f(x)\) e \(g(x)\), a derivada da função composta é \((f(g(x)))' = f'(g(x))g'(x)\)

Essas regras funcionarão como um encanto e ajudarão você a encontrar a derivada de qualquer função básica.

Como usar as regras de derivadas?

Passo 1: Identifique a função f(x) que você deseja diferenciar, simplifique se necessário
Passo 2: Tente dividir a função em partes derivadas menores, usando linearidade
Passo 3: Dependendo da estrutura da função f(x), use qualquer uma das regras disponíveis (produto, quociente e regra da cadeia) e esteja ciente de que pode ser necessário aplicar muitas das regras consecutivamente)

Normalmente, você terminará com uma combinação de várias regras de diferenciação, até chegar ao ponto em que encontrará uma função elementar, da qual você já sabe diferenciar.

Posso resolver todas as derivadas

Dizer que usar regras de diferenciação pode levar você a resolver TODAS as derivadas pode ser um exagero. Você será capaz de resolver A MAIORIA das derivadas, e certamente todas as básicas, mas existem funções que têm um comportamento menos intuitivo que poderia ser definido, embora não sejam tipicamente tratadas em cursos básicos de Cálculo.

No que diz respeito às funções básicas, a maioria delas será diferenciada sem problemas.

Uma derivada da regra do produto , derivada da regra do quociente ou derivada da regra da cadeia provavelmente não estarão isoladas e provavelmente virão em uma sequência de várias regras que precisam ser usadas juntas.

Exemplo: regras de derivadas

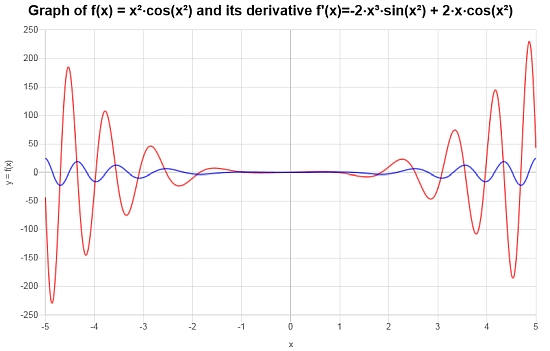
Usando regras básicas de derivadas, calcule a seguinte derivada: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)

Solução: Vamos considerar a seguinte função dada para a qual a derivada precisa ser calculada \(\displaystyle f(x)=x^2\cos\left(x^2\right)\)

A função não precisa de simplificação, então podemos ir direto ao cálculo de sua derivada:

\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)

Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)

so then we get

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)

And finally, grouping the terms together

\( \displaystyle = \,\,\)

\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)

O gráfico correspondente da função e sua derivada é mostrado abaixo:

Exemplo: regras mais derivadas

Calcule a seguinte derivada: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\) usando regras básicas de derivadas.

Solução: Agora, a tarefa em questão é derivar a função \(\displaystyle f(x)=x\cos\left(x^2+1\right)\)

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)

In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)

Exemplo de regras derivadas

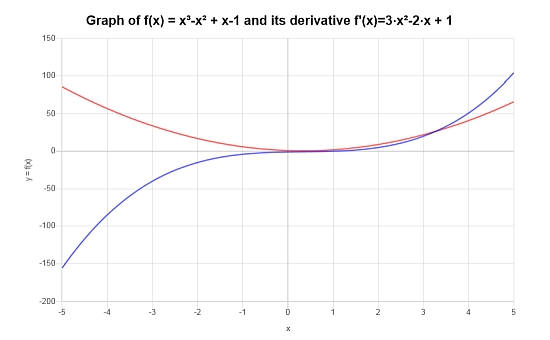
Para a função \( f(x) = (x-1)(x^2+1) \), use as regras de derivação para encontrar sua derivada.

Solução: Para este exemplo final, precisamos diferenciar: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\).

Estado Inicial: Nesse caso, primeiro precisamos expandir a função dada \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \) e, para isso, realizamos as seguintes etapas de simplificação:

\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)

Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-x^2+x-1\)

Depois de expandir a função, podemos proceder ao cálculo da derivada:

\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2-2x+1\)

Graficamente, é assim que a função e sua derivada se parecem:

Mais calculadoras derivadas

Uma das mágicas da diferenciação é que você pode encontre a derivada de qualquer função usando algumas regras básicas e simples, incluindo o Regra Do Produto , Regra Do Quociente e naturalmente, a regra da cadeia . Este pequeno arsenal geralmente é suficiente para calcular qualquer derivada que você precise.

Diferenciação e integração são as principais vias do Cálculo, indiscutivelmente, pois são o centro de tantas aplicações, em todos os aspectos da ciência. De taxas relacionadas a diferenciação implícita , com derivadas parciais em Física e Economia