Diferenciação implícita

Esta calculadora o ajudará a conduzir a diferenciação implícita para uma equação que envolve as variáveis x e y. Você precisa fornecer uma equação válida como x^2 + y^2 = 1, ou xy - x^2 y^2 = 0, etc.

Depois de fornecer uma equação válida envolvendo duas variáveis (\(x\) e \(y\)), basta clicar no botão "Calcular" e serão mostrados todos os passos da diferenciação implícita correspondente.

Isto é um calculadora dy/dx com passos no sentido de que irá mostrar todas as etapas relevantes do cálculo da derivada de uma variável em relação a outra, desde que essas duas variáveis estão relacionadas em uma equação. Esta relação é o que permite encontrar o correspondente derivada implícita .

Ter uma equação que relacione as duas variáveis \(x\) e \(y\) nos diz que devemos ser capazes de expressar \(y\) como uma função de \(x\) e escrever \(y = y(x)\). Freqüentemente, não podemos expressar explicitamente \(y\) como uma função de \(x\), assumimos que existe tal função; nesse caso, faz sentido diferenciar \(y\) em relação a \(x\).

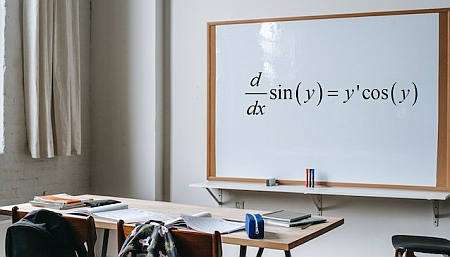
O que é diferenciação implícita?

A diferenciação implícita é uma cálculo de diferenciação técnica baseada na suposição de que é possível afirmar a partir de uma dada equação envolvendo \(x\) e \(y\) que \(y\) é uma função de \(x\) embora muitas vezes não possamos escrever explicitamente tal função.

Uma vez feita essa suposição, assumimos que podemos calcular \(\frac{dy}{dx}\) e podemos usar todos os valores conhecidos Regras de Derivadas ( Regra Do Produto , Regra Do Quociente e Regra Da Cadeia ) para diferenciar ambos os lados da equação e resolver \(\frac{dy}{dx}\).

Qual é o método de diferenciação implícita?

O método de diferenciação implícita é um método que permite calcular uma derivada para expressões que não são colocadas diretamente no formato \(f(x)\). Isto é, quando dada uma função de uma variável \(x\) por exemplo, simplesmente seguimos em frente e diferenciamos essa função.

Mas quando duas variáveis \(x\) e \(y\) estão relacionadas através de uma equação, como \(x^2+y^2 = 1\) por exemplo, você também pode diferenciar y em relação a x, no método tradicional, você precisará RESOLVER y em termos de x, e ENTÃO você pode diferenciar.

Usando a diferenciação implícita, você pode diferenciar diretamente, apenas supondo que \(y = y(x\) e fazendo uso do Regra Da Cadeia .

Etapas para usar a diferenciação implícita

• Passo 1: Identifique a equação que envolve duas variáveis x e y. Simplifique quaisquer termos redundantes
• Passo 2: Assuma que y é uma função de x, y = y(x), então faz sentido calcular a derivada de y em relação a x
• Estágio 3: Calcular para derivada de ambos os lados da equação usando todos os Regras de Derivadas você precisa. Isso levará a uma igualdade na qual x, y e y' estão potencialmente presentes
• Passo 4: Resolva o que você obteve na Etapa 3 para y'. Observe que y' geralmente será escrito como uma função de x e y, o que é bom, pois y também depende de x

Esta é uma metodologia muito geral e terá sutilezas de caso para caso, mas esse é o esquema que deve funcionar na maioria dos casos, com a potencial dificuldade adicional de manipulações algébricas.

Por que usar uma calculadora de diferenciação implícita

A diferenciação implícita pode ser confusa às vezes, se você não for muito claro sobre o que está diferenciando e em relação a qual variável. Uma calculadora irá ajudá-lo a comparar seu resultado e uma coisa especial sobre nossa calculadora é que todas as etapas do processo são mostradas.

Essa é uma ajuda crucial para você, porque mostrará exatamente qual regra de derivada e onde você a aplicou.

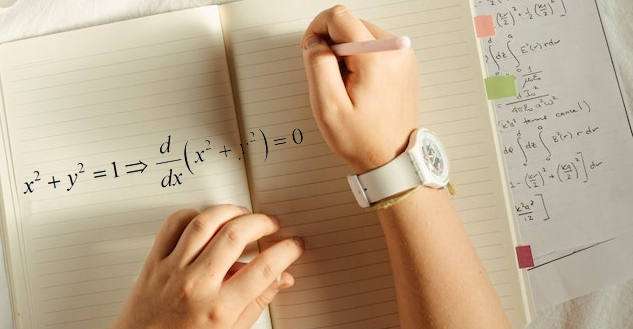
Qual é o ponto de diferenciação implícita?

Essa é uma pergunta justa. Se você tem uma equação envolvendo x e y, por que não resolver y em termos de x e usar o cálculo de derivada regular para obter a derivada de y em relação a x. Posso dar-lhe pelo menos duas boas razões:

• Motivo 1: Pode ser que você NÃO POSSA resolver y em termos de x explicitamente. Pode haver uma função, mas você não pode simplesmente encontrá-la. Pense em y + tan(y) = x^2
• Motivo 2: Mesmo que por acaso você resolva y em termo de x , pode ser uma expressão realmente complicada e o cálculo da derivada pode ser muito complicado e difícil. Normalmente, a diferenciação implícita é algebricamente simples, em termos relativos

A derivada implícita depende de y?

Nem sempre, mas frequentemente. Agora, isso apenas diz que \(\frac{dy}{dx}\) pode depender de x e y, mas como y depende de x, está apenas dizendo que, como esperado, \(\frac{dy}{dx}\) depende de x.

Diferentes exemplos de diferenciação implícita serão apresentados na seção seguinte.

Segunda derivada implícita

Uma questão é: é possível calcular a segunda derivada usando diferenciação implícita? A resposta é sim. Você apenas faz o mesmo que com a primeira derivada usando diferenciação implícita, simplesmente assume que \(y\) é uma função de \(x\), então você escreve \(y = y(x)\) e pode derivar o quanto desejar.

Por exemplo, digamos que você queira encontrar \(\frac{d^2y}{dx^2}\) dada a equação \(x^2+y^2=1\). Diferenciando ambos os lados em relação a \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Agora, você deriva novamente em relação a x:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

e agora resolvemos para \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Exemplo: exemplo de diferenciação implícita

Encontre \(\frac{dy}{dx}\) para a equação: \(x^2 - y^2 = 2y\)

Solução: Este é um exemplo de diferenciação implícita. A seguinte equação foi fornecida: \(\displaystyle x^2-y^2=2y\), para a qual precisamos conduzir uma diferenciação implícita, onde assumimos que \(y\) é uma função de \(x\) .

A equação não precisa de mais simplificação, então podemos prosseguir com a diferenciação implícita:

Precisamos diferenciar ambos os lados da equação em relação a \(x\), e em ambos os lados assumimos que \(y = y(x)\).

Lado esquerdo : Diferenciando o lado esquerdo em relação a \(x\)

Lado direito : Diferenciando o lado direito em relação a \(x\)

Portanto, após diferenciar ambos os lados em relação a \(x\), obtém-se o seguinte:

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Colocando todos os termos de um lado:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Agrupando tudo que contém \(\displaystyle \frac{dy}{dx}\):

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Finalmente, resolvendo para \(\displaystyle \frac{dy}{dx}\), leva a:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Exemplo: cálculos de diferenciação mais implícita

Qual é a inclinação da reta tangente a um círculo unitário no ponto \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)

Solução: Observe que a equação do círculo unitário é \(\displaystyle x^2 + y^2 = 1\), que define implicitamente \(y\) como uma função de \(x\). Para encontrar a reta tangente, precisamos calcular \(\frac{dy}{dx}\) no ponto especificado. Usando diferenciação implícita, diferenciamos ambos os lados da equação que define o círculo unitário: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

O ponto de interesse é \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), então .

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Isto implica que a inclinação da reta tangente no ponto \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) é \(m = -1\), o que implica que a equação da reta tangente naquele ponto é

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Exemplo de diferenciação implícita

Considere a equação: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Calcular \(\frac{dy}{dx}\)

Solução: Neste caso temos a seguinte equação: \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), então precisamos fazer diferenciação implícita, partindo do pressuposto de que \(y\) depende de\(x\) .

Não é necessária uma simplificação adicional da equação, o que nos permite prosseguir com a diferenciação implícita:

Agora precisamos calcular a derivada de ambos os lados em relação à variável \(x\), assumindo que \(y = y(x)\).

Lado esquerdo : Diferenciando o lado esquerdo em relação à variável \(x\)

Lado direito : Agora diferenciamos o lado direito em relação a \(x\)

Portanto, o resultado obtido após diferenciar ambos os lados em relação a \(x\) é:

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

Portanto, agora podemos resolver \(\displaystyle \frac{dy}{dx}\) para obter:

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

Solucionadores de cálculo mais úteis

Uma das aplicações mais interessantes do regras de derivativos é o conceito de diferenciação implícita. Tem aplicações em Física, Economia e Engenharia, e é extremamente prático para descrever a taxa de variação ao longo de curvas.

Um tipo diferente de derivados são derivadas parciais em que, ao contrário do caso de diferenciação implícita em que assumimos que y = y(x), nesse caso y é considerado uma constante quando x muda.