Mais sobre desigualdades quadráticas

Este cálculo de desigualdade quadrática fornecerá soluções para desigualdades mostrando todas as etapas. Por exemplo, a desigualdade que você fornece pode ser algo como 'x^2 - 1/2 > 0' e, em geral, as desigualdades quadráticas não são muito difíceis de resolver.

Depois de fornecer uma desigualdade válida envolvendo expressão quadrática , você pode clicar em "Calcular" para obter todas as etapas do cálculo que lhe são mostradas, incluindo um gráfico das soluções da desigualdade.

desigualdades quadráticas são um dos poucos tipos (junto com desigualdades lineares ) que você terá a garantia de encontrar uma solução exata, e esse processo envolve a resolução de uma equação quadrática.

Qual é a definição deste tipo de desigualdade

Não o declaramos explicitamente, mas fica claro pelo seu nome: uma desigualdade quadrática é um tipo específico de desigualdade em que todos os termos envolvidos nela são polinômios de no máximo grau 2. Neste contexto, um exemplo é

\[\displaystyle x^2 < x - 1\]

que é quadrático pelo fato de que ambos os lados da desigualdade são polinômios de ordem no máximo 2. Agora, se você tivesse:

\[\displaystyle x^2 < x^3 - 1\]

então a desigualdade não é mais quadrática, por causa do termo \(x^3\) no lado direito. Para estas desigualdades temos um roteiro claro para encontrar a solução.

Passos para resolver desigualdades quadráticas

• Passo 1: Certifique-se de que possui uma desigualdade quadrática, pois o método utilizado neste caso é válido apenas para este tipo de desigualdade
• Passo 2: Tal como acontece com a maioria das desigualdades, passe tudo para o lado esquerdo da desigualdade e resolva a equação associada
• Estágio 3: Se a equação quadrática associada não tiver raízes reais, sabemos então que ou toda a reta real é uma solução ou não há solução. Então você testa qualquer ponto e vê se ele resolve a inequação, e se resolver, a solução é toda a reta real (-∞, ∞), caso contrário, a solução é vazia.
• Passo 4: Se a equação quadrática associada tiver apenas uma solução real, significa que o gráfico quadrático associado toca tangencialmente o eixo x. Portanto, dependendo do sinal de desigualdade, você pode ter apenas o ponto de contato sendo a solução, ou tudo, exceto o ponto de contato sendo a solução, ou toda a reta real (-∞, ∞), para a qual você precisa testar o ponto de contato, e um ponto fora dele (à esquerda e à direita do ponto)
• Passo 4: Se a equação quadrática associada tiver duas soluções reais diferentes, você verifica os intervalos definidos por essas raízes para determinar quais partes da reta real farão parte da solução

Ao analisar as peças, se necessário, você as une usando o operador "união", que é usado para juntar intervalos.

Como você desenha uma desigualdade quadrática?

Representando graficamente desigualdades fornece uma ótima maneira de entender visualmente a aparência da solução. Em termos de procedimento, você precisa saber se está trabalhando com uma desigualdade de uma variável ou se tem mais variáveis.

Se você tiver uma desigualdade como

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

você tem apenas uma variável e então a solução será um subconjunto da linha real. Por outro lado, se você tivesse algo como

\[\displaystyle y < x^2 - \frac{1}{2} x \]

então você terá apenas duas variáveis x e y, e então a solução da desigualdade será um subconjunto do plano xy.

Importância das expressões quadráticas

As expressões quadráticas envolvidas em equações e desigualdades desempenham um papel fundamental na Matemática. Talvez quadrática seja o tipo de estrutura mais amplamente utilizado depois da linear.

Ao lidar com Cálculo e Álgebra você encontrará inúmeras aplicações da quadrática em problemas de maximização e minimização, integração e muito mais. Pesquisando um pouco você encontrará aplicações de expressões quadráticas em diferentes disciplinas científicas

Exemplo: desigualdades quadráticas

Resolva esta desigualdade quadrática: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Solução:

Precisamos primeiro resolver a seguinte equação quadrática auxiliar \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\).

Aplicando a fórmula quadrática

A equação quadrática é:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Neste caso, temos:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

Colocando esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

então, descobrimos que:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Pontos críticos

A lista de pontos críticos encontrados organizados em ordem crescente é: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Então, precisamos analisar os seguintes intervalos críticos:

• Para o intervalo \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): O lado esquerdo é positivo, então \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) não faz parte da solução.

• Para o intervalo \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): O lado esquerdo é negativo, o que implica que \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) faz parte da solução.

• Para o intervalo \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\): O lado esquerdo é positivo, o que significa que \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) não faz parte da solução.

Solução

Com base na desigualdade fornecida e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Usando a notação de intervalo, a solução é escrita como:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]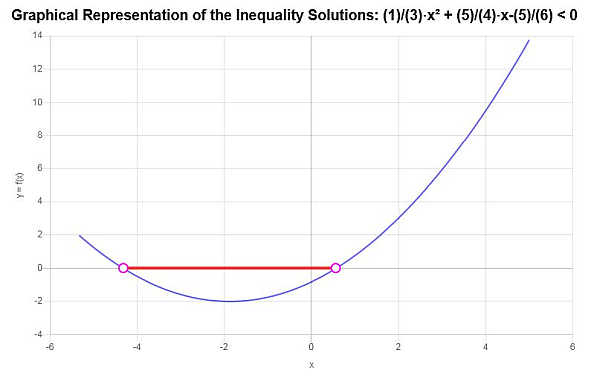

Exemplo: mais desigualdades quadráticas

Resolva: \(x^2 < 4\)

Solução:

A desigualdade dada é:

\[x^2 < 4\]

que deriva da equação quadrática \(\displaystyle x^2-4=0\).

Fórmula quadrática

Para uma equação quadrática da forma \(a x^2 + bx + c = 0\), as raízes são calculadas usando o seguinte Fórmula quadrática :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

Neste caso, temos que a equação que precisamos resolver é \(\displaystyle x^2-4 = 0\), o que implica que os coeficientes correspondentes são:

\[a = 1\] \[b = 0\] \[c = -4\]

Primeiro, calcularemos o discriminante para avaliar a natureza das raízes. A discriminação é calculada como:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Como neste caso obtemos o discriminante \(\Delta = \displaystyle 16 > 0\), que é positivo, sabemos que a equação tem duas raízes reais diferentes.

Agora, inserindo esses valores na fórmula das raízes, obtemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

então, descobrimos que:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

Neste caso, a equação quadrática \( \displaystyle x^2-4 = 0 \), possui duas raízes reais, então:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

então o polinômio original é fatorado como \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \), o que completa a fatoração.

Analisando pontos críticos

A lista de pontos críticos encontrados organizados em ordem crescente é: \(-2\), \(2\).

Com base nisso, precisamos analisar os seguintes intervalos:

• Para o intervalo \(\left(-\infty, -2\right)\): O lado esquerdo é positivo, então \(\left(-\infty, -2\right)\) não faz parte da solução.

• Para o intervalo \(\left(-2, 2\right)\): O lado esquerdo é negativo, então \(\left(-2, 2\right)\) faz parte da solução.

• Para o intervalo \(\left(2, \infty\right)\): O lado esquerdo é positivo, o que significa que \(\left(2, \infty\right)\) não faz parte da solução.

Solução para a desigualdade

Com base na desigualdade fornecida e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(-2< x \le 2\).

Usando a notação de intervalo, a solução é escrita como:

\[\left[-2,2\right)\]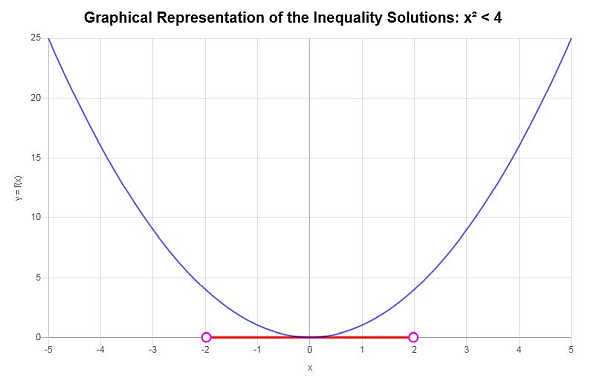

Outras calculadoras de desigualdade úteis

O tipo de desigualdade mais simples que você será capaz de resolver é desigualdades lineares . Depois disso, você tem desigualdades quadráticas, em termos de facilidade.

Então, você tem desigualdades polinomiais em geral, com grau superior a 2. Essas deveriam ser simples, mas ainda assim poderiam ser tarefas formidáveis em termos da quantidade de trabalho trabalhoso necessário para resolvê-las.

Tendo um calculadora de desigualdade para as desigualdades em geral pode realmente ser útil, pois abordará os diferentes tipos de desigualdades que são passíveis de procura de soluções exactas.