Calculadora de desigualdade
Instruções: Use a calculadora de desigualdade para resolver qualquer desigualdade fornecida, mostrando todas as etapas. Por favor, digite a desigualdade que deseja resolver na caixa abaixo:
Mais sobre como resolver desigualdades
Com esta calculadora você poderá resolver as desigualdades que fornece. Tudo o que você precisa fazer é digitar a desigualdade desejada na caixa e também certificar-se de que está fornecendo uma desigualdade válida.
Por exemplo, você pode fornecer algo como '2x^2 - x >= 1/2' ou algo como 'sin(x) > 0', desde que forneça valores válidos. Certifique-se também de usar um sinal de desigualdade, como ">", "<", ">=" ou "<=".
Se, em vez disso, você usar "=", esta calculadora funcionará como um calculadora de equação .
Depois de fornecer uma desigualdade válida, o próximo passo é clicar em “Resolver”, e em uma fração de segundo será apresentada a solução passo a passo. Uma advertência: nem todas as desigualdades poderão ser resolvidas, por isso tenha isso em mente.
Nem todas as desigualdades são fáceis de resolver, nem podemos aplicar alguns métodos pré-concebidos. Apenas alguns tipos, como desigualdades lineares , desigualdades quadráticas ou igualdades polinomiais (para graus inferiores) admitem um tratamento sistemático.

O que é uma desigualdade?
Uma desigualdade é um tipo de objeto matemático muito semelhante a um equação matemática , com a diferença de que em vez de "=", uma desigualdade contém ">", "<", ">=" ou "<=". Essa pequena diferença na aparência ainda acrescenta mais complexidade à resolução de uma inequação do que a uma equação.
Por exemplo, a expressão abaixo é uma desigualdade
\[\displaystyle x + \frac{1}{3} < x^2 \]Portanto, é uma expressão matemática que possui dois lados, o lado esquerdo e o lado direito, e tem “<” como sinal de desigualdade correspondente. A desigualdade acima é considerada uma desigualdade quadrática, porque as expressões nos lados esquerdo e direito são ambas polinomiais e o grau mais alto é 2.
Agora, por exemplo, a desigualdade abaixo é uma desigualdade trigonométrica:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]É uma desigualdade porque tem o sinal de desigualdade \(\le\), e o lado direito contém um expressão trigonométrica . Observe que a primeira desigualdade é bastante simples de resolver, enquanto a outra mão está longe de ser fácil e você realmente não consegue resolvê-la.
Como resolver uma desigualdade
Em termos gerais, encontraremos a solução para as desigualdades resolvendo primeiro uma equação associada. Resolver a desigualdade será mais difícil quando a equação associada for mais difícil de resolver. As etapas a seguir irão ajudá-lo no processo de solução:
- Etapa 0: Simplifique as expressões envolvidos na desigualdade. Quase sempre é mais fácil resolver uma desigualdade simplificada do que resolver a original
- Passo 1: Identifique a desigualdade que deseja resolver e identifique cuidadosamente o sinal da desigualdade (>, ≥, <, ≤). Se você tiver "=", você deve usar um calculadora de equação em vez de
- Passo 2: Você então escreve a equação associada, que é obtida simplesmente substituindo o sinal de desigualdade encontrado na etapa anterior e, em seguida, substituindo-o pelo sinal de igualdade "="
- Estágio 3: Resolva a equação associada. Você determinará a solução da inequação com base na existência de soluções reais para sua equação associada e tomando notas sobre quaisquer pontos que possam tornar a expressão indefinida
- Passo 4: Se a sua equação associada não tem solução real: Nesse caso, você sabe que a equação nunca é zero, pelo menos para valores reais. Então, e assumindo a continuidade, ou todos os pontos são solução da desigualdade ou nenhum o é. Então você avalia a desigualdade em qualquer ponto (digamos x = 0), e se ela for válida, então todos os valores reais são solução para a desigualdade, e se isso não acontecer, então não há soluções reais
- Etapa 5: Finalmente, suponha que existam soluções reais para a equação associada. Chamaremos esses pontos críticos e adicionaremos quaisquer pontos onde a expressão se torne indefinida (divisões por zero, etc.) à lista de pontos críticos
- Etapa 6: Se houver apenas um ponto crítico, que chamamos de 'a': Avalie a desigualdade em qualquer ponto à esquerda de 'a' e, se for válida, o intervalo (-∞, a) fará parte do conjunto solução. Se a desigualdade for "<=" ou ">=", então você inclui o ponto final. Finalmente, (-∞, a). Você dá um passo semelhante para um ponto à direita de 'a', e se a desigualdade for válida para ele, então (-∞, a) fará parte do conjunto solução
- Estágio 7: Um processo semelhante é realizado se existir mais de um ponto crítico: Tome dois pontos críticos consecutivos, que chamamos de 'a1' e 'a2': Avalie a desigualdade em qualquer ponto entre a1 e a2 e, se for válida, o intervalo ( a1, a2) farão parte do conjunto solução. Se a desigualdade for "<=" ou ">=", então você inclui os pontos finais
Parece complicado, mas basta ser sistemático. Por exemplo, se a sua desigualdade for \(\displaystyle x + \frac{1}{3} < x^2 \), então a equação associada é \(\displaystyle x + \frac{1}{3} = x^2 \), o que é fácil de resolver, pois é um Equação quadrática .
Então, no contexto da análise dos pontos críticos (se houver), traçando o gráfico da solução da desigualdade pode tornar as coisas mais claras. Em algumas aulas de Álgebra ensinam os alunos a usar uma tabulação para acompanhar o que acontece entre os pontos críticos, o que pode ser muito útil.
Qual é a diferença com um sistema de desigualdades?
Um sistema de desigualdades consiste em várias desigualdades simultâneas que precisam ser resolvidas ao mesmo tempo. Parece mais difícil do que resolver uma simples desigualdade porque é mais difícil. Se resolver desigualdades pode ser trabalhoso, ainda mais para sistemas de desigualdades.
Um exemplo de sistema de desigualdades é mostrado abaixo:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]No exemplo acima você tem um sistema de desigualdades para ser resolvido. Este sistema de desigualdades tem duas desigualdades e duas incógnitas (x e y).
Como você provavelmente pode imaginar, resolver um sistema de desigualdades pode ser difícil em geral. Principalmente, nos concentraremos na resolução de sistemas de equações lineares, que estão intimamente relacionados com resolvendo um sistema de equações lineares

Vantagens de usar esta calculadora de desigualdade com etapas
Na verdade, resolver a maioria das desigualdades será difícil. Apenas alguns deles com estruturas muito específicas poderão ser analisados. A maioria não o fará, então é melhor você estar preparado para isso.
- Vantagem 1: Economize muito tempo: Resolver desigualdades pode levar muito tempo, pois primeiro você precisa resolver a equação associada e depois analisar os pontos críticos
- Vantagem 2: Certifique-se de dar o melhor de si para resolvê-lo: como você provavelmente já sabe, nem todas as equações ou desigualdades podem ser facilmente resolvidas, ou mesmo resolvidas. Uma calculadora com etapas tentará a melhor abordagem possível com base na estrutura detectada
- Vantagem 3: Obtenha resultados passo a passo de maneira organizada. Algumas calculadoras darão a resposta final, mas não mostrarão as etapas. Um gráfico representando as soluções também será útil
Enquanto você aprende o básico, ter uma calculadora de desigualdades que faz o trabalho pesado para você lhe mostrará como as coisas são feitas e provavelmente você adquirirá as habilidades necessárias para detectar as estruturas que são mais fáceis de enfrentar.
Existe alguma utilidade prática para as desigualdades?
Pode apostar! Na matemática básica (Álgebra e Cálculo 101), há uma ênfase mais forte em igualdades e equações. O mundo real está cheio de processos onde não temos necessariamente equações, mas temos desigualdades que vêm de limites inferiores ou superiores impostos por algumas restrições físicas.
Certos campos matemáticos avançados, como as Equações Diferenciais, baseiam os seus quadros teóricos em desigualdades (que os especialistas gostam de chamar de "estimativas de energia" em alguns contextos).
A importância das desigualdades pode não ser aparente para você, nem a necessidade de aprendê-las é muito urgente, mas, na verdade, as desigualdades constituem uma das pedras angulares da metodologia matemática usada para construir teorias, embora nos belos resultados finais tendamos a ver igualdades em vez de.

Exemplo: resolvendo desigualdades
Calcule a solução para: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Solução: Precisamos colocar todos os termos da desigualdade no lado esquerdo (poderia ser o lado direito, mas é bastante convencional usar o lado esquerdo):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]Da desigualdade acima, obtemos a equação linear associada que precisa ser resolvida primeiro:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Etapa 0: Neste caso, primeiro precisamos simplificar a equação linear dada e, para isso, realizamos as seguintes etapas de simplificação:
Resolvendo a equação linear
Colocando \(x\) no lado esquerdo e a constante no lado direito obtemos
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Agora, resolvendo para \(x\), dividindo ambos os lados da equação por \(\frac{1}{3}\), obtém-se o seguinte
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]e simplificando, finalmente obtemos o seguinte
\[\displaystyle x=-\frac{13}{4}\]Portanto, a resolução de \(x\) para determinada equação linear leva a \(x=-\frac{13}{4}\).
Análise de pontos críticos
O único ponto crítico encontrado é \(-\frac{13}{4}\).
Com base nisso, precisamos analisar os seguintes intervalos:
• Para o intervalo \(\left(-\infty, -\frac{13}{4}\right)\): O lado esquerdo é negativo, então \(\left(-\infty, -\frac{13}{4}\right)\) não faz parte da solução.
• Para o intervalo \(\left(-\frac{13}{4}, \infty\right)\): O lado esquerdo é positivo, o que significa que \(\left(-\frac{13}{4}, \infty\right)\) faz parte da solução.
Solução para a desigualdade
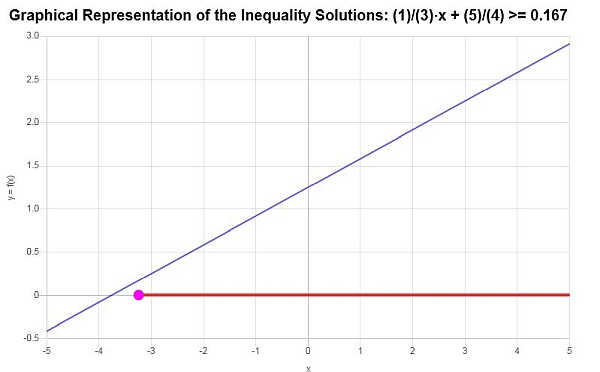
Com base na desigualdade fornecida e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(x \ge -\frac{13}{4}\).
Usando a notação de intervalo, a solução é escrita como:
\[\left[-\frac{13}{4},\infty\right)\]O gráfico de desigualdade linear da solução obtida é mostrada abaixo
Exemplo: mais exemplos de desigualdade
Encontre a solução do seguinte: \(\sin(x) > 0\)
Solução: Temos a seguinte desigualdade trigonométrica que precisa ser resolvida:
\[\sin\left(x\right) > 0\]Lidando com uma equação auxiliar
A partir da desigualdade trigonométrica acima, obtemos a equação associada que precisamos resolver primeiro:
\[\sin\left(x\right)=0\]Resolvendo a equação trigonométrica auxiliar
então as soluções são: \(x = \pi{}K\), para uma constante inteira arbitrária \(K\).
Análise de pontos críticos
Com base nas soluções da equação auxiliar, a lista de pontos críticos encontrados é: \(\pi{}K\), para uma constante inteira arbitrária \(K\).
Observe que temos um número infinito de intervalos críticos, por isso analisamos alguns deles a seguir:
• Para o intervalo \(\left(-3\pi{}, -2\pi{}\right)\): O lado esquerdo é negativo, então \(\left(-3\pi{}, -2\pi{}\right)\) não faz parte da solução.
• Para o intervalo \(\left(-2\pi{}, -\pi{}\right)\): O lado esquerdo é positivo, o que significa que \(\left(-2\pi{}, -\pi{}\right)\) faz parte da solução.
• Para o intervalo \(\left(-\pi{}, 0\right)\): O lado esquerdo é negativo, o que significa que \(\left(-\pi{}, 0\right)\) não faz parte da solução.
• Para o intervalo \(\left(0, \pi{}\right)\): O lado esquerdo é positivo, o que significa que \(\left(0, \pi{}\right)\) faz parte da solução.
• Para o intervalo \(\left(\pi{}, 2\pi{}\right)\): O lado esquerdo é negativo, então \(\left(\pi{}, 2\pi{}\right)\) não faz parte da solução.
• Para o intervalo \(\left(2\pi{}, 3\pi{}\right)\): O lado esquerdo é positivo, o que significa que \(\left(2\pi{}, 3\pi{}\right)\) faz parte da solução.
E é assim que procedemos para toda a sequência de intervalos.
Intervalos de solução de peças
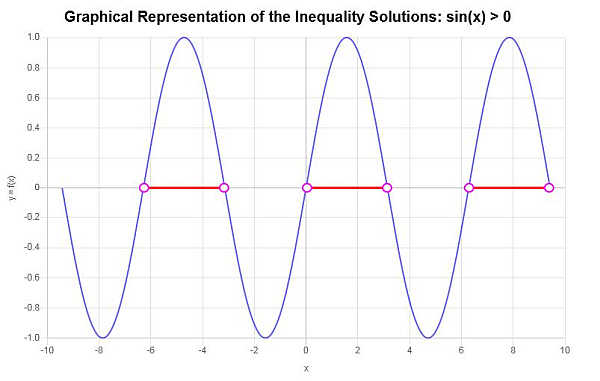
Com base na análise dos pontos críticos encontrados e dos intervalos correspondentes gerados por pontos críticos consecutivos, podemos identificar o seguinte como parte da solução da desigualdade:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]Neste caso, podemos identificar aproximadamente diferentes áreas de solução, conforme mostrado no gráfico abaixo. O gráfico de desigualdade produz a seguinte representação gráfica da solução encontrada:
Exemplo: mais desigualdades
Resolver é a desigualdade quadrática \( x^2 - 2x > 6 \).
Solução: A desigualdade que precisamos resolver é
\[x^2-2x > 6\]Colocando todos os termos da desigualdade de um lado, obtemos:
\[x^2-2x-6>0\]Equação auxiliar
Obtemos a seguinte equação auxiliar, que precisa ser resolvida primeiro:
\[x^2-2x-6=0\]Temos uma expressão polinomial no lado esquerdo, que é \(\displaystyle deg(p) = 2\), seu coeficiente inicial é \(\displaystyle a_{2} = 1\) e seu coeficiente constante é \(\displaystyle a_0 = -6\).
Fórmula quadrática
Neste caso, as raízes são calculadas usando a seguinte fórmula:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]então, descobrimos que:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]Neste caso, a equação quadrática \( \displaystyle x^2-2x-6 = 0 \), possui duas raízes reais, que se tornam pontos críticos:
Análise de pontos críticos
A lista de pontos críticos encontrados organizados em ordem crescente é: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
Com base nisso, precisamos analisar os seguintes intervalos:
• Para o intervalo \(\left(-\infty, -\sqrt{7}+1\right)\): O lado esquerdo é positivo, o que implica que \(\left(-\infty, -\sqrt{7}+1\right)\) faz parte da solução.
• Para o intervalo \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): O lado esquerdo é negativo, então \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) não faz parte da solução.
• Para o intervalo \(\left(\sqrt{7}+1, \infty\right)\): O lado esquerdo é positivo, o que significa que \(\left(\sqrt{7}+1, \infty\right)\) faz parte da solução.
Encontrando a solução para a desigualdade
Com base na desigualdade fornecida, e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(x < -\sqrt{7}+1\) ou \(x > \sqrt{7}+1\).
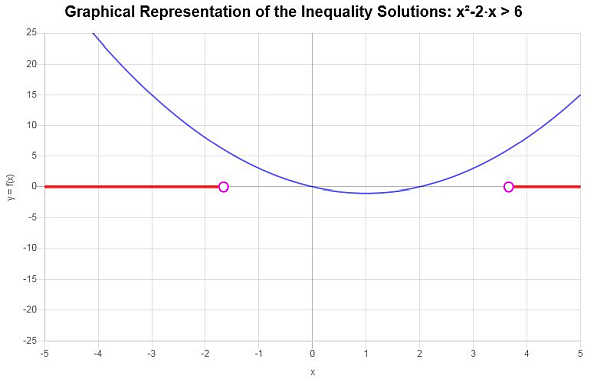
Usando a notação de intervalo, a solução é escrita como:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]A solução da desigualdade mostrada graficamente:
Mais acima das desigualdades
Você sempre começará com um calculadora de desigualdades lineares , ou talvez um calculadora de desigualdades quadráticas , porque esses são os que garantem a renderização de uma solução.
Então, mesmo com um desigualdade polinomial você pode estar enfrentando areias movediças, pois as desigualdades polinomiais também podem ser complicadas, ou mesmo impossíveis de resolver exatamente com métodos elementares.
Qualquer outro tipo de desigualdade dependerá de sua estrutura e de alguma substituição inteligente que você possa imaginar.




