A fórmula quadrática: como resolver uma equação quadrática?

A equação quadrática é uma das equações mais populares e amplamente utilizadas em matemática. Em termos de sua definição, a equação quadrática é uma equação da forma:

$$a x^2 + b x + c = 0$$

onde $a$, $b$ e $c$ são constantes, com $a \ne 0$. Esta é a maneira como um Equação quadrática é definido, onde seu termo principal $a$ deve ser diferente de zero.

A boa notícia é que a equação acima não é tão difícil de resolver, o que é ótimo considerando que a equação quadrática aparece literalmente em todos os lugares em Álgebra, Cálculo e praticamente em todos os lugares em tópicos de Matemática e Ciências.

A solução da equação quadrática

Agora, a questão é como resolver esta equação quadrática formulada acima. Felizmente, a resposta é simples e bem conhecida: A equação quadrática obtém suas soluções usando o seguinte Fórmula quadrática

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

Os valores obtidos com esta equação são conhecidos como raízes da equação quadrática (também conhecido como soluções da equação). Para analisar a natureza da solução, o discriminante é definido como:

$$D = b^2 - 4ac$$

Tipos de soluções para a fórmula quadrática

Com base no valor do discriminante, define-se a natureza das soluções. De fato, quando $D \ge 0$, então há duas soluções reais diferentes, quando $D = 0$, há uma solução real repetida, e quando $D \le 0$, há duas soluções imaginárias diferentes. Esse Solucionador de Equações Quadráticas ajuda você a fazer esses cálculos automaticamente.

Isso pode ser resumido da seguinte forma:

• Para $b^2 - 4ac > 0$: A equação tem duas raízes reais
• Para $b^2 - 4ac = 0$: A equação tem uma raiz real (repetida)
• Para $b^2 - 4ac < 0$: A equação tem duas raízes complexas

Uma das coisas legais deste solucionador de equações quadráticas é que ele mostrará as etapas para calcular a interseção y, as coordenadas do vértice e plotará a função quadrática

.

Etapas da fórmula quadrática

Existem vários passos que você deve seguir para resolver com sucesso uma equação quadrática:

Passo 1: Identifique os coeficientes. Examine a equação dada da forma $ax^2+bx+c$, e determine os coeficientes $a$, $b$ e $c$. O coeficiente $a$ é o coeficiente que aparece multiplicando o termo quadrático $x^2$.

O coeficiente $b$ é o coeficiente que aparece multiplicando o termo linear $x$, e o coeficiente $c$ é a constante.

Exemplo: Suponha que você tenha a seguinte expressão: $x^2+3x+1$. Quais são os coeficientes? Neste caso, $a = 1$ (o coeficiente que multiplica o termo quadrático $x^2$), $b = 3$ (o coeficiente que multiplica o termo linear $x$) e $c = 1$ (a constante).

Exemplo: Que tal Suponha que você tenha a seguinte expressão: $\frac{5}{4} + \frac{3}{4} x + \frac{1}{2} x^2$. Quais são os coeficientes agora? Neste caso, $a = \frac{1}{2}$ (o coeficiente que multiplica o termo quadrático $x^2$), $b = \frac{3}{4}$ (o coeficiente que multiplica o termo linear $x$) e $c = \frac{5}{4}$ (a constante).

Exemplo: O que acontece com a seguinte expressão: $-3 + \frac{1}{2} x$. Nesse caso, temos esse $a = 0$, pois a expressão não contém um termo quadrático $x^2$, portanto, nesse caso, não é uma expressão quadrática.

Passo 2: Conecte os coeficientes que você encontrou na fórmula. A fórmula é a fórmula quadrática é

$$x = \displaystyle\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

então você precisa substituir o valor dos coeficientes $a$, $b$ e $c$.

Exemplo: Se você tiver a equação: $-3x^2 + 2x-1 = 0$, encontrará $a = -3$, $b = 2$ e $c = -1$. Então, inserindo esses valores na fórmula, obtemos:

$$x = \displaystyle\frac{-2 \pm \sqrt{2^2 - 4(-3)(-1)}}{2(-3)}$$

Passo 3: Simplifique os valores na equação, depois de inserir os valores de $a$, $b$ e $c$ . No exemplo anterior, teríamos

$$x = \displaystyle\frac{-2 \pm \sqrt{4 - 12}}{-6} = \frac{-2 \pm \sqrt{-8}}{-6}$$

Passo 4: Olhe dentro da raiz quadrada. Se o valor for positivo, Equação quadrática tem duas raízes reais. Se o valor for 0, então há uma raiz real, e se o valor dentro da raiz quadrada for negativo, então há duas raízes complexas. No exemplo anterior, temos um -8 dentro da raiz quadrada, então temos duas soluções complexas, conforme mostrado abaixo:

$$x = \displaystyle\frac{-2 \pm \sqrt{4 - 12}}{-6} = \frac{-2 \pm \sqrt{-8}}{-6}= \frac{-2 \pm i \sqrt{8}}{-6}$$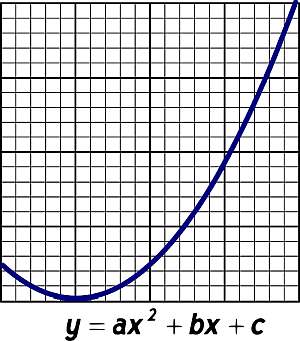

Qual é a fórmula quadrática usada para

O Fórmula quadrática é uma das fórmulas mais onipresentes na matemática. Ele aparece quando você está resolvendo todos os tipos de problemas geométricos, como quando você está maximizando uma área, dado um perímetro fixo, ou em vários problemas de palavras.

Muitas pessoas se perguntam se existe alguma relação entre esta fórmula de equação quadrática e o método de Completando o quadrado . A resposta é simples: você chega à fórmula quadrática por resolvendo a equação quadrática através do preenchimento do quadrado. É exatamente a mesma ideia, que deriva da fórmula quadrática que todos conhecemos.

Observe que as soluções da equação quadrática têm uma propriedade geométrica muito interessante: ao calcular a média das soluções encontradas, obtém-se a coordenada x do vértice da parábola, que ajuda a encontrar o forma de vértice de uma parábola, também conhecida como forma padrão, usada em muitas aplicações, exemplo de forma com seções cônicas.

Exemplos de fórmulas quadráticas

Calcule as raízes da seguinte equação quadrática: $3x^2 - 2x + 4 = 0$

Solução:

A seguinte equação precisa ser resolvida:

$$3 x^2 -2 x + 4 = 0$$

Isso corresponde a uma equação quadrática. A seguinte fórmula é usada para encontrar as soluções:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

Usando a fórmula acima, temos que:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-(-2) \pm \sqrt{ (-2)^2 - 4(3)(4)}}{2(3)}$$$$= \frac{ 2 \pm \sqrt{ -44}}{ 6}$$

Assim, as soluções são:

$$x_1 = 0.333 - 1.106 i$$ $$x_2 = 0.333 + 1.106 i$$

Portanto, existem duas soluções imaginárias $x_1 = 0.333 - 1.106 i$ e $x_2 = 0.333 + 1.106 i$.

Além disso, a interceptação y ocorre em $y = 4$, o que significa que as coordenadas da interceptação y são $(0, 4)$.

Finalmente, as coordenadas do vértice são:

$$x_V = \frac{-b}{2a} = \frac{-(-2)}{2\cdot 3} = 0.3333$$ $$y_V = f(x_V) = 3 (0.3333)^2 -2 (0.3333) + 4 = 3.6667$$