Mais sobre esta calculadora de desigualdade linear

Esta calculadora fornecerá as ferramentas necessárias para lidar com desigualdades lineares. Especificamente, você poderá resolvê-los e representá-los graficamente, seguindo todos os passos mostrados.

Desigualdades lineares como '2x + 3 < 1' ou '3x + 2y <=1' são permitidas e, dependendo do número de variáveis, você obterá um gráfico adequado junto com as etapas que levam à solução.

Uma vez fornecida uma desigualdade linear válida, tudo o que você precisa fazer é clicar em "Resolver" para iniciar o processo. Se houver algo errado ou faltando, a calculadora irá informá-lo sobre isso.

Esses tipos de desigualdade são os mais simples que você encontrará e sempre são relativamente fáceis de resolver. Este tipo junto com desigualdades quadráticas estão entre as únicas desigualdades “fáceis” de resolver.

O que é uma desigualdade linear?

Uma desigualdade linear é o tipo mais simples de desigualdade, em que todos os termos envolvidos são lineares ou constantes.

$$\displaystyle a x + b y \le 1$$

Por exemplo, a equação acima é uma equação linear com duas variáveis. Tecnicamente falando, temos desigualdade polinomial do grau 1, mas essa é uma maneira excessivamente complicada de ver as coisas.

Como você resolve uma desigualdade linear?

• Passo 1: Coloque tudo o que contém a variável que você deseja resolver de um lado e o resto do outro lado
• Passo 2: Grupo e simplificar a expressão , então para reduzir termos semelhantes
• Estágio 3: Se uma constante diferente de uma estiver multiplicando a variável que você deseja resolver, divida por ela. Uma ressalva: se você dividir por um valor negativo, será necessário mudar a direção da desigualdade

Um dos principais pontos a ter em conta, e que diferenciam os processos de resolução de equações e desigualdades, é que ao resolver equações podemos multiplicar (ou dividir) mais livremente por constantes e nada muda, enquanto que com as desigualdades precisamos de ter mais cuidado, pois multiplicar (ou dividir) por constantes negativas muda a direção da desigualdade.

Qual é a desigualdade linear mais geral

O mais geral que você pode obter com linear é

$$\displaystyle a x + bx \le c$$

mas ainda assim você pode ter '<' em vez de '$\le$'. Ou poderíamos ter

$$\displaystyle a x + bx \ge c$$

mas você também pode usar '>' em vez de '$\ge$'.

Semelhante ao que aconteceu com adição e subtração, a divisão de frações é derivada apenas da multiplicação de frações: Para dividir duas frações, basta multiplicar a primeira pela fração inversa da segunda (a fração inversa é obtida trocando o numerador pelo denominador na fração).

Formulários

As desigualdades lineares encontram muitas aplicações em matemática. Uma desigualdade linear é um tipo de média ponderada, muito adequada para todos os tipos de problemas de mistura e atribuição.

Ao lidar com problemas de palavras, geralmente você encontra equações lineares, mas não é incomum ter que lidar também com desigualdades lineares.

Uma das áreas mais conhecidas é a Otimização e Programação Linear, na qual as desigualdades lineares desempenham um papel crucial, tanto com o método Simplex como com as condições de Kuhn-Tucker quando se trata de uma função objetivo não linear.

Exemplo: resolvendo desigualdades

Resolva a seguinte desigualdade linear: $\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}$

Solução:

Precisamos colocar todos os termos da desigualdade de um lado:

$$\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0$$

Equação auxiliar associada

Precisamos resolver:

$$\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0$$

Etapa 0: Neste caso, primeiro precisamos simplificar a equação linear dada e, para isso, realizamos as seguintes etapas de simplificação:

Resolvendo a equação linear

Colocando $x$ no lado esquerdo e a constante no lado direito obtemos

$$\displaystyle \frac{2}{3}x = -\frac{17}{12}$$

Agora, resolvendo para $x$, dividindo ambos os lados da equação por $\frac{2}{3}$, obtém-se o seguinte

$$\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}$$

e simplificando, finalmente obtemos o seguinte

$$\displaystyle x=-\frac{17}{8}$$

Portanto, a resolução de $x$ para determinada equação linear leva a $x=-\frac{17}{8}$.

Pontos críticos

Como esperado para uma desigualdade linear, existe apenas um ponto crítico, que é $-\frac{17}{8}$, a partir do qual analisamos os seguintes intervalos:

• Para o intervalo $\left(-\infty, -\frac{17}{8}\right)$: O lado esquerdo é negativo, o que significa que $\left(-\infty, -\frac{17}{8}\right)$ faz parte da solução.

• Para o intervalo $\left(-\frac{17}{8}, \infty\right)$: O lado esquerdo é positivo, o que implica que $\left(-\frac{17}{8}, \infty\right)$ não faz parte da solução.

Solução para a desigualdade

Assim, verifica-se que a solução para a desigualdade é: $x < -\frac{17}{8}$.

A expressão a solução com notação de intervalo, a solução é escrita como:

$$\left(-\infty,-\frac{17}{8}\right)$$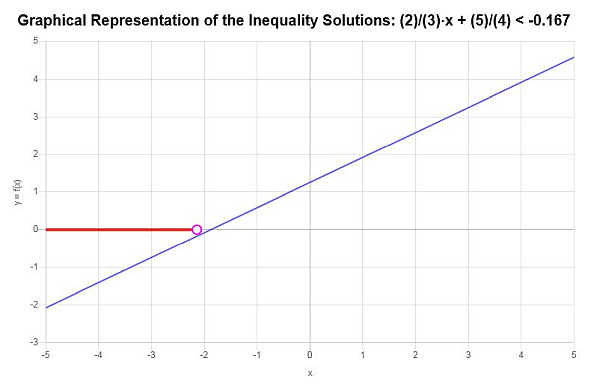

Exemplo: desigualdades mais lineares

Resolva esta desigualdade linear de 2 variáveis: $\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}$

Solução:

Precisamos resolver:

$$\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}$$

Temos uma desigualdade linear dada e precisamos resolver a variável $y$.

Neste caso, resolvemos para $y$, colocando de um lado da inequação e o resto do outro lado obtemos:

$$\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}$$

Para resolver $y$, dividimos ambos os lados da inequação por $\frac{5}{4}$ para obtermos finalmente:

$$y < -\frac{4}{15}x-\frac{2}{3}$$

Solução de desigualdade linear

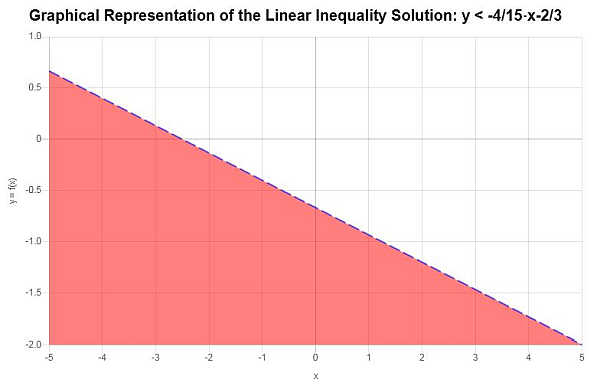
Com base na inequação fornecida, após resolvê-la para $y$ obtemos:

$$y < -\frac{4}{15}x-\frac{2}{3}$$

A representação gráfica da região de solução é mostrada no gráfico abaixo:

Mais calculadoras de álgebra

Lidar com a expressão é crucial em Álgebra. Simplificação de Expressão é o início da maioria dos processos matemáticos e geralmente é necessário reduzir as coisas à sua expressão mais simples.

Resolvendo equações e também Resolvendo Desigualdades permanecerá no centro da maioria dos processos, já que um ou outro estará no centro de quase tudo que você faz em matemática.