Calculadora diferencial
Instruções: Use esta calculadora diferencial, para encontrar o diferencial de uma função que você fornece, em um determinado ponto que você fornece, mostrando todas as etapas. Por favor, digite a função e o ponto na caixa de formulário abaixo.
Calculadora diferencial
Esta calculadora permitirá que você calcule o diferencial de uma função que você fornecer, em um ponto que você fornecer, mostrando todas as etapas do processo.
A função fornecida pode ser qualquer função diferenciável válida como f(x) = x^2 + 2x ou f(x) = x^2*sin(x), apenas para mencionar dois exemplos.
Então, quando você tiver fornecido a função e o ponto para o cálculo diferencial, basta clicar em "Calcular" para obter todas as etapas do processo mostrado.
A ideia de Diferencial é estreitamente com o da linha tangente e Aproximação Linear , pois o diferencial está medindo com precisão a variação de y, ao longo do Linha tangente no ponto dado.
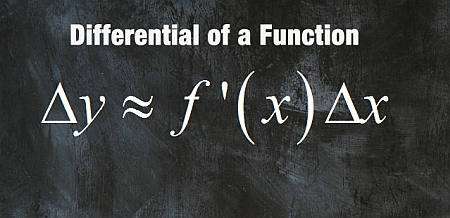
O que é um diferencial?
No cálculo diferencial, a ideia é que as derivadas fornecem informações sobre a taxa instantânea de variação de uma função em um determinado ponto.
O conceito de diferencial usa o taxa de variação determinado pela derivada em um dado ponto \(x_0\) para aproximar o comportamento da função por sua Linha tangente .
A fórmula do diferencial é baseada na ideia de que
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]onde \(\Delta y = y - f(x_0)\) e \(\Delta x = x - x_0\). Para a diferencial \(dy\), definimos
\[\displaystyle dy = f'(x_0) dx \]Essa definição (livre) é baseada na ideia de que a aproximação linear e a função se aproximam do mesmo comportamento quando \(x\) está suficientemente próximo de \(x_0\).
Etapas para calcular um diferencial
- Passo 1: Identifique a função f(x) e o ponto x0 no qual você deseja calcular a diferencial
- Passo 2: Calcule a derivada f'(x) e calcule-a em x0, para obter f'(x0). Simplifique, se necessário
- Passo 3: Use a fórmula \(\displaystyle dy = f'(x_0) dx \)
Às vezes, você encontrará o diferencial escrito como \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \), como uma forma de indicar que usará o diferencial para estimar mudanças em y, medido por \(\Delta y\).
Calculadora diferencial dy
Usando um calculadora diferencial pode economizar tempo com o processo de cálculo da derivada. A ideia do diferencial sempre foi estranha, no sentido de que parece ser vagamente definida.
Embora exista uma maneira de definir diferenciais e suas operações formalmente (um assunto chamado Formas Diferenciais), a maioria dos matemáticos não vê uma razão para a existência de diferenciais, pois eles não fornecem nenhuma informação nova que a derivada ou a aproximação de primeira ordem não forneça.
Interpretação diferencial total
A aplicação e interpretação mais comum do diferencial é quando usado em sua expressão 'finita':
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]onde você está procurando estimar a variação em y, medida por \(\Delta y\), da variação em x, medida por \(\Delta x\) e a derivada no ponto.
Às vezes, esse \(\Delta y\) é chamado de variação total ou diferencial completo .
Dicas e truques
Não se esqueça que a diferencial pode ser tomada como uma definição teórica, \(\displaystyle dy = f'(x_0) dx \), que indica a variação infinitesimal em y causada por uma variação infinitesimal em x.
Também pode ser usado em sua forma diferencial total, na qual você tem
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]que informa uma variação aproximada em y, quando para uma mudança em x (de \(x_0\) para \(x\)).
O centro de todas as calculadoras algébricas começa com o poder dos números básicos das frações.
Exemplo: calculadora diferencial
Considere a função: \(f(x) = x^2\). Encontre sua diferencial no ponto \(x_0 = 1\).
Solução: No caso deste primeiro exemplo, trabalhamos com a função \(\displaystyle f(x)=x^2\), para a qual precisamos calcular sua diferencial no ponto \(x_0 = 1\).
A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada:
Diferencial : A fórmula da diferencial para a função \(\displaystyle f(x)=x^2\) no ponto \(x_0 = 1\) é:
\[dy = f'(x_0)(x - x_0) \]Definimos \(\displaystyle y_0 = f(x_0)\), então inserir o valor do ponto \(x_0 = 1\) na função leva a:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]Além disso, inserir o valor do ponto \(x_0 = 1\) na derivada calculada leva a:
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]Então, agora inserimos esse valor na fórmula diferencial para obter:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]Conclusão : Portanto, descobrimos que a diferencial para a função \(\displaystyle f(x)=x^2\) no ponto \(x_0 = 1\) é:
\[dy = 2x-2 \]Exemplo: cálculo diferencial
Para a função dada: \(f(x) = x^3 + 3x^2 - 2\), encontre a diferencial no ponto \(x_0 = 2\).
Solução: Agora, a função para a qual precisamos encontrar a diferencial é \(\displaystyle f(x)=x^3+3x^2-2\),
Cálculo Diferencial : Usamos a seguinte fórmula para o diferencial que precisamos construir para a função dada \(\displaystyle f(x)=x^3+3x^2-2\), no ponto dado \(x_0 = \frac{1}{2}\) é:
\[dy = f'(x_0)(x - x_0) \]Observe que \(\displaystyle y_0 = f(x_0)\), o que significa que avaliando a função em \(x_0 = \frac{1}{2}\) encontramos:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]Então, obtemos a derivada no ponto \(x_0 = \frac{1}{2}\):
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]Assim, obtemos o seguinte
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]Conclusão : A conclusão final é que o diferencial que procuramos é dado por:
\[dy = \frac{15}{4}x-\frac{15}{8} \]Exemplo diferencial
Temos a função: \(f(x) = \frac{\sin(x)}{x}\). Encontre sua diferencial no ponto \(x_0 = \frac{\pi}{2}\).
Solução:
A seguinte função foi fornecida: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), para a qual precisamos calcular seu diferencial no ponto \(x_0 = \frac{\pi}{2}\).
A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada:
Cálculo : Agora é hora de encontrar o diferencial associado a \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), para o ponto dado \(x_0 = \frac{\pi}{2}\). A fórmula utilizada é:
\[dy = f'(x_0)(x - x_0) \]Colocamos o valor do ponto \(x_0 = \frac{\pi}{2}\) na derivada calculada, o que leva a:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]Portanto, usando a fórmula diferencial:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Conclusão : O diferencial correspondente é:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Outras calculadoras de diferenciação
Encontrando derivadas é sem dúvida um elemento-chave em Cálculo. Os derivativos fornecem as informações necessárias para entender o taxa de variação de funções. como aqueles têm uma conexão íntima.
Felizmente, encontrar derivadas é um processo sistemático (não necessariamente fácil) se você seguir regras de diferenciação . As regras mais usadas são as Regra Do Produto , Regra Do Quociente e Regra Da Cadeia .
Linear ou aproximações de primeira ordem tenta conceitualmente aproximar uma função por uma linha, pelo menos localmente, e pode dizer muito sobre o comportamento de uma função próximo a um determinado ponto.






