Mais sobre composição de funções

Esta calculadora permitirá que você calcular uma função composto \(f \circ g\) baseado em duas funções \(f\) e \(g\) que você fornece. Observe que, em geral, \(f \circ g\) não é o mesmo que \(g \circ f\), portanto, a ordem é relevante.

Ao calcular a composição \(f \circ g\), há uma função interna \(g\) e uma função externa \(f\), e você altera a ordem, muitas vezes o resultado varia.

Observe que \(f\) e \(g\) precisam ser funções validamente definidas, como por exemplo \(f(x) = \sqrt{x}\) e \(g(x) = 2x+1\), então teríamos que \((f \circ g)(x) = f(g(x)) = \sqrt{2x+1}\) .

O que é uma função composta?

Para formar uma função composta, você avalia uma função dentro de outra função. Sejam \(f\) e \(g\) funções, a função composta é definida como

\[\displaystyle (f \circ g)(x) = f(g(x)) \]

Quais são as etapas para encontrar a função composta?

• Etapa 1: Identifique as funções f e g para as quais você fará a composição de funções
• Passo 2: Estabeleça claramente a função interna e externa. Neste caso, assumimos que f é a função externa e g é a fórmula interna
• Passo 3: A função composta é definida como (f◦g)(x) = f(g(x))

Você pode simplificar a saída resultante de f(g(x)) e, de fato, a calculadora simplificará para você. Um ponto principal de importância é perceber que você pode precisar restringir o domínio da função composta para que fique bem definido.

O que é uma calculadora de nevoeiro

Neste caso, a névoa não é a névoa que você conhece, ela se refere à composição de f e g, escrita como \(f \circ g\).

A composição de funções estará tão algebricamente envolvida quanto a complexidade das funções que a compõem. Ou seja, a composição de funções simples levará a uma função composta simples, fácil de calcular.

Usando esta calculadora composta

A vantagem de usar esta calculadora composta é que você obterá a função composta calculada e simplificada em seus termos mais simples, mas também obterá a função composta representada graficamente.

Cadeia de função composta

A composição pode ser aplicada a mais de duas funções. Por exemplo, considere as funções \(f\), \(g\) e \(h\). A composição da cadeia é definida como

\[\displaystyle (f \circ g \circ h)(x) = f(g(h(x))) \]

onde a ordem na qual você compõe as expressões é relevante.

Domínio da calculadora de funções compostas

Observe que o domínio de uma função composta pode ser diferente das duas funções originais. Por exemplo, vejamos novamente o caso de \(f(x) = \sqrt{x}\) e \(g(x) = 2x+1\). O domínio de f é \([0, \infty)\) e o domínio de g é \((-\infty, \infty)\), mas como \((f\circ g)(x) = \sqrt{2x+1}\), o domínio de \(f\circ g\) é \([-\frac{1}{2}, \infty)\).

Exemplo: composição de funções

Calcule e represente graficamente: \((f \circ g)(x)\) para \(f(x) = \sqrt{x}\) e \(g(x) = 2x-1\).

Solução: As seguintes funções foram fornecidas: \(\displaystyle f(x)=\sqrt{x}\) e \(\displaystyle g(x)=2x-1\), para as quais precisamos calcular a função composta \(f \circ g\).

Por definição, a função composta \(f \circ g\) é definida como:

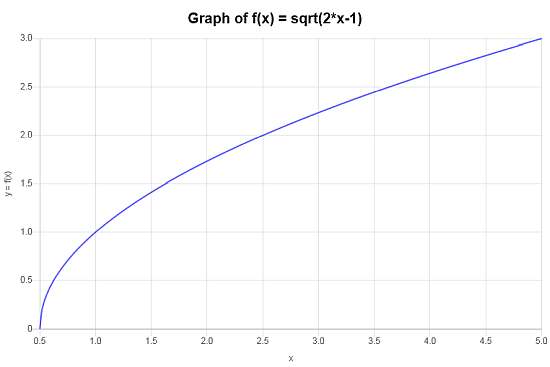
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \sqrt{2x-1} \end{array}\]

Não há nada para simplificar neste caso e, portanto, a função composta que procuramos é \(f \circ g(x)=\sqrt{2x-1}\).

O seguinte gráfico é obtido para a função composta \(f \circ g(x)=\sqrt{2x-1}\) no intervalo \([-5, 5]\):

Exemplo: cálculo de função composta

Calcule e represente graficamente: \((f \circ g)(x)\) para \(f(x) = x^{3/2}\) e \(g(x) = x+2\). \((f \circ g)(x)\) é o mesmo que \((g \circ f)(x)\) neste caso?

Solução: Estas são as funções que precisamos compor: \(\displaystyle f(x)=x^{3/2}\) e \(\displaystyle g(x)=x+2\).

Por definição, a função composta \(f \circ g\) é definida como:

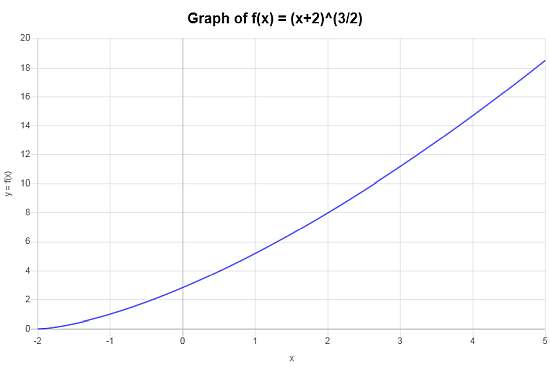
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x+2\right)^{3/2} \end{array}\]

Não há nada para simplificar neste caso e, portanto, a função composta que procuramos é \(f \circ g(x)=\left(x+2\right)^{3/2}\).

O seguinte gráfico é obtido para a função composta \(f \circ g(x)=\left(x+2\right)^{3/2}\) no intervalo \([-5, 5]\):

Exemplo: exemplo de cálculo de função composta

Encontre \((f \circ g)(x)\) para \(f(x) = x^2\) e \(g(x) = x-2\) e represente graficamente a função composta.

Solução: Neste exemplo, precisamos trabalhar com \(\displaystyle f(x)=x^2\) e \(\displaystyle g(x)=x-2\), o que exige que calculemos a função composta. \(f \circ g\).

Usando a definição, a função composta \(f \circ g\) é definida como:

\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x-2\right)^2 \end{array}\]

A expressão acima precisa ser simplificada, e as etapas são as seguintes:

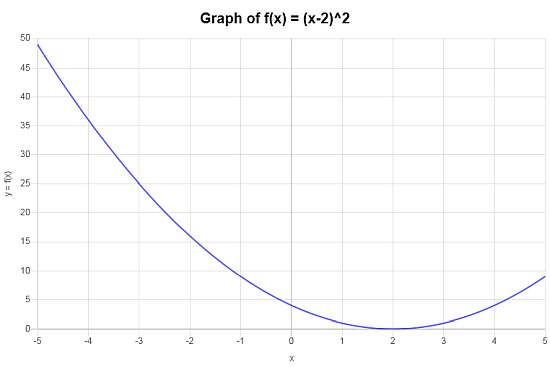
Então, depois de simplificar, a função composta obtida é \(f \circ g(x)=x^2-4x+4\).

A função composta \(f \circ g(x)=x^2-4x+4\) leva ao seguinte gráfico no intervalo \([-5, 5]\):

Mais calculadoras de álgebra

Funções são um dos principais elementos em Álgebra e Cálculo. E a razão para isso é que ele incorpora uma maneira de estabelecer uma relação entre duas variáveis x e y.

Muitos aplicativos dependem das operações que você executa e também do gráfico de uma função , que contém todas as informações 'armazenadas' na função.