Sobre a regra da cadeia

Esta calculadora permitirá que você aplique a regra da cadeia a qualquer função composta que você fornecer. A Função composta corresponde ao caso em que você avalia uma função dentro de uma função. Para que a calculadora da regra da cadeia funcione, você precisa fornecer uma função composta diferenciável válida.

Um exemplo de função válida seria f(x) = (sin(x))^2, onde aqui temos a função 'x^2' que está sendo avaliada em outra função, que é sin(x), formando um função composta.

Uma vez fornecida uma função diferenciável válida, a próxima coisa que você deve fazer é clicar no botão "Calcular", que então colocará os cálculos em movimento e você verá todas as etapas.

A derivada da regra da cadeia é uma das regras de diferenciação mais comumente usadas. Isso ocorre porque a composição da função é uma das formas mais naturais de construir novas funções com base nas elementares.

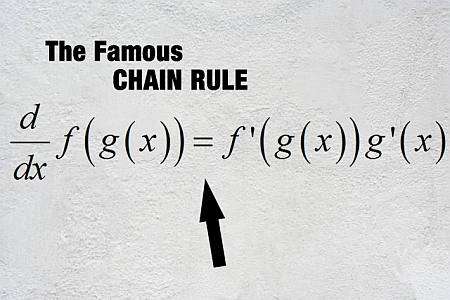
O que é a regra da cadeia

Em palavras simples, a Regra da Cadeia permite diferenciar funções compostas, ou seja, funções que são avaliadas dentro de outras funções. Então, digamos que temos as funções $f(x)$ e $g(x)$, e sabemos como calcular a derivada dessas funções, que são $f'(x)$ e $g'(x)$.

Então, há um Fórmula da Regra da Cadeia que nos permite calcular a derivada da função composta $f \circ g$, que é definida como $(f \circ g)(x) = f(g(x))$:

$$\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)$$

Passos para usar a regra da cadeia

• Passo 1: Identifique a função externa f(x) e a função interna g(x)
• Passo 2: Certifique-se de que f(x) e g(x) são funções válidas e diferenciáveis e calcule as derivadas correspondentes f'(x) e g'(x)
• Passo 3: Use a fórmula (f \circ g)'(x) = f'(g(x))g'(x), que indica que calculamos a derivada da função externa na função interna e multiplique pela derivada da função interna

Observe como as etapas acima usam a ideia de função 'interna' e 'externa'. Esse possivelmente não é um termo padrão, mas sim uma ideia que pode ajudar a identificar o papel desempenhado por cada função ao usar a Regra da Cadeia.

Aplicações da regra da cadeia

A Regra da Cadeia é de fato uma excelente ferramenta para encontrar derivadas, e normalmente será a chave de qualquer calculadora derivada , junto com todos os outros Regras de Derivadas . Mas a Regra da Cadeia tem uma interpretação especial no que é chamado Tarifas Relacionadas

Para contextualizar a ideia de taxas relacionadas, vamos começar com uma forma de escrever a Regra da Cadeia que talvez muitas pessoas achem mais fácil de entender:

$$\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx}$$

A forma acima da Regra da Cadeia está dizendo que se você $y$ é uma função de $z$ e $z$ é uma função de $x$, então, finalmente, $y$ é uma função de $x$, e você pode encontrar a derivada de $y$ em relação a $x$ usando a Regra da Cadeia.

Como você provavelmente já deve ter suspeitado, $y$ desempenha o papel de $f(x)$ (a função 'externa') e $z$ desempenha o papel de $g(x)$ (a função 'interna').

A forma acima da Regra da Cadeia vincula a taxa de variação de y em relação a x, com as taxas de variação de y em relação a z e a de z em relação a x e, portanto, o termo 'taxas relacionadas'.

Isso é extremamente útil na prática. Exemplo: o raio de um círculo está aumentando a uma taxa de 2 cm/s, qual é a taxa de variação da área do círculo? Então, você pode expressar o raio do círculo como uma função de t, refletindo o fato de que ele aumenta a uma taxa de 2 cm/s, OU você pode usar a Regra da Cadeia.

Então você chama A de área, r de raio e t de tempo. O que você precisa calcular é $\displaystyle \frac{dA}{dt}$, então você usa a regra da cadeia diretamente, já que você sabe $A = \pi r^2$, e r'(t) = 2, então

$$\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r$$

Regra da cadeia derivada parcial

Você pode usar a regra da cadeia com derivadas parciais ? Claro, a diferenciação parcial é exatamente como a diferenciação regular, só que as outras variáveis são assumidas como constantes, então o usual Regras de Derivadas aplicar.

Então, aplica-se o ideal da regra da cadeia multivariável, apenas que uma variável varia de cada vez.

Integração da regra da cadeia

A Regra da Cadeia no sentido de que não se aplica como uma ferramenta derivativa, mas se torna uma ferramenta de integração inestimável para substituições e mudanças de variáveis.

Pode ser concebido como uma espécie de regra da cadeia reversa.

Exemplo: usando a regra da cadeia

Calcule a derivada da função: $f(x) = \sin(\cos(x))$

Solução: Considere a função $\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)$. Esta função corresponde à composição de duas funções: sin(x) e cos(x), razão pela qual a Regra da Cadeia se aplicaria neste caso.

Qual é a conclusão : Podemos concluir que a derivada que procuramos é:

$$f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)$$

e isso conclui o cálculo.

Exemplo de regra da cadeia

Usando a regra da cadeia e quaisquer outras regras derivadas, calcule: $\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2$

Solução: Neste exemplo temos a função $\displaystyle f(x)=\cos\left(x^2\right)$, que corresponde a uma função composta, que indica que a Regra da Cadeia é a regra da derivada certa para começar (outras regras serão necessárias ao longo dos cálculos)

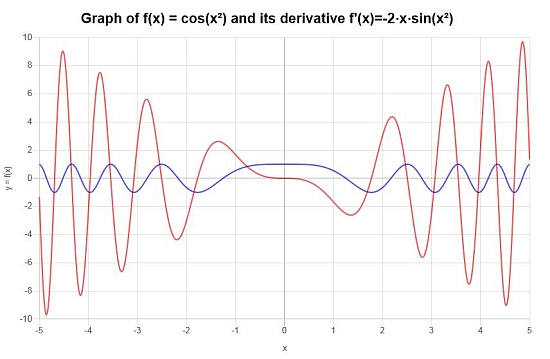
Derivada Final : A conclusão é que a derivada da função fornecida é dada por:

$$f'(x) = -2x\sin\left(x^2\right)$$>

Podemos construir a seguinte representação gráfica no intervalo $[-5, 5]$:

Exemplo: outro cálculo da regra da cadeia

Calcule a derivada de $f(x) = x^2 \sin(x^2)$ usando a regra da cadeia.

Solução:

A seguinte função foi fornecida: $\displaystyle f(x)=x^2\sin\left(x^2\right)$, para a qual precisamos calcular sua derivada.

A função já veio simplificada, então podemos proceder diretamente ao cálculo de sua derivada:

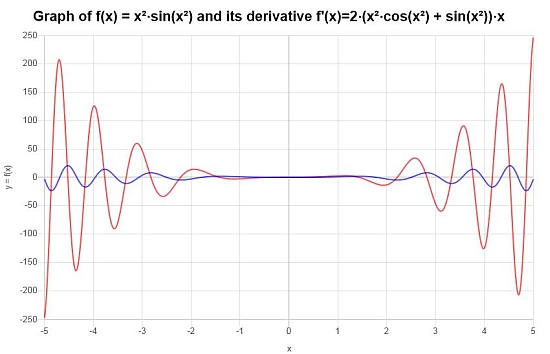
Qual é a conclusão final : A conclusão final é que a derivada que procuramos é dada por:

$$f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x$$>

Graficamente temos:

Outras calculadoras derivadas

Certamente usando um calculadora derivada facilitará as coisas ao lidar com funções bastante complicadas. O processo de diferenciação torna-se amplo, facilitado pelo uso de palavras comuns e fáceis de lembrar. Regras de Derivadas , incluindo o Regra Do Produto , o Regra Do Quociente está em Regra Da Cadeia .

Essas regras o ajudarão a lidar com todas as funções diferenciáveis, mas o processo algébrico de cálculo e simplificação pode não ser necessariamente fácil.