Mais sobre esta calculadora de vértices

Esta calculadora permitirá que você obtenha uma função quadrática que você fornece em Vertex Form , mostrando todas as etapas. Você precisa fornecer uma expressão quadrática válida em x. Qualquer função quadrática válida funcionará.

Por exemplo, você pode fornecer algo como x^2 + 3x + 4 ou talvez uma expressão que não seja simplificada, como x^2 + 3x - 1/2 x + 3x^2 - 3.

Depois de fornecer uma função quadrática válida, basta clicar em "Calcular" e o cálculo da forma do vértice será mostrado para você, com todas as etapas fornecidas por este calculadora de parábola .

Toda função quadrática validamente definida terá uma forma de vértice, a partir da qual será direto obter as coordenadas do vértice e se a parábola abre "para cima" ou "para baixo".

Como encontrar a forma do vértice de uma parábola?

Todas as funções quadráticas são representadas graficamente por uma parábola. Esta parábola será aberta para cima ou para baixo, dependendo do sinal do coeficiente líder.

Em última análise, obter a parábola em forma de vértice consiste em encontrar o vértice da função quadrática, o que é obtido por Completando o quadrado .

Quais são as etapas para calcular a forma do vértice?

Então, como você encontra a forma de vértice ? Você pode seguir estas etapas:

• Passo 1: Identifique a função quadrática. A expressão tem que ter grau 2, e o coeficiente líder que multiplica x² precisa ser diferente de zero
• Passo 2: Se o coeficiente líder que multiplica x² for positivo, a parábola abre para cima e, se for negativo, abre para baixo
• Passo 3: Complete os quadrados, e observe o termo dentro dos parênteses com x, pois ele determina a coordenada x do vértice
• Passo 4: Depois de completar os quadrados, a constante fora do parêntese (pode ser zero) corresponde à coordenada y do vértice

Portanto, podemos ver que o processo geral de cálculo da forma do vértice está intimamente relacionado com o processo de completar os quadrados.

Existe uma fórmula de vértice?

De fato, sim, existe. Normalmente, o processo de conclusão dos quadrados é o longo caminho a percorrer. Suponha que você tenha um função quadrática , Expresso por:

\[ f(x) = a x^2 + b x + c\]

Então, você já tem uma função quadrática simplificada. A coordenada x do vértice é calculada usando a seguinte fórmula:

\[ x_v = \displaystyle \frac{-b}{2a} \]

Realmente simples, certo? Sim. Mas então, como você obtém a coordenada y do vértice? Você pega o valor \(x_v\) e o insere na função quadrática. Então nós pegamos

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

Naturalmente, essa fórmula pode ser muito mais rápida do que fazer um processo de completar quadrados, mas cada método tem sua utilidade, e as circunstâncias de um determinado problema dirão qual forma usar. .

Forma quadrática para vértice?

Por que você iria querer ir da forma quadrática para a forma de vértice? Há muitas razões: de um ponto de vista geométrico, a forma do vértice permite ver a função quadrática dada como uma translação e redimensionamento de uma parábola elementar, onde a translação é determinada pelo vértice e a escala é determinada com o líder coeficiente.

O cálculo pode ser trabalhoso, mas isso calculadora de parábola fará o trabalho pesado para você.

Padrão para forma de vértice?

Geralmente há um pouco de confusão sobre isso. Deixe-me esclarecer, a forma de vértice é outro nome dado à forma padrão. Então, a forma padrão de uma função quadrática \(y = a(x-h)^2 + k\) é a mesma que a forma do vértice.

A confusão surge porque às vezes as pessoas usam a forma geral de uma quadrática quando se referem à forma padrão. A forma geral é \(y = ax^2 + bx + c\).

Então, a questão que faz sentido é como passar da forma geral para a forma vértice, que é o mesmo que perguntar como ir da forma geral para a forma padrão. A resposta é simples: Comece da forma geral e então você Complete os quadrados para chegar ao formulário padrão.

Exemplo: como encontrar a forma do vértice

Encontre o vértice da seguinte expressão quadrática \(f(x) = x^2 + 3x - 6\) usando a fórmula do vértice

Solução: Precisamos encontrar a forma do vértice para a função quadrática \(\displaystyle f(x)=x^2+3x-6\).

Primeiro calculamos as coordenadas do vértice para a parábola associada à função quadrática dada.

Para uma função quadrática na forma \(f(x) = a x^2 + bx + c\), a coordenada x do vértice é calculada usando a seguinte fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Nesse caso, temos que a função para a qual precisamos encontrar o vértice é \(f(x) = \displaystyle x^2+3x-6\), o que implica que os coeficientes correspondentes são:

\[a = 1\] \[b = 3\] \[c = -6\]

Colocando os valores conhecidos de \(a\) e \(b\) na fórmula da coordenada x do vértice, obtemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

Agora, precisamos inserir o valor de \(x_V = \displaystyle -\frac{3}{2}\) na função quadrática, então obtemos:

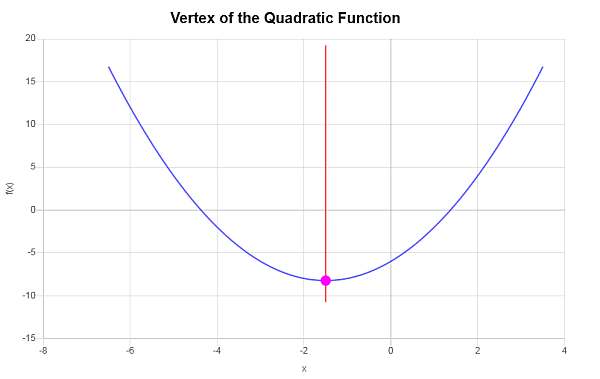
\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

Portanto, a coordenada x do vértice é \(x_V = \displaystyle -\frac{3}{2}\) e a coordenada y do vértice é \(y_V = \displaystyle -\frac{33}{4}\). Isso indica que o ponto que representa o vértice é \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\).

O seguinte é obtido graficamente:

Precisamos completar o quadrado para a expressão quadrática \(\displaystyle x^2+6x-2\).

Os seguintes passos devem ser seguidos para completar o quadrado:

Passo 1: Neste caso, como a constante principal, o termo que multiplica \(x^2\) no polinômio dado, é \(a = 1\), então não devemos fatorá-lo.

Passo 2: Forçamos um '2' na frente do termo \(x\) observando que o termo de ordem 1 na expressão quadrática dada pode ser reescrito: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), então obtemos \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Estágio 3: O termo que multiplica 2 neste caso é \(\displaystyle 3\), então para usar a equação binomial, precisamos que seu quadrado \(\displaystyle \left(3\right)^2\) esteja na expressão.

Para isso, somamos e subtraímos agora o termo \(\displaystyle \left(3\right)^2 = 9\), para completar o quadrado. Somar e subtrair o mesmo termo é o mesmo que somar zero, portanto não afeta a expressão: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Passo 4: Completamos o quadrado e simplificamos as constantes: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusão: Portanto, descobrimos que a função na forma de vértice é \(\displaystyle f(x) = \left( x+3 \right)^2-11\), que completa o cálculo.

Exemplo: forma quadrática para vértice

Converta a seguinte forma quadrática \(f(x) = x^2 + 6x - 2\) na forma de vértice. Quais são as coordenadas do vértice? A parábola tem concavidade para cima ou para baixo?

Solução:

Precisamos encontrar a forma do vértice para a função quadrática \(\displaystyle f(x)=x^2+6x-2\).

Primeiro calculamos as coordenadas do vértice para a parábola associada à função quadrática dada.

Para uma função quadrática na forma \(f(x) = a x^2 + bx + c\), a coordenada x do vértice é calculada usando a seguinte fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Nesse caso, temos que a função para a qual precisamos encontrar o vértice é \(f(x) = \displaystyle x^2+6x-2\), o que implica que os coeficientes correspondentes são:

\[a = 1\] \[b = 6\] \[c = -2\]

Colocando os valores conhecidos de \(a\) e \(b\) na fórmula da coordenada x do vértice, obtemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{6}{2 \cdot 1} = -3\]

Agora, precisamos inserir o valor de \(x_V = \displaystyle -3\) na função quadrática, então obtemos:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

Portanto, a coordenada x do vértice é \(x_V = \displaystyle -3\) e a coordenada y do vértice é \(y_V = \displaystyle -11\). Isso indica que o ponto que representa o vértice é \( \displaystyle \left(-3, -11\right)\).

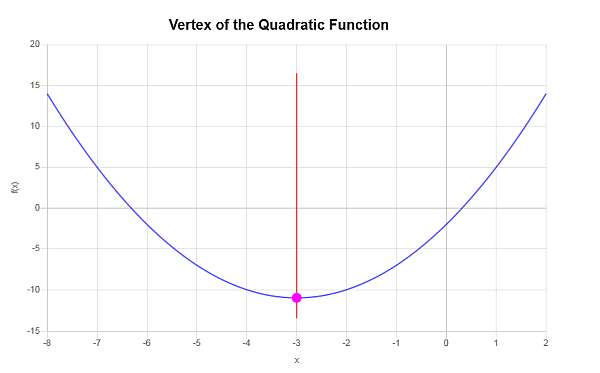
Precisamos completar o quadrado para a expressão quadrática \(\displaystyle x^2+6x-2\).

Os seguintes passos devem ser seguidos para completar o quadrado:

Passo 1: Neste caso, como a constante principal, o termo que multiplica \(x^2\) no polinômio dado, é \(a = 1\), então não devemos fatorá-lo.

Passo 2: Forçamos um '2' na frente do termo \(x\) observando que o termo de ordem 1 na expressão quadrática dada pode ser reescrito: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), então obtemos \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Estágio 3: O termo que multiplica 2 neste caso é \(\displaystyle 3\), então para usar a equação binomial, precisamos que seu quadrado \(\displaystyle \left(3\right)^2\) esteja na expressão.

Para isso, somamos e subtraímos agora o termo \(\displaystyle \left(3\right)^2 = 9\), para completar o quadrado. Somar e subtrair o mesmo termo é o mesmo que somar zero, portanto não afeta a expressão: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Passo 4: Completamos o quadrado e simplificamos as constantes: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusão: Portanto, descobrimos que a função na forma de vértice é \(\displaystyle f(x) = \left( x+3 \right)^2-11\), que completa o cálculo.

Outras calculadoras quadráticas

O máximo de calculadoras quadráticas confiar de uma forma ou de outra no processo de completando os quadrados , que permite agrupar coisas dentro de parênteses que estão ao quadrado.

Como podemos ver na fórmula do vértice, o cálculo do vértice está intimamente ligado ao Fórmula quadrática está em raízes de cálculo da equação quadrática . .