Funzioni razionali

Questa calcolatrice di funzioni razionali vi permetterà di analizzare i punti più rilevanti di una funzione razionale da voi fornita, con tutti i passaggi indicati. In genere, per la maggior parte delle funzioni razionali è possibile trovare le intercette, gli asintoti verticali e il grafico. Alcune funzioni razionali specifiche presentano anche asintoti orizzontali.

Il tipo di funzione che si può fornire è del tipo 'f(x)=1/x - x', o qualcosa che coinvolge polinomi di grado superiore come 'f(x) = (x^3-1)/(x^2+x)'

Una volta fornita una funzione razionale valida, è possibile fare clic sul pulsante Calcola e verranno mostrati tutti i passaggi.

Uno degli attributi principali di una funzione razionale è che è possibile ridurre il calcolo al problema di risoluzione di equazioni polinomiali , che è uno dei tipi più "semplici" di equazioni che si possono risolvere .

Cos'è una funzione razionale

Una funzione razionale è una funzione che coinvolge la quoziente di due polinomi \(P(x)\) e \(Q(x)\), dove il divisore \(Q(x)\) non è uguale al polinomio zero. La formula della funzione razionale è quindi

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

Ad esempio, la funzione

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

è una funzione razionale, perché è proprio il quoziente di due polinomi. Ma per esempio

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

non è razionale perché il divisore non è un polinomio. Osservate che quando diciamo che il divisore \(Q(x)\) non è uguale al polinomio zero, NON stiamo dicendo che \(Q(x)\) non può avere zeri. Ad esempio, nel caso di \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \), il divisore è \(Q(x) = x + 1\), che ha uno zero in corrispondenza di \(x = -1\).

Quello che non vogliamo è qualcosa come

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

perché, sebbene in questo caso \(Q(x) = 0\) sia tecnicamente un polinomio, è il polinomio zero (che è zero ovunque).

Passi per il calcolo di una funzione razionale

• Passo 1: Innanzitutto, assicuratevi di avere una funzione razionale, di cui potete identificare il numeratore P(x) e il denominatore Q(x)
• Passo 2: Se non si trova la struttura descritta sopra, ci si ferma. Potrebbe essere necessario raggruppare i termini tramite riduzioni algebriche .
• Passaggio 3: È necessario trovare gli eventuali zeri reali di P(x) e Q(x). Le conclusioni trovate saranno strettamente legate agli zeri di P(x) e Q(x)
• Passaggio 4: Per trovare l'intercetta y, si valuta la funzione a zero, calcolando f(0). L'intercetta y sarà ben definita se x = 0 non è uno zero di Q(x)
• Passaggio 5: Per trovare le intercette delle x, si ottengono gli zeri di P(x) che non sono zeri di Q(x)
• Passaggio 6: Per trovare gli asintoti verticali, è necessario trovare gli zeri di Q(x) che non siano zeri di P(x)
• Passaggio 7: Per trovare gli asintoti orizzontali, è necessario che il grado di Q(x) sia maggiore o uguale al grado di P(x)

Si osservi che, come ci si aspetta, l'analisi di una funzione razionale dipende da Trovare gli zeri di un polinomio e poi mettere insieme tutte le conclusioni. .

Si noti che il dominio di una funzione razionale è l'intera linea reale, ad eccezione degli zeri del divisore Q(x). Se esiste uno zero di Q(x) che è anche uno zero di P(x), allora la discontinuità può essere riparata. L'intervallo di una funzione razionale dipende dai gradi di P(x) e Q(x).

Perché usare le funzioni razionali

Le funzioni razionali vengono utilizzate perché sono estensioni naturali dei polinomi. Si possono considerare come il passo successivo nella complessità di una funzione. Come sappiamo, espressioni polinomiali sono tra le funzioni più semplici che si possano trovare, eppure sono anche tra le più utili.

Le equazioni razionali compaiono in genere nei problemi di mescolanza più avanzati, eppure sono sorprendentemente semplici da gestire, a patto che i polinomi coinvolti siano abbastanza semplici. Sappiamo che come risolvere le equazioni quadratiche ma per i polinomi di grado 3 e superiore le cose possono essere più complicate.

Le funzioni polinomiali sono anche funzioni razionali?

Sì, se P(x) è un polinomio, allora P(x) è anche razionale, perché possiamo scrivere:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

e Q(x) = 1 è un polinomio vero e proprio. Non è vero il contrario: una funzione razionale non è necessariamente un polinomio. Perché? Perché naturalmente, a meno che Q(x) = 1, ogni volta che si ha \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), non si avrà che tutti i termini siano termini liberi, come richiesto dalla definizione di polinomio.

Più formalmente, utilizzando Teorema Del Resto , abbiamo

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

dove \(d(x)\) è un polinomio, ma \frac{r(x)}{Q(x)} non lo è, perché il grado di r(x) è inferiore al grado di Q(x).

Esempio: lavorare con le funzioni razionali

Trovare le intercette e gli asintoti e il grafico di : \(f(x) = \frac{x^2-1}{x+1}\)

Soluzione:

Ci è stata fornita la seguente funzione:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

È necessario trovare le intercette e gli asintoti, se presenti. Successivamente, verrà presentato il grafico della funzione.

Troviamo gli zeri della funzione data. Dobbiamo risolvere la seguente equazione razionale:

\[\frac{x^2-1}{x+1}=0\]

Osserviamo che per \(x \ne -1\) possiamo semplificare come:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Equazione ausiliaria del numeratore

Ora poniamo il numeratore uguale a zero e troviamo le soluzioni. Le radici che non rendono il denominatore uguale a zero saranno soluzioni dell'equazione razionale.

Per trovare le radici del numeratore è necessario risolvere il seguente problema: \(x^2-1=0\)

Per un'equazione quadratica della forma \(a x^2 + bx + c = 0\), le radici vengono calcolate utilizzando la seguente formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In questo caso, abbiamo che l'equazione da risolvere è \(\displaystyle x^2-1 = 0\), il che implica che i coefficienti corrispondenti sono:

\[a = 1\] \[b = 0\] \[c = -1\]

Innanzitutto, calcoleremo il discriminante per valutare la natura delle radici. La discriminante è calcolata come:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Poiché in questo caso otteniamo che il discriminante è \(\Delta = \displaystyle 4 > 0\), che è positivo, sappiamo che l'equazione ha due radici reali diverse.

Ora, inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

allora, troviamo che:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Equazione ausiliaria del denominatore

Dobbiamo trovare le radici del denominatore: \(x+1=0\)

Pertanto, la soluzione di \(x\) per l'equazione lineare data porta a \(x=-1\).

Zeri al numeratore e al denominatore

In base all'analisi mostrata sopra, gli zeri reali del numeratore della funzione razionale data sono \( x_{ 1} = -1\) e \( x_{ 2} = 1\).

Si scopre inoltre che il denominatore ha uno zero reale, che è \( x_{ 1} = -1\).

Trovare le intercette x

In base agli zeri del numeratore che non sono zeri del denominatore, troviamo che esiste un'intercetta x, che è \(\left(1, 0\right)\).

Trovare le intercette y

Valutando la funzione fornita a \(x = 0\), si scopre che:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

quindi l'intercetta y è \( \left(0, -1\right)\).

Asintoti verticali

Dopo aver analizzato gli zeri, si conclude che la funzione non ha asintoti verticali.

Asintoti orizzontali

Si noti che il grado del numeratore è \(2\) e il grado del denominatore è \(1\) e quindi, poiché il grado del polinomio al numeratore supera quello del polinomio al denominatore, si conclude che non esiste un asintoto orizzontale.

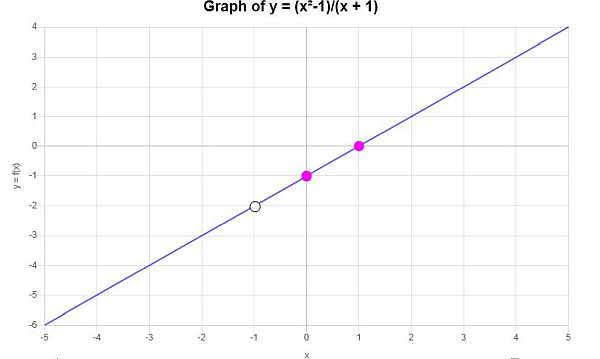
Si ottiene il seguente grafico:

Esempio: asintoti orizzontali

Questa funzione razionale ha un asintoto orizzontale: \(f(x) = \frac{x^2-1}{x^2+1}\)?

Soluzione: È evidente che in questo caso la funzione è costituita dal quoziente di due polinomi, entrambi di grado pari a 2. Hanno cioè lo stesso grado e quindi esiste un asintoto orizzontale.

Lo si può vedere anche utilizzando i limiti:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

il che implica che l'asintoto orizzontale è \(y = 1\). Questo conclude il calcolo.

Calcolatori di funzioni utili

Le funzioni sono oggetti matematici fondamentali, che racchiudono la relazione tra diverse variabili. Utilizzando una Calcolatrice di funzioni può aiutare a gestire sistematicamente le funzioni che potrebbero essere troppo complicate da gestire a mano.

Grafici di funzioni razionali è uno degli esempi di gioco più comuni che gli studenti imparano in Algebra e in Calcolo, e anche se forse le funzioni razionali non compaiono di per sé molto spesso nelle applicazioni, le capacità analitiche necessarie per affrontarle possono rivelarsi preziose

Lo stesso vale per Risolvere equazioni razionali in questo caso, i principi della manipolazione delle espressioni algebriche e della loro riduzione ai termini inferiori si riveleranno estremamente efficaci per il raggiungimento di competenze più avanzate.

Ora, se parliamo di funzioni, non possiamo dimenticare la calcolo della derivata di una funzione , integrazione e altre tecniche infinitesimali più avanzate.