Risolvere equazioni razionali

Utilizzando questa calcolatrice con passaggi sarete in grado di lavorare facilmente con la risoluzione di equazioni razionali. Il modo in cui funziona è che dovete semplicemente fornire un'equazione razionale nel riquadro in alto. Questa equazione può essere semplice come 'x^(1/2) = x^(1/4)', o più complicata se necessario.

Una volta terminata la digitazione o l'incollaggio dell'equazione desiderata, è possibile fare clic sul pulsante "Risolvi" risolvere l'equazione e mostrerà tutti i passaggi del percorso.

Le equazioni razionali, come altri tipi di equazioni non lineari, sono in generale difficili da risolvere, ammesso che si riesca a risolverle. Di solito, solo alcune Equazioni razionali con alcune strutture specifiche possono essere risolte in modo esplicito utilizzando alcuni trucchi standard, come l'uso di sostituzioni.

Cos'è un'equazione razionale

Un'equazione razionale è un tipo di equazione che si trova in algebra, in cui in qualche punto dell'equazione si vede un quoziente di due polinomi. Per esempio

\[\displaystyle \frac{x}{x+1} + 4 = 1\]

è un'equazione razionale, a causa del termine \(\frac{x}{x+1} \). Tecnicamente, tutte le equazioni polinomiali sono anche equazioni razionali, perché un polinomio si può sempre considerare diviso per 1 e 1 è un polinomio di ordine 0 (una costante).

Quello sopra è un modo elegante di esprimere questa \(P(x) = \frac{P(x)}{1}\).

Formula dell'equazione razionale

Non esiste una formula specifica per un'equazione razionale, ma dovreste essere in grado di identificarla ogni volta che il quoziente di due denominatori compare in un'equazione. In termini di formula, si cerca di identificare qualcosa come:

\[\displaystyle \frac{P(x)}{Q(x)} \]

da qualche parte nell'equazione, per poterla classificare come equazione razionale.

Come risolvere le equazioni razionali

Ad esempio, se si deve risolvere l'equazione razionale \(\frac{1}{x} + \frac{1}{x^2} = 2\), si potrebbe ricorrere al metodo più lungo di trovare il denominatore comune, che in questo caso sarebbe \(x^2\) e si arriverebbe a un'equazione polinomiale.

Ma poi si potrebbe anche fare la sostituzione \(u = \frac{1}{x}\), in modo che l'equazione si trasformi nell'equazione ausiliaria \(u + u^2 = 2\), che può essere immediatamente risolta con la formula Formula dell'equazione quadratica .

Relazione con le espressioni razionali

Espressioni razionali e il semplificazione di un'espressione razionale è un compito cruciale al momento di risolvere equazioni che coinvolgono espressioni razionali.

Allo stesso tempo, però, prima di lanciarsi alla cieca nella semplificazione e nel funzionamento dell'equazione in questione, è bene valutare se esiste una sostituzione che riduca il tutto a un'equazione ausiliaria molto semplice.

Come utilizzare la calcolatrice di equazioni razionali con i passi necessari

Il vantaggio della nostra calcolatrice è che eseguirà il calcolo mostrandovi i passaggi, il che può sicuramente essere utile. L'aspetto principale è che non tutte le equazioni razionali hanno una soluzione che possiamo trovare con i metodi elementari.

Risolvere le equazioni a volte ci vuole un po' di astuzia, ma con la nostra calcolatrice eliminerete le congetture.

Esempio: una semplice equazione razionale

Risolvere la seguente equazione: \(\frac{1}{x} + \frac{1}{x^2} = 2\)

Soluzione: Si ottiene la seguente equazione

\[\frac{1}{x}+\frac{1}{x^2}=2\]

Utilizziamo la sostituzione: \(u = \frac{1}{x}\) per cui l'equazione diventa:

\[u + u^2 = 2\]

L'equazione quadratica può essere espressa con la formula \(u^2 + u - 2 = (u-1)(u+2) = 0\)

che porta direttamente alla soluzione \(u = 1, u = -2\). Ma poiché sappiamo che \(u = \frac{1}{x}\), troviamo la seguente soluzione all'equazione originale:

\[x_1 = -\frac{1}{2} \] \[x_2 = 1 \]

Pertanto, la soluzione di \(x\) per l'equazione data porta alla soluzione \(x=-\frac{1}{2},\,\,x=1\).

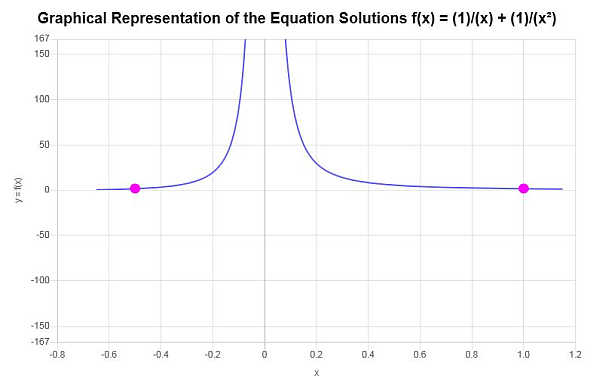
Graficamente

Di seguito è riportata la rappresentazione grafica delle soluzioni ottenute:

Altre calcolatrici di equazioni

La Maggior Parte Calcolatori di equazioni sfrutteranno strutture specifiche per cercare di trovare una soluzione esatta, ma non sempre gli sforzi avranno successo.

Ma in definitiva non si può fare molto in generale. L'unica cosa che possiamo fare è Risolvi equazioni lineari E risolvere equazioni polinomiali (in una certa misura, solo equazioni quadratiche sono davvero semplici da risolvere).

Quindi, qualsiasi strategia per la risoluzione di un'equazione ha a che fare con una qualche trasformazione della stessa, utilizzando un qualche riduzione algebrica nei pochi tipi di equazioni che sappiamo effettivamente come risolvere. Per lo più, tutto ciò che possiamo fare è tentare qualche sostituzione fortunata, se si è abbastanza fortunati.