Calcolatore derivato

Questo calcolatore di derivate ti guiderà attraverso tutti i passaggi e le regole utilizzate per trovare la derivata di una data funzione. Devi digitare una funzione come 3x + sin(x^2), oppure puoi farla precedere dall'intera definizione della funzione, come f(x) = 3x^ 2 + 2tan(x^3).

Si noti che questo può essere indicato come un calcolatore della prima derivata uguale a un calcolatore della derivata. Derivata prima e derivata rappresentano la stessa cosa e la parte "prima" di solito viene eliminata.

La funzione fornita può essere completamente semplificata o meno, non importa, poiché la calcolatrice semplificherà prima la funzione, se necessario, prima di calcolarne la derivata.

Una volta a funzione valida è stato fornito, devi solo cliccare su "Calcola", attendere qualche secondo e ti verranno presentati tutti i passaggi del calcolo.

La differenziazione è lo strumento principale utilizzato nel calcolo (insieme all'integrazione) ed è un'operazione cruciale ampiamente utilizzata nella matematica più avanzata. Alcune applicazioni molto comuni includono calcolo della tangente , massimi e minimi e molto altro ancora.

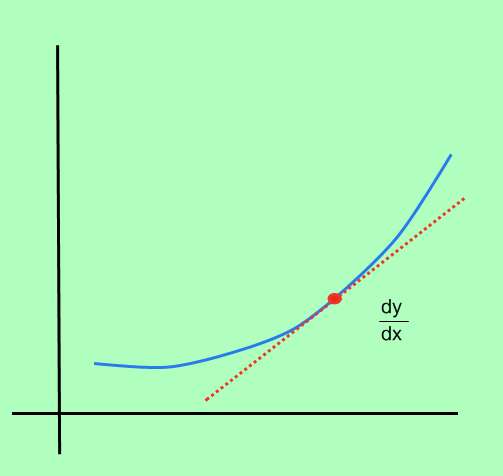
Come calcolare la derivata di una funzione?

Viene chiamato il processo di calcolo della derivata di una funzione differenziazione , e consiste nel determinare la velocità di variazione istantanea del punto, in ogni punto nel dominio della funzione.

Qual è la velocità di variazione istantanea di una funzione? Bene, iniziamo con la definizione di tasso di cambio : Si consideri una funzione \(f\) e si assuma di avere due punti, \(x_0\) e \(x_1\). Nel punto \(x_0\) la funzione è \(f(x_0)\) e nel punto \(x_1\) la funzione assume il valore \(f(x_1)\)

Quindi, la variazione di f è definita come \(\Delta y = f(x_1) - f(x_0)\) (a cui ci si riferisce anche come variazione di y). Inoltre, la variazione di x è definita come \(\Delta x = x_1 - x_0)\). In parole semplici, \(\Delta x\) è la variazione di x, mentre \(\Delta y\) è la variazione del valore della funzione, dovuta alla variazione di x.

Graficamente:

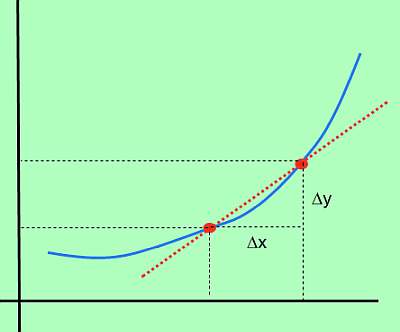
Formula derivata

Quindi, se \(\Delta x\) rappresenta la variazione di x, e\(\Delta y\) rappresenta la variazione del valore della funzione, dovuta alla variazione di x, il corrispondente tasso di cambio È:

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

Allora, quale sarebbe il tasso di cambiamento istantaneo? Ciò corrisponderebbe all'analisi di cosa accadrebbe se \(\Delta x\) diventasse davvero piccolo. Ci si aspetterebbe che anche \(\Delta y\) diventi piccolo, ma ciò accadrebbe al tasso tra \(\Delta y\) e \(\Delta x\)?

Quindi, in questo contesto, il tasso di cambiamento istantaneo è definito come

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

Quindi, in parole povere, impostiamo \(x_0\) fisso e calcoliamo il tasso di variazione per i valori di \(x_1\) che sono sempre più vicini a \(x_0\). Usando questa idea di tasso di variazione istantaneo, possiamo dare la seguente formula per la derivata in un punto \(x_0\).

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

Se il limite sopra vale, diciamo che la funzione f è differenziabile in \(x_0\). Inoltre, diremo che una funzione è differenziabile in un insieme A, se la funzione è differenziabile in ogni punto dell'insieme.

Passaggi per l'utilizzo della formula derivata

• Passo 1: Identifica chiaramente la funzione f che vuoi differenziare
• Passo 2: Assicurati di semplificare f il più possibile, altrimenti trovare il limite richiesto potrebbe essere inutilmente più difficile
• Passaggio 3: Decidi se lavorerai con un punto generico x0 o se fornirai un punto numerico specifico per x0
• Passaggio 4: In base alla definizione della funzione, utilizzare la formula \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). Cioè, collega i valori di x0 e x1 in f, e guarda come appare la formula algebricamente
• Passaggio 5: Semplifica il più possibile PRIMA di prendere il limite
• Passaggio 6: A volte è più facile impostare x1 = x0 + h, e quindi calcolare il limite quando h converge a 0

Si noti che il passaggio 6 è quello che ad alcune persone piace come predefinito. Infatti, la formula derivata alternativa che può sembrare più semplice ai fini della semplificazione è:

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

che è la formula che potresti trovare nel tuo libro di testo, invece dell'altra.

Regole derivate

Sembrerebbe un sacco di lavoro calcolare la derivata usando la formula. E in effetti, potrebbe essere un processo laborioso se decidessimo di elaborare ogni processo di differenziazione utilizzando la formula derivata.

Fortunatamente, ci sono una serie di funzioni (vale a dire polinomio , funzioni trigonometriche ) di cui sappiamo con precisione quali sono le loro derivate.

Inoltre, abbiamo regole di differenziazione che ci permettono di trovare la derivata di una funzione che è a Funzione composta e/o una combinazione di funzioni elementari (di cui conosciamo la derivata), in termini di derivate elementari.

Quali sono i passaggi per il calcolo della derivata?

• Passo 1: Identifica la funzione f che vuoi differenziare. Semplifica il più possibile PRIMA di calcolarne la derivata
• Passo 2: Determina se sei obbligato o meno a utilizzare la formula derivata o meno
• Passaggio 3: Se devi usare la formula derivata, usa \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), oppure puoi usare \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \) se ti sembra più facile avvicinarti
• Passaggio 4: Se non è necessario utilizzare la formula della derivata, è possibile utilizzare le principali regole di differenziazione: linearità, Regola Del Prodotto , Regola Del Quoziente E Regola Di Derivazione , che ti aiuterà a ridurre il calcolo della derivata all'utilizzo di derivate note di base

Spesso, la funzione che stai cercando di eseguire trova la derivata for non è una funzione semplice, ma è una combinazione di base di diverse funzioni semplici. Ad esempio, la funzione

\[f(x) = x + \cos(x) + \sin(x)\]

non è una funzione elementare in sé, ma lo è Funzione composta di tre funzioni elementari, \(x\), \(\sin x\) e \(\cos x\).

Applicazioni dei derivati

Si potrebbe pensare "beh, le derivate implicano dei limiti e questo è super teorico, quindi non deve avere troppe applicazioni", ma ti sbaglieresti completamente. La magia delle derivate è che riguardano essenzialmente il tasso di variazione delle funzioni, che possono rappresentare diversi tipi di processi.

Ecco perché la differenziazione consente di studiare il processo di cambiamento e come confrontare le variabili mutevoli, che ha un'ampia applicabilità.

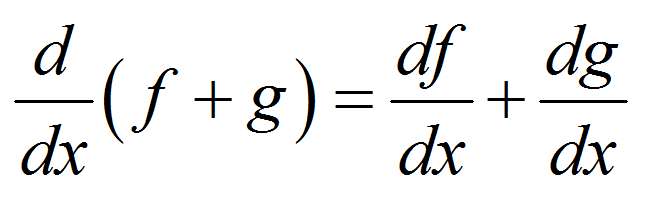
Esempio: calcolo della derivata

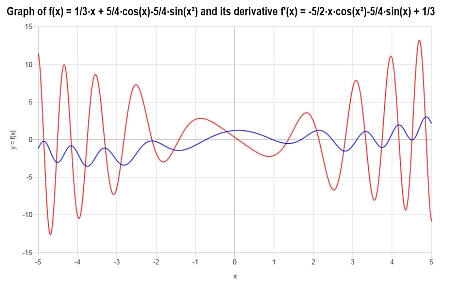
Calcola la derivata rispetto a x per \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)

Soluzione: E' stata fornita la seguente funzione: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), per la quale dobbiamo calcolare la sua derivata.

Passaggio Iniziale: In questo caso, dobbiamo prima semplificare la data funzione \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \), e per farlo, eseguiamo i seguenti passaggi di semplificazione:

Dopo aver semplificato la funzione, possiamo procedere al calcolo della derivata:

Si ottiene il seguente grafico per \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) sull'intervallo \([-5, 5]\):

Esempio: derivare una funzione

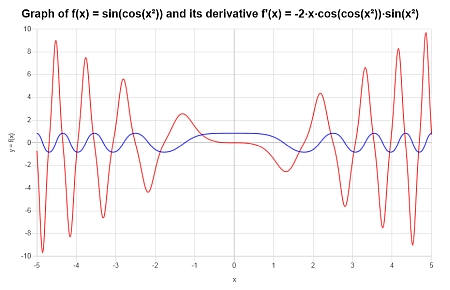
Calcola la derivata di : \(f(x) = \sin(\cos(x^2))\), e fornisci il grafico di \(f(x)\) e \(f'(x)\).

Soluzione: Ora abbiamo \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).

La funzione è già stata semplificata, quindi possiamo procedere direttamente al calcolo della sua derivata. Usando questa derivata cal otteniamo:

Pertanto, otteniamo il seguente grafico per la funzione sull'intervallo \([-5, 5]\):

Esempio: calcolatrice derivata

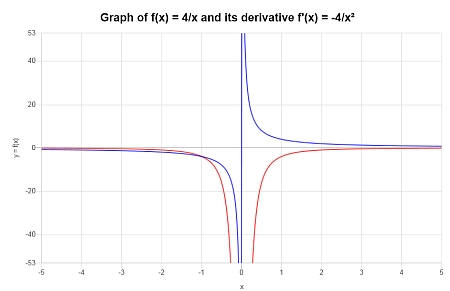
Trova la derivata di \( f(x) = \displaystyle \frac{4}{x}\). È ben definito ovunque? Grafico.

Soluzione: La funzione fornita per la quale è necessaria la derivata è \(\displaystyle f(x)=\frac{4}{x}\).

Non è necessaria alcuna ulteriore semplificazione, quindi possiamo procedere direttamente al calcolo della sua derivata:

Graficamente:

Maggiori informazioni su derivate e funzioni

Questo calcolatrice derivata con passaggi ti si rivelerà molto utile in quanto eseguirà il calcolo della derivata di una data funzione, mostrando tutti i passaggi del processo, applicando gli opportuni Regole derivate , e ti dice quando vengono applicati e perché.

Questa calcolatrice può anche essere chiamata calcolatrice dy dx O calcolatore del quoziente differenziale poiché è proprio quello che fa, calcola il limite del rapporto dy/dx quando dx si avvicina a 0.

Le funzioni sono costrutti estremamente importanti in matematica. Insieme alla differenziazione, devi essere in grado di farlo semplificare una funzione di solito, come preambolo di altri calcoli più specializzati. Esistono tipi speciali di funzioni che ti consentono di eseguire operazioni specifiche, ad esempio ciò che fai con Operazioni polinomiali .

È interessante notare che molti elementi importanti come trovare le coordinate del vertice di una parabola che può essere derivato in modo intelligente utilizzando argomenti geometrici, può essere banalmente ottenuto utilizzando la differenziazione.

Inoltre, l'idea di Linea tangente E Approssimazione Del Primo Ordine appaiono naturalmente, derivanti dal concetto di derivato, e un'estensione naturale.