Calcolatore della probabilità geometrica

Per saperne di più sul probabilità di distribuzione geometrica così puoi usare meglio questa calcolatrice.

La probabilità geometrica è un tipo di distribuzione di probabilità discreta \(X\) che può assumere valori casuali nell'intervallo \([1, +\infty)\). La variabile casuale \(X\) è il numero di prove necessarie per ottenere i primi successi.

Come si calcola la probabilità geometrica?

Per un valore \(x \in [1, +\infty)\), la probabilità geometrica viene calcolata utilizzando la seguente formula di probabilità geometrica:

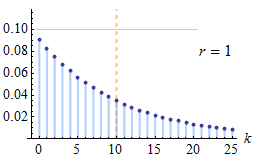
\[ \Pr(X = i) = (1-p)^{i-1} \times p \]

Utilizzando i dati di cui sopra calcolatrice della distribuzione geometrica , possiamo calcolare probabilità della forma \(Pr(a \le X \le b)\), della forma \(\Pr(X \le b)\) o della forma \(\Pr(X \ge a)\).

Digita i parametri appropriati per \(p\) nella casella di testo sopra, seleziona il tipo di code, specifica il tuo evento e calcola la probabilità geometrica desiderata.

Calcolatore della distribuzione geometrica con passaggi

Per utilizzare questo calcolatore devi sapere due cose: una è la probabilità di successo p di ogni prova. Inoltre, devi conoscere l'evento di cui vuoi calcolare la probabilità.

Ad esempio, potresti avere prove indipendenti e la probabilità di successo potrebbe essere p = 0,3, quindi esiste la tua probabilità. Quindi, potresti essere interessato a conoscere la probabilità che il primo successo si verifichi tra 4 e 6 prove. Quindi, in questo caso [4, 6] è il tuo evento.

La distribuzione geometrica e la distribuzione binomiale

Forse ti starai chiedendo, questa distribuzione geometrica sembra molto simile a Distribuzione binomiale . E in una certa misura, le impostazioni sono molto simili, poiché per entrambe le distribuzioni avrai prove indipendenti, con una probabilità fissa di successo.

E sia per la distribuzione geometrica che per quella binomiale, sei interessato ai successi delle prove. Ma la differenza è che nella distribuzione geometrica vuoi sapere quante prove ci vogliono per ottenere il primo successo, mentre nella distribuzione binomiale conti quanti successi si verificano in N prove.

Qual è il valore atteso della distribuzione geometrica

I passaggi per calcolare il valore atteso della distribuzione geometrica sono molto semplici: 1) identifichi la probabilità di successo p e 2) calcoli il valore atteso calcolando l'inverso, che è \(E(X) = \frac{1}{p}\).

Ad esempio, se hai una distribuzione geometrica con una probabilità di successo pari a p = 0,1, il valore atteso corrispondente è \(E(X) = \frac{1}{p} = \frac{1}{0.1} = 10.\).

Altri calcolatori di probabilità discreti

Se invece hai bisogno di calcolare probabilità binomiali, puoi usare il nostro calcolatore binomiale Invece. Un'altra distribuzione discreta degna di nota che potrebbe interessarti è la Distribuzione binomiale negativa .

Inoltre, puoi utilizzare il nostro Calcolatore della probabilità della distribuzione di Poisson per gestire qualsiasi applicazione che coinvolga le probabilità di Poisson, che sono abbastanza comuni in molte applicazioni

Un'altra distribuzione strettamente correlata è la Distribuzione ipergeometrica , che è simile alla distribuzione binomiale, solo che nel caso dell'ipergeometrica la probabilità di successo non è fissa.