Questo calcolatore di formule di vertice

Questa calcolatrice consentirà di applicare il formula del vertice per una data funzione quadratica che fornisci. Questa funzione quadratica deve essere valida come 2x^2 + 3x + 1/3, oppure potrebbe non essere semplificata come 2x^2 - x + 5 - 3/4 x^2 +1/3, ecc. Qualsiasi va bene una funzione quadratica valida.

Una volta fornita una funzione quadratica valida, è necessario fare clic sul pulsante "Calcola" e verranno mostrati i passaggi dell'applicazione della formula del vertice, con i passaggi seguiti per calcolare il vertice della parabola.

Le funzioni quadratiche sono molto importanti nelle applicazioni in Algebra e Calcolo, e il vertice di una funzione quadratica è molto interpretabile.

Qual è la formula del vertice?

Innanzitutto, assumiamo di iniziare con una funzione quadratica e l'abbiamo semplificata in:

\[ f(x) = ax^2 + bx + c \]

Quindi, la formula del vertice per la coordinata x del vertice è:

\[ x_V = \displaystyle -\frac{b}{2a}\]

Come applicare la formula del vertice?

• Passaggio 1: identificare la funzione quadratica nella sua forma semplificata. Devi avere qualcosa come f(x) = ax²+ bx + c
• Passaggio 2: dalla formula quadratica, devi identificare chiaramente cosa sono a e b
• Passo 3: Da a e b che hai identificato, inseriscili nella formula xv = -b/2a

Nota che se a = 0, allora la formula sarà indefinita, ma in questo caso a non sarà zero, dato che abbiamo una funzione quadratica, e il termine che moltiplica x² non può essere zero per essere una funzione quadratica valida.

Perché è importante trovare il vertice?

Il vertice ha una proprietà molto importante, che è il punto in cui la funzione quadratica raggiunge il minimo (quando si apre verso l'alto quando a > 0) oppure è il punto in cui la funzione quadratica raggiunge il massimo (quando si apre in basso quando a > 0 ).

Quindi, trovando il vertice stiamo già ottenendo il punto estremo della funzione quadratica.

Esempio: calcola vertice

Calcolare il vertice per la seguente funzione quadratica: \(f(x) = 3x^2+3x+2\)

Soluzione: Dobbiamo trovare le coordinate del vertice della funzione quadratica \(f(x) = \displaystyle 3x^2+3x+2\).

Per una funzione quadratica della forma \(f(x) = a x^2 + bx + c\), la coordinata x del vertice viene calcolata utilizzando la seguente formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In questo caso, abbiamo che la funzione per la quale dobbiamo trovare il vertice per è \(f(x) = \displaystyle 3x^2+3x+2\), il che implica che i coefficienti corrispondenti sono:

\[a = 3\] \[b = 3\] \[c = 2\]

Inserendo i valori noti di \(a\) e \(b\) nella formula per la coordinata x del vertice, otteniamo:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -\frac{1}{2}\) nella funzione quadratica, quindi otteniamo:

\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -\frac{1}{2}\) e la coordinata y del vertice è \(y_V = \displaystyle \frac{5}{4}\). Questo, il punto che rappresenta il vertice è \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

Graficamente si ottiene:

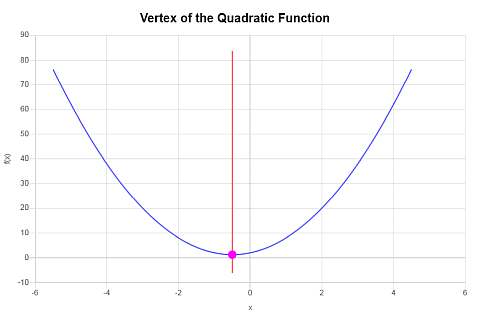
Esempio: applicazione della formula del vertice

Utilizzare la formula del vertice per calcolare le coordinate del vertice associato alla funzione \(f(x) = x^2 + 4x - \frac{3}{4}\)

Soluzione: Ancora una volta, usiamo la seguente formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Poiché \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), il che implica che i coefficienti corrispondenti sono:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

Inserendo i valori noti di \(a\) e \(b\) nella formula per la coordinata x del vertice, otteniamo:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -2\) nella funzione quadratica, quindi otteniamo:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -2\) e la coordinata y del vertice è \(y_V = \displaystyle -\frac{19}{4}\). Questo, il punto che rappresenta il vertice è \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

Questo conclude il calcolo.

Esempio: applicazione vertex

Trova il punto estremo della funzione \(f(x) = -2x^2 - 3x + 5\). Questo punto estremo è un punto di minimo o di massimo?

Soluzione: Dobbiamo trovare le coordinate del vertice della funzione quadratica \(f(x) = \displaystyle -2x^2-3x+5\).

Usiamo la seguente formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In questo caso, abbiamo che la funzione di cui dobbiamo trovare il vertice è \(f(x) = \displaystyle -2x^2-3x+5\), quindi:

\[a = -2\] \[b = -3\]

Ciò significa che:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -\frac{3}{4}\) nella funzione quadratica, quindi otteniamo:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -\frac{3}{4}\) e la coordinata y del vertice è \(y_V = \displaystyle \frac{49}{8}\). Questo, il punto che rappresenta il vertice è \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

Nota che \(a = -2 < 0\), quindi la parabola si apre verso il basso, e il punto \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) corrisponde a un punto di massimo. Cioè, la funzione quadratica \(f(x) = \displaystyle -2x^2-3x+5\) raggiunge un massimo di \( \displaystyle \frac{49}{8}\) in \( x = -\frac{3}{4}\)

Altre calcolatrici quadratiche

Si possono fare molte cose con le funzioni quadratiche. Puoi calcolare il radici di un'equazione quadratica , puoi trova l'asse di simmetria di una funzione quadratica, e così via.

Applicando il formula del vertice è strettamente legato all'applicazione del formula quadratica e il Asse di simmetria .