Ulteriori informazioni sulle disuguaglianze quadratiche

Questo calcolo di disuguaglianze quadratiche vi fornirà le soluzioni di disuguaglianze che mostrano tutti i passaggi. Ad esempio, la disuguaglianza fornita può essere qualcosa come "x^2 - 1/2 > 0" e, in generale, le disuguaglianze quadratiche non sono troppo difficili da risolvere.

Una volta fornita una disuguaglianza valida che coinvolge espressione quadratica se si fa clic su "Calcola", vengono mostrati tutti i passaggi del calcolo, compreso un grafico delle soluzioni della disuguaglianza.

disuguaglianze quadratiche sono uno dei pochi tipi (insieme a disuguaglianze lineari ) che si garantisce la possibilità di trovare una soluzione esatta, e questo processo comporta la risoluzione di un'equazione quadratica.

Qual è la definizione di questo tipo di disuguaglianza?

Non l'abbiamo detto esplicitamente, ma è chiaro fin dal nome: una disuguaglianza quadratica è un tipo specifico di disuguaglianza in cui tutti i termini coinvolti sono polinomi di grado massimo 2. In questo contesto, un esempio è

\[\displaystyle x^2 < x - 1\]

che è quadratica per il fatto che entrambi i lati della disuguaglianza sono polinomi di ordine massimo 2. Ora, se si avesse:

\[\displaystyle x^2 < x^3 - 1\]

allora la disequazione non è più quadratica, a causa del termine \(x^3\) sul lato destro. Per queste disequazioni abbiamo una chiara tabella di marcia per trovare la soluzione.

Fasi di risoluzione delle disequazioni quadratiche

• Passo 1: Assicuratevi di avere una disuguaglianza quadratica, poiché il metodo utilizzato in questo caso è valido solo per questo tipo di disuguaglianza
• Passo 2: Come per la maggior parte delle disuguaglianze, si passa tutto al lato sinistro della disuguaglianza e si risolve l'equazione associata
• Passaggio 3: Se l'equazione quadratica associata non ha radici reali, sappiamo che o l'intera retta reale è una soluzione, oppure non c'è soluzione. Quindi si testa un punto qualsiasi e si vede se risolve la disequazione; se lo fa, la soluzione è l'intera retta reale (-∞, ∞), altrimenti la soluzione è vuota.
• Passaggio 4: Se l'equazione quadratica associata ha una sola soluzione reale, significa che il grafico della quadratica associata tocca tangenzialmente l'asse delle ascisse. Quindi, a seconda del segno della disuguaglianza, la soluzione può essere solo il punto di contatto, oppure tutto tranne il punto di contatto, oppure l'intera retta reale (-∞, ∞), per la quale è necessario verificare il punto di contatto e un punto al di fuori di esso (a sinistra e a destra del punto)
• Passaggio 4: Se l'equazione quadratica associata ha due diverse soluzioni reali, si controllano gli intervalli definiti da queste radici per determinare quali porzioni della retta reale faranno parte della soluzione

Una volta analizzati i pezzi, se necessario, li si unisce utilizzando l'operatore "union", che serve a mettere insieme gli intervalli.

Come si disegna una disuguaglianza quadratica?

Grafica delle disuguaglianze fornisce un ottimo modo per capire visivamente come appare la soluzione. Per quanto riguarda la procedura, è necessario sapere se si sta lavorando con una disequazione a una sola variabile o con più variabili.

Se si ha una disuguaglianza come

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

si ha una sola variabile, e allora la soluzione sarà un sottoinsieme della retta reale. D'altra parte, se si avesse qualcosa come

\[\displaystyle y < x^2 - \frac{1}{2} x \]

allora si hanno solo due variabili x e y e quindi la soluzione della disequazione sarà un sottoinsieme del piano x-y.

Importanza delle espressioni quadratiche

Le espressioni quadratiche coinvolte in equazioni e disuguaglianze svolgono un ruolo fondamentale in matematica. Forse la quadratica è il tipo di struttura più utilizzato dopo quella lineare.

Quando si ha a che fare con il calcolo e l'algebra, si trovano innumerevoli applicazioni dei quadratici in problemi di massimizzazione e minimizzazione, integrazione e molto altro. Scavando un po', si trovano applicazioni di espressioni quadratiche in tutte le discipline scientifiche

Esempio: disuguaglianze quadratiche

Risolvere questa disequazione quadratica: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Soluzione:

Dobbiamo prima risolvere la seguente equazione quadratica ausiliaria \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\).

Applicazione della formula quadratica

L'equazione quadratica è:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In questo caso, abbiamo:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

Inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

allora, troviamo che:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Punti critici

L'elenco dei punti critici trovati è organizzato in ordine crescente: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Occorre poi analizzare i seguenti intervalli critici:

- Per l'intervallo \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): il lato sinistro è positivo, quindi \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) non fa parte della soluzione.

- Per l'intervallo \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): il lato sinistro è negativo, il che implica che \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) è una parte della soluzione.

- Per l'intervallo \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\): il lato sinistro è positivo, il che significa che \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) non fa parte della soluzione.

Soluzione

Sulla base della disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Utilizzando la notazione per intervalli, la soluzione si scrive come:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]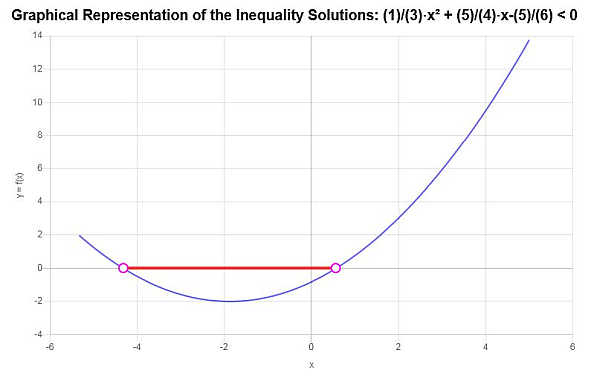

Esempio: altre disuguaglianze quadratiche

Risolvere: \(x^2 < 4\)

Soluzione:

La disuguaglianza data è:

\[x^2 < 4\]

che deriva dall'equazione quadratica \(\displaystyle x^2-4=0\).

Formula quadratica

Per un'equazione quadratica della forma \(a x^2 + bx + c = 0\), le radici vengono calcolate con la seguente formula formula quadratica :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In questo caso, abbiamo che l'equazione da risolvere è \(\displaystyle x^2-4 = 0\), il che implica che i coefficienti corrispondenti sono:

\[a = 1\] \[b = 0\] \[c = -4\]

Innanzitutto, calcoleremo il discriminante per valutare la natura delle radici. La discriminante è calcolata come:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Poiché in questo caso otteniamo che il discriminante è \(\Delta = \displaystyle 16 > 0\), che è positivo, sappiamo che l'equazione ha due radici reali diverse.

Ora, inserendo questi valori nella formula per le radici otteniamo:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

allora, troviamo che:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

In questo caso, l'equazione quadratica \( \displaystyle x^2-4 = 0 \), ha due radici reali, quindi:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

quindi il polinomio originale viene scomposto come \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \), che completa la fattorizzazione.

Analisi dei punti critici

L'elenco dei punti critici trovati è organizzato in ordine crescente: \(-2\), \(2\).

Su questa base, dobbiamo analizzare i seguenti intervalli:

- Per l'intervallo \(\left(-\infty, -2\right)\): il lato sinistro è positivo, quindi \(\left(-\infty, -2\right)\) non fa parte della soluzione.

- Per l'intervallo \(\left(-2, 2\right)\): il lato sinistro è negativo, quindi \(\left(-2, 2\right)\) fa parte della soluzione.

- Per l'intervallo \(\left(2, \infty\right)\): il lato sinistro è positivo, il che significa che \(\left(2, \infty\right)\) non fa parte della soluzione.

Soluzione alla disuguaglianza

Sulla base della disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(-2< x \le 2\).

Utilizzando la notazione per intervalli, la soluzione si scrive come:

\[\left[-2,2\right)\]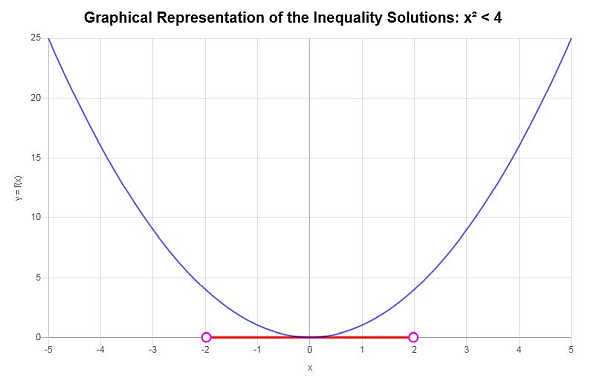

Altre utili calcolatrici di disuguaglianza

Il tipo di disuguaglianza più semplice che sarete in grado di risolvere è disuguaglianze lineari . Dopo di che, si hanno le disuguaglianze quadratiche, in termini di facilità.

Poi, avete disuguaglianze polinomiali in generale, con grado superiore a 2. Dovrebbero essere semplici, ma potrebbero comunque essere compiti formidabili in termini di quantità di lavoro necessario per risolverli.

Avere un calcolatore di disuguaglianza per le disuguaglianze in generale può essere davvero utile, in quanto affronta i diversi tipi di disuguaglianze che si prestano alla ricerca di soluzioni esatte.