Calcolatore di disuguaglianza
Istruzioni: Utilizzare la calcolatrice di disuguaglianze per risolvere qualsiasi disuguaglianza fornita, mostrando tutti i passaggi. Digitare la disuguaglianza che si desidera risolvere nella casella sottostante:
Ulteriori informazioni sulla risoluzione delle disuguaglianze
Con questa calcolatrice è possibile risolvere le disuguaglianze fornite dall'utente. Tutto ciò che dovete fare è digitare la disuguaglianza desiderata nella casella e assicurarvi di fornire una disuguaglianza valida.
Ad esempio, si può fornire qualcosa come "2x^2 - x >= 1/2", o qualcosa come "sin(x) > 0", purché si forniscano valori validi. Assicuratevi inoltre di utilizzare un segno di disuguaglianza, come ">", "<", ">=" o "<=".
Se invece si usa "=", questa calcolatrice agirà come un calcolatore di equazioni .
Una volta fornita una disuguaglianza valida, il passo successivo è fare clic su "Risolvi" e in una frazione di secondo vi verrà presentata la soluzione passo-passo. Un'avvertenza: non tutte le disuguaglianze potranno essere risolte, quindi tenetelo presente.
Non tutte le disuguaglianze sono facili da risolvere, né possiamo applicare alcuni metodi preconcetti. Solo alcuni tipi, come disuguaglianze lineari , disuguaglianze quadratiche O uguaglianze polinomiali (per i gradi inferiori) ammettono un trattamento sistematico.

Che cos'è una disuguaglianza?
Una disuguaglianza è un tipo di oggetto matematico molto simile a un oggetto equazione matematica con la differenza che invece di "=", una disuguaglianza contiene ">", "<", ">=" o "<=". Questa piccola differenza nell'aspetto aggiunge comunque più complessità alla risoluzione di una disuguaglianza rispetto a un'equazione.
Ad esempio, l'espressione seguente è una disuguaglianza
\[\displaystyle x + \frac{1}{3} < x^2 \]Si tratta quindi di un'espressione matematica che ha due lati, il lato sinistro e il lato destro, e ha "<" come segno di disuguaglianza corrispondente. La disuguaglianza di cui sopra si dice che è una disuguaglianza quadratica, perché le espressioni sui lati sinistro e destro sono entrambe polinomiali e il grado più alto è 2.
Ad esempio, la disuguaglianza che segue è una disuguaglianza trigonometrica:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]Si tratta di una disuguaglianza perché ha il segno di disuguaglianza \(\le\), e la parte destra contiene una espressione trigonometrica . Si osservi che la prima disuguaglianza è abbastanza semplice da risolvere, mentre l'altra è tutt'altro che facile e non si riesce a risolverla.
Come risolvere una disuguaglianza
In termini generali, troveremo la soluzione alle disuguaglianze risolvendo prima un'equazione associata. La soluzione della disequazione sarà più difficile se l'equazione associata è più difficile da risolvere. I seguenti passaggi vi aiuteranno nel processo di soluzione:
- Passaggio 0: Semplificare le espressioni coinvolti nella disuguaglianza. È quasi sempre più facile risolvere una disequazione semplificata che la disequazione originale
- Passo 1: Identificate la disuguaglianza che volete risolvere e identificate attentamente il segno della disuguaglianza (>, ≥, <, ≤). Se è presente il segno "=", è necessario utilizzare un segno calcolatore di equazioni invece
- Passo 2: Si scrive quindi l'equazione associata, che si ottiene semplicemente sostituendo il segno di disuguaglianza trovato nel passaggio precedente e sostituendolo con il segno di uguaglianza "="
- Passaggio 3: Risolvere l'equazione associata. Determinerete la soluzione della disequazione basandovi sull'esistenza di soluzioni reali dell'equazione associata e prendendo nota di tutti i punti che possono rendere l'espressione indefinita
- Passaggio 4: Se l'equazione associata non ha soluzioni reali: In questo caso, si sa che l'equazione non è mai nulla, almeno per valori reali. Quindi, assumendo la continuità, o tutti i punti sono una soluzione della disequazione o non lo è nessuno. Quindi si valuta la disequazione in un punto qualsiasi (ad esempio x = 0) e se vale, allora tutti i valori reali sono soluzione della disequazione, mentre se non vale, allora non ci sono soluzioni reali
- Passaggio 5: Infine, supponiamo che esistano soluzioni reali all'equazione associata. Le chiameremo punti critici e aggiungeremo all'elenco dei punti critici tutti i punti in cui l'espressione diventa indefinita (divisioni per zero, ecc.)
- Passaggio 6: Se c'è un solo punto critico, che chiamiamo "a": valutate la disuguaglianza in qualsiasi punto a sinistra di "a" e, se è valida, l'intervallo (-∞, a) farà parte dell'insieme delle soluzioni. Se la disuguaglianza è "<=" or ">=", allora si include il punto finale Infine, (-∞, a). Si fa un passo analogo per un punto a destra di 'a' e se la disuguaglianza vale per esso, allora (-∞, a) farà parte dell'insieme soluzione
- Passaggio 7: Un processo analogo viene eseguito se esistono più punti critici: Prendiamo due punti critici consecutivi, che chiamiamo "a1" e "a2": Valutare la disuguaglianza in qualsiasi punto compreso tra a1 e a2 e, se è valida, l'intervallo (a1, a2) farà parte dell'insieme soluzione. Se la disuguaglianza è "<=" or ">=", allora si includono i punti finali
Sembra complicato, ma basta essere sistematici. Per esempio, se la disuguaglianza è \(\displaystyle x + \frac{1}{3} < x^2 \), l'equazione associata è \(\displaystyle x + \frac{1}{3} = x^2 \), che è facile da risolvere, dato che è un'equazione Equazione quadrata .
Poi, nel contesto dell'analisi dei punti critici (se esistono), soluzione del grafico della disuguaglianza potrebbe rendere le cose più chiare. In alcuni corsi di Algebra insegnano agli studenti a utilizzare una tabulazione per tenere traccia di ciò che accade tra i punti critici, il che potrebbe essere molto utile.
Qual è la differenza con un sistema di disuguaglianze?
Un sistema di disequazioni consiste in diverse disequazioni simultanee che devono essere risolte contemporaneamente. Sembra più difficile della risoluzione di una semplice disequazione perché è più difficile. Se la risoluzione di una disequazione può essere laboriosa, lo è ancora di più quella di un sistema di disequazioni.
Di seguito è riportato un esempio di sistema di disuguaglianze:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]Nell'esempio precedente si ha di un sistema di disuguaglianze da risolvere. Questo sistema di disequazioni presenta due disequazioni e due incognite (x e y).
Come è facile immaginare, la risoluzione di un sistema di disuguaglianze può essere difficile in generale. Per lo più ci concentreremo sulla risoluzione di sistemi di equazioni lineari, che sono strettamente legati a risolvere un sistema di equazioni lineari

Vantaggi dell'utilizzo di questa calcolatrice di disuguaglianza con passaggi
In realtà, risolvere la maggior parte delle disuguaglianze sarà difficile. Solo alcune di esse, con strutture molto specifiche, si prestano a essere analizzate. La maggior parte non lo farà, quindi è meglio essere preparati a questo.
- Vantaggio 1: Risparmia molto tempo: La risoluzione delle disequazioni può richiedere molto tempo, poiché è necessario prima risolvere l'equazione associata e poi analizzare i punti critici
- Vantaggio 2: Assicuratevi di dare il massimo per risolverla: Come probabilmente saprete, non tutte le equazioni o disequazioni possono essere risolte facilmente, o risolte del tutto. Una calcolatrice con passaggi tenterà il miglior approccio possibile in base alla struttura rilevata
- Vantaggio 3: Ottenete i risultati, passo dopo passo, in modo ordinato. Alcune calcolatrici forniscono la risposta finale ma non mostrano i passaggi. Anche un grafico che illustra le soluzioni è utile
Mentre si impara il mestiere, avere una calcolatrice di disuguaglianze che fa il lavoro pesante per voi vi mostrerà il modo in cui le cose vengono fatte e probabilmente acquisirete le competenze necessarie per individuare le strutture più facili da affrontare.
Esiste un'utilità pratica per le disuguaglianze?
Ci puoi scommettere! Nella matematica di base (Algebra e Calcolo 101), l'enfasi è maggiore sulle uguaglianze e sulle equazioni. Il mondo reale è pieno di processi in cui non abbiamo necessariamente equazioni, ma abbiamo disuguaglianze che derivano da limiti inferiori o superiori imposti da alcuni vincoli fisici.
Alcuni campi matematici avanzati, come le equazioni differenziali, basano i loro quadri teorici sulle disuguaglianze (che gli esperti amano chiamare "stime di energia" in alcuni contesti).
L'importanza delle disuguaglianze potrebbe non essere evidente, né la necessità di impararle troppo urgente, ma in realtà le disuguaglianze costituiscono una delle pietre miliari della metodologia matematica utilizzata per costruire le teorie, anche se nei bei risultati finali tendiamo a vedere invece le uguaglianze.

Esempio: risolvere disuguaglianze
Calcolare la soluzione di: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Soluzione: Dobbiamo mettere tutti i termini della disuguaglianza sul lato sinistro (potrebbe essere il lato destro, ma è piuttosto convenzionale usare il lato sinistro):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]Dalla disuguaglianza di cui sopra, si ottiene l'equazione lineare associata che deve essere risolta per prima:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Passaggio 0: In questo caso, dobbiamo prima semplificare l'equazione lineare data e per farlo eseguiamo i seguenti passaggi di semplificazione:
Risolvere l'equazione lineare
Ponendo \(x\) sul lato sinistro e la costante sul lato destro otteniamo
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Ora, risolvendo per \(x\), dividendo entrambi i membri dell'equazione per \(\frac{1}{3}\), si ottiene quanto segue
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]e semplificando si ottiene la seguente formula
\[\displaystyle x=-\frac{13}{4}\]Pertanto, la soluzione di \(x\) per l'equazione lineare data porta a \(x=-\frac{13}{4}\).
Analisi dei punti critici
L'unico punto critico trovato è \(-\frac{13}{4}\).
Su questa base, dobbiamo analizzare i seguenti intervalli:
- Per l'intervallo \(\left(-\infty, -\frac{13}{4}\right)\): il lato sinistro è negativo, quindi \(\left(-\infty, -\frac{13}{4}\right)\) non fa parte della soluzione.
- Per l'intervallo \(\left(-\frac{13}{4}, \infty\right)\): il lato sinistro è positivo, il che significa che \(\left(-\frac{13}{4}, \infty\right)\) fa parte della soluzione.
Soluzione alla disuguaglianza
Sulla base della disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(x \ge -\frac{13}{4}\).
Utilizzando la notazione per intervalli, la soluzione si scrive come:
\[\left[-\frac{13}{4},\infty\right)\]Il grafico di disuguaglianza lineare della soluzione ottenuta è mostrato di seguito
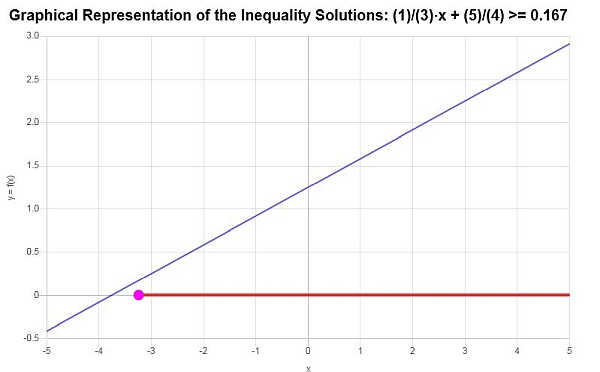
Esempio: altri esempi di disuguaglianza
Trovare la soluzione del seguente problema: \(\sin(x) > 0\)
Soluzione: Ci viene data la seguente disuguaglianza trigonometrica che deve essere risolta:
\[\sin\left(x\right) > 0\]Gestione di un'equazione ausiliaria
Dalla disuguaglianza trigonometrica di cui sopra, otteniamo l'equazione associata che dobbiamo prima risolvere:
\[\sin\left(x\right)=0\]Risoluzione dell'equazione trigonometrica ausiliaria
quindi le soluzioni sono: \(x = \pi{}K\), per una costante intera arbitraria \(K\).
Analisi dei punti critici
Sulla base delle soluzioni dell'equazione ausiliaria, l'elenco dei punti critici trovati è: \(\pi{}K\), per una costante intera arbitraria \(K\).
Si noti che abbiamo un numero infinito di intervalli critici, quindi ne analizziamo alcuni di seguito:
- Per l'intervallo \(\left(-3\pi{}, -2\pi{}\right)\): il lato sinistro è negativo, quindi \(\left(-3\pi{}, -2\pi{}\right)\) non fa parte della soluzione.
- Per l'intervallo \(\left(-2\pi{}, -\pi{}\right)\): il lato sinistro è positivo, il che significa che \(\left(-2\pi{}, -\pi{}\right)\) fa parte della soluzione.
- Per l'intervallo \(\left(-\pi{}, 0\right)\): il lato sinistro è negativo, il che significa che \(\left(-\pi{}, 0\right)\) non fa parte della soluzione.
- Per l'intervallo \(\left(0, \pi{}\right)\): il lato sinistro è positivo, il che significa che \(\left(0, \pi{}\right)\) fa parte della soluzione.
- Per l'intervallo \(\left(\pi{}, 2\pi{}\right)\): il lato sinistro è negativo, quindi \(\left(\pi{}, 2\pi{}\right)\) non fa parte della soluzione.
- Per l'intervallo \(\left(2\pi{}, 3\pi{}\right)\): il lato sinistro è positivo, il che significa che \(\left(2\pi{}, 3\pi{}\right)\) fa parte della soluzione.
E così si procede per l'intera sequenza di intervalli.
Intervalli di soluzione delle parti
Sulla base dell'analisi dei punti critici trovati e dei corrispondenti intervalli generati da punti critici consecutivi, siamo in grado di identificare i seguenti elementi come parte della soluzione della disequazione:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]In questo caso, possiamo identificare approssimativamente diverse aree di soluzione, come mostrato nel grafico seguente. Il graficatore di disuguaglianze produce la seguente rappresentazione grafica della soluzione trovata:
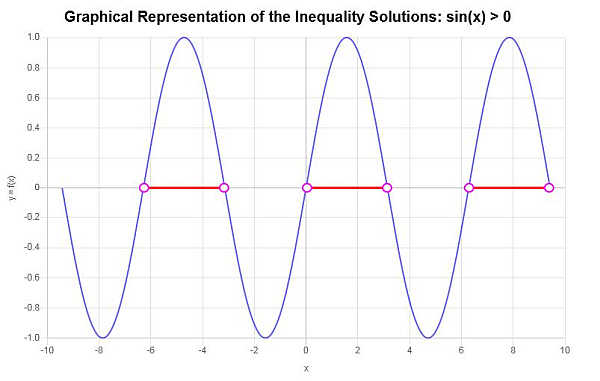
Esempio: altre disuguaglianze
Risolvere la disequazione quadratica \( x^2 - 2x > 6 \).
Soluzione: La disuguaglianza da risolvere è
\[x^2-2x > 6\]Mettendo da una parte tutti i termini della disuguaglianza, si ottiene:
\[x^2-2x-6>0\]Equazione ausiliaria
Si ottiene la seguente equazione ausiliaria, che deve essere prima risolta:
\[x^2-2x-6=0\]Abbiamo un'espressione polinomiale sul lato sinistro, che è \(\displaystyle deg(p) = 2\), il suo coefficiente principale è \(\displaystyle a_{2} = 1\) e il suo coefficiente costante è \(\displaystyle a_0 = -6\).
Formula quadratica
In questo caso, le radici vengono calcolate con la seguente formula:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]allora, troviamo che:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]In questo caso, l'equazione quadratica \( \displaystyle x^2-2x-6 = 0 \), ha due radici reali, che diventano punti critici:
Analisi dei punti critici
L'elenco dei punti critici trovati è organizzato in ordine crescente: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
Su questa base, dobbiamo analizzare i seguenti intervalli:
- Per l'intervallo \(\left(-\infty, -\sqrt{7}+1\right)\): il lato sinistro è positivo, il che implica che \(\left(-\infty, -\sqrt{7}+1\right)\) fa parte della soluzione.
- Per l'intervallo \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): il lato sinistro è negativo, quindi \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) non fa parte della soluzione.
- Per l'intervallo \(\left(\sqrt{7}+1, \infty\right)\): il lato sinistro è positivo, il che significa che \(\left(\sqrt{7}+1, \infty\right)\) è una parte della soluzione.
Trovare la soluzione alla disuguaglianza
In base alla disuguaglianza fornita e analizzando i punti critici, troviamo che la soluzione della disuguaglianza è: \(x < -\sqrt{7}+1\) o \(x > \sqrt{7}+1\).
Utilizzando la notazione per intervalli, la soluzione si scrive come:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]La soluzione della disequazione mostrata graficamente:
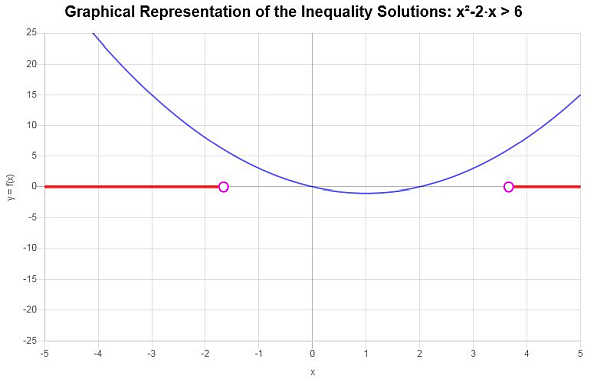
Più sopra le disuguaglianze
Si inizierà sempre con un calcolatrice per disuguaglianze lineari o forse un calcolatrice per disuguaglianze quadratiche perché sono quelli che garantiscono una soluzione.
Poi, anche con un disuguaglianza polinomiale potrebbe essere un colpo di fortuna, perché anche le disuguaglianze polinomiali possono essere complicate o addirittura impossibili da risolvere esattamente con metodi elementari.
Qualsiasi altro tipo di disuguaglianza dipenderà dalla sua struttura e da qualche abile sostituzione che si potrebbe fare.




