Ulteriori informazioni su questa calcolatrice per disuguaglianze lineari

Questa calcolatrice fornisce gli strumenti necessari per affrontare le disuguaglianze lineari. In particolare, sarete in grado di risolverle e di tracciarne il grafico, ottenendo tutti i passaggi illustrati.

Sono ammesse disuguaglianze lineari come "2x + 3 < 1" o "3x + 2y <=1" e, a seconda del numero di variabili, si otterrà un grafico adatto insieme ai passaggi che portano alla soluzione.

Una volta fornita una disuguaglianza lineare valida, è sufficiente fare clic su "Risolvi" per avviare il processo. Se c'è qualcosa di sbagliato o mancante, la calcolatrice ve lo dirà.

Questo tipo di disuguaglianze sono le più semplici e sono sempre relativamente facili da risolvere. Questo tipo, insieme a disuguaglianze quadratiche sono tra le uniche disuguaglianze "facili" da risolvere.

Che cos'è una disuguaglianza lineare?

Una disuguaglianza lineare è il tipo più semplice di disuguaglianza, in cui tutti i termini coinvolti sono lineari o costanti.

\[\displaystyle a x + b y \le 1\]

Ad esempio, l'equazione precedente è un'equazione lineare a due variabili. Tecnicamente parlando, si ha disuguaglianza polinomiale di grado 1, ma questo è un modo eccessivamente complicato di vedere la cosa.

Come si risolve una disequazione lineare?

• Passo 1: Mettete da una parte tutto ciò che contiene la variabile che volete risolvere e dall'altra il resto
• Passo 2: Gruppo e semplificare l'espressione , in modo da ridurre i termini simili
• Passaggio 3: Se una costante diversa da uno moltiplica la variabile per cui si vuole risolvere, dividere per essa. Un'avvertenza: se si divide per un valore negativo, è necessario cambiare la direzione della disuguaglianza

Uno dei punti principali da tenere a mente, e che differenzia i processi di risoluzione delle equazioni e delle disequazioni, è che quando risolviamo le equazioni possiamo moltiplicare (o dividere) più liberamente per le costanti e non cambia nulla, mentre con le disequazioni dobbiamo fare più attenzione, perché moltiplicare (o dividere) per le costanti negative cambia la direzione della disequazione.

Qual è la disuguaglianza lineare più generale?

Il massimo che si può ottenere con il lineare è

\[\displaystyle a x + bx \le c\]

ma si potrebbe avere '<' al posto di '\(\le\)'. Oppure potremmo avere

\[\displaystyle a x + bx \ge c\]

ma si potrebbe anche usare '>' invece di '\(\ge\)'.

Simile a quanto è successo con l'addizione e la sottrazione, la divisione delle frazioni è semplicemente derivata dalla moltiplicazione delle frazioni: per dividere due frazioni, devi semplicemente moltiplicare la prima per il frazione inversa della seconda (la frazione inversa si ottiene scambiando il numeratore con il denominatore nella frazione).

Applicazioni

Le disuguaglianze lineari trovano molte applicazioni in matematica. Una disuguaglianza lineare è un tipo di media ponderata, molto adatta a tutti i tipi di problemi di mescolanza e di assegnazione.

Quando si affrontano i problemi con le parole, di solito si trovano equazioni lineari, ma non è raro avere a che fare anche con disuguaglianze lineari.

Una delle aree più note è quella dell'ottimizzazione e della programmazione lineare, in cui le disuguaglianze lineari giocano un ruolo cruciale, sia con il metodo Simplex sia con le condizioni di Kuhn-Tucker quando si ha a che fare con una funzione obiettivo non lineare.

Esempio: risolvere disuguaglianze

Risolvere la seguente disequazione lineare: \(\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}\)

Soluzione:

Dobbiamo mettere da parte tutti i termini della disuguaglianza:

\[\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0\]

Equazione ausiliaria associata

Abbiamo bisogno di risolvere:

\[\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0\]

Passaggio 0: In questo caso, dobbiamo prima semplificare l'equazione lineare data e per farlo eseguiamo i seguenti passaggi di semplificazione:

Risolvere l'equazione lineare

Ponendo \(x\) sul lato sinistro e la costante sul lato destro otteniamo

\[\displaystyle \frac{2}{3}x = -\frac{17}{12}\]

Ora, risolvendo per \(x\), dividendo entrambi i membri dell'equazione per \(\frac{2}{3}\), si ottiene quanto segue

\[\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}\]

e semplificando si ottiene la seguente formula

\[\displaystyle x=-\frac{17}{8}\]

Pertanto, la soluzione di \(x\) per l'equazione lineare data porta a \(x=-\frac{17}{8}\).

Punti critici

Come previsto per una disuguaglianza lineare, esiste un solo punto critico, che è \(-\frac{17}{8}\), dal quale analizziamo i seguenti intervalli:

- Per l'intervallo \(\left(-\infty, -\frac{17}{8}\right)\): il lato sinistro è negativo, il che significa che \(\left(-\infty, -\frac{17}{8}\right)\) fa parte della soluzione.

- Per l'intervallo \(\left(-\frac{17}{8}, \infty\right)\): il lato sinistro è positivo, il che implica che \(\left(-\frac{17}{8}, \infty\right)\) non fa parte della soluzione.

Soluzione alla disuguaglianza

Si trova quindi che la soluzione della disequazione è: \(x < -\frac{17}{8}\).

L'espressione della soluzione con notazione a intervalli, la soluzione si scrive come:

\[\left(-\infty,-\frac{17}{8}\right)\]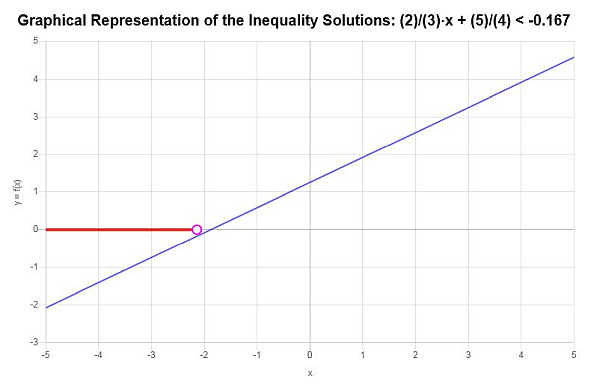

Esempio: altre disuguaglianze lineari

Risolvere questa disequazione lineare a 2 variabili: \(\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}\)

Soluzione:

Abbiamo bisogno di risolvere:

\[\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}\]

Abbiamo una disuguaglianza lineare e dobbiamo risolvere la variabile \(y\).

In questo caso, risolviamo per \(y\), quindi mettendolo da una parte della disuguaglianza e il resto dall'altra otteniamo:

\[\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}\]

Per risolvere \(y\), dividiamo entrambi i lati della disuguaglianza per \(\frac{5}{4}\), ottenendo così il risultato finale:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

Soluzione di una disuguaglianza lineare

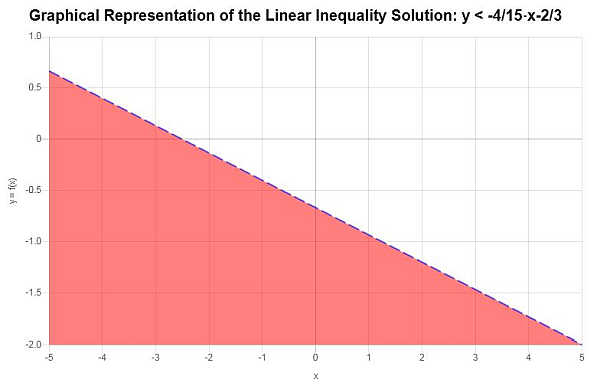
In base alla disuguaglianza fornita, dopo averla risolta per \(y\) otteniamo:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

La rappresentazione grafica della regione di soluzione è riportata nel grafico seguente:

Altri calcolatori di algebra

La gestione dell'espressione è fondamentale in Algebra. Semplificazione dell'espressione è l'inizio della maggior parte dei processi matematici e di solito è necessario ridurre le cose alla loro espressione più semplice.

Risolvere le equazioni e anche Risolvere le disuguaglianze rimarrà al centro della maggior parte dei processi, poiché l'uno o l'altro saranno al centro di quasi tutto ciò che si fa in matematica.