En savoir plus sur la formule de la pente

Cette Formule de la pente vous permettra de calculer la pente pour deux points donnés de la forme (x, y) en utilisant la formule bien connue, en montrant toutes les étapes.

Vous devez fournir deux points de la forme (x, y). Par exemple, vous pouvez fournir des points comme (1/2, 1/3), ou quelque chose qui n'est pas simplifié comme (1/3+1/4, sqrt(8)).

Une fois que vous avez fourni deux points valides de la forme (x, y), l'étape suivante consiste à cliquer sur le bouton "Calculer", et vous obtiendrez toutes les étapes de calcul de la formule de pente.

Le concept de pente est un concept crucial en algèbre et en géométrie, et la pente est très importante pour la construction d'une fonction linéaire .

Quelle est la formule de la pente ?

Supposons que nous ayons deux points \((x_1, y_1)\) et \((x_2, y_2)\) sur le plan. Alors le Formule de la pente is :

\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]

Certaines personnes diront "c'est le rapport entre la différence des y et la différence des x", avec la réserve que vous devez préserver l'ordre lorsque vous faites les différences. Si en haut vous faites \(y_2 - y_1\), alors en bas vous faites \(x_2 - x_1\) et non \(x_1 - x_2\).

Certains appellent cette formule de pente "Rise versus Run"/..

Quelles sont les étapes de l'utilisation de la formule de la pente ?

• Étape 1 : Identifiez les deux points donnés. Il est bon de simplifier les expressions autant que possible, avant d'utiliser la formule suivante
• Étape 2 : Déterminez lequel est le premier point, et lequel est le second. Le choix n'a pas d'importance pour le résultat, à condition que vous restiez cohérent avec votre choix
• Étape 3 : Utilisez la formule \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\) en branchant les valeurs du premier point \(x_1\) et \(y_1\), et du deuxième point \(x_2\) et \(y_2\)
• Étape 4 : Après avoir entré les valeurs, simplifiez autant que possible pour ramener la pente à sa forme la plus simple

Le calcul de la pente à l'aide de la formule est généralement un processus très simple, il suffit de s'assurer que l'ordre des points reste cohérent.

Comment utiliser la pente ?

La pente est une mesure de l'inclinaison d'une ligne. En effet, lorsque vous avez une fonction linéaire de la forme

\[y = m x + n\]

alors, la pente de la ligne est m. Ce qui précède est connu sous le nom de Forme d'interception de pente d'une ligne.

Quelles sont les étapes pour utiliser la pente d'une ligne ?

• Étape 1 : Identifiez la pente m. Simplifiez-la autant que possible
• Étape 2 : Vous devez connaître l'ordonnée à l'origine, c'est-à-dire le point sur l'axe des y lorsque la droite le croise, et l'appeler n
• Étape 3 : Alors, l'équation de la ligne est \(y = m x + n\)

Il y a d'autres formes pour exprimer la ligne que le Interception de pente . Vous avez le forme standard de la ligne et le Forme point-pente .

Comment utiliser la formule de l'intersection des pentes

C'est le centre de fonctions linéaires (ou affine linéaire devrait-on dire) et les graphes linéaires. En effet, lorsque vous avez la pente m et l'ordonnée à l'origine n, vous calculez directement l'équation de la droite sous la forme y = mx + n.

D'un point de vue géométrique, c'est assez simple à interpréter, car l'ordonnée à l'origine est clairement le point d'intersection entre la droite et l'axe des y, et la pente est la mesure de l'inclinaison. À titre de référence, une pente de m = 1 correspond à une inclinaison de 45° ^O .

A l'inverse, si vous avez fonction linéaire par Simplification algébrique vous pouvez toujours réduire à la forme de l'ordonnée à l'origine y = mx + n, et vous avez alors trouvé la pente m et l'ordonnée à l'origine n.

Exemple : en utilisant la formule de la pente

Calculez la pente pour les points suivants : \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) et \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)

Solution: Nous devons calculer la pente d'une ligne qui passe par les points \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) et \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\).

La formule suivante est nécessaire pour calculer la pente à partir de ces deux points :

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Maintenant, en branchant les valeurs des points \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) et \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) on obtient :

On en conclut que la pente d'une droite qui passe par les points \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) et \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) est \(m = \displaystyle \frac{1}{4}\).

Exemple : autres exemples de la formule de la pente

Utilisez la formule de la pente pour trouver la pente de la droite qui passe par les points : \((2, 4)\) et \((5, 12)\)

Solution: Dans ce cas, nous avons les points \(\displaystyle (x_1, y_1) = \left(2,4\right)\) et \(\displaystyle (x_2, y_2) = \left(5,12\right)\), qui sont les points par lesquels nous savons que la ligne passe.

La formule de la pente est la suivante :

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Maintenant, en branchant les valeurs des points \(\displaystyle (x_1, y_1) = \left(2,4\right)\) et \(\displaystyle (x_2, y_2) = \left(5,12\right)\) on obtient :

On en conclut que la pente d'une droite qui passe par les points \(\displaystyle (x_1, y_1) = \left(2,4\right)\) et \(\displaystyle (x_2, y_2) = \left(5,12\right)\) est \(m = \displaystyle \frac{8}{3}\).

Exemple : forme de l'ordonnée à l'origine

Trouvez la forme de l'intercept de la pente pour la ligne suivante : \(2x + 4y = 3 + \frac{1}{2}x\).

Solution: Nous avons l'équation suivante :

\[\displaystyle 2x+4y=3+\frac{1}{2}x\]

En mettant \(y\) sur le côté gauche et \(x\) et la constante sur le côté droit, nous obtenons

\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]

Maintenant, le terme multipliant \(y\) est \( 4 - 0 = 4\), et aussi depuis \( \frac{1}{2} - 2 = -\frac{3}{2}\), on obtient ceci

\[\displaystyle 4y=-\frac{3}{2}x+3\]

Maintenant, en résolvant pour \(y\), en divisant les deux côtés de l'équation par \(4\), on obtient ce qui suit

\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]

et en simplifiant on obtient finalement ce qui suit

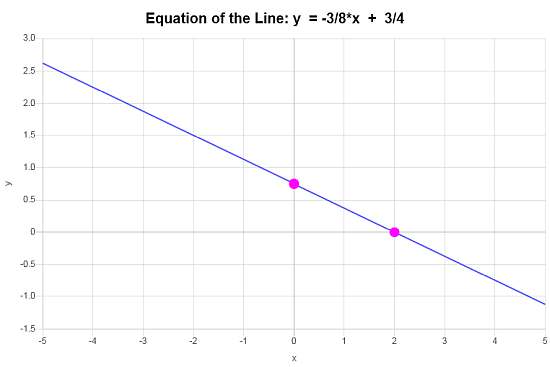
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]

Conclusion : Sur la base des données fournies, nous concluons que l'équation de la droite sous forme pente-ordonnée à l'origine est \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\), avec une pente de \(\displaystyle b = -\frac{3}{8}\) et une ordonnée à l'origine de \(\displaystyle n = \frac{3}{4}\).

Graphiquement, la ligne ressemble à :

Autres calculateurs de fonctions linéaires

Avec fonctions quadratiques les fonctions linéaires font partie des objets les plus importants en mathématiques. Vous pouvez calculer la pente d'une ligne, trouver la valeur de l'angle d'ouverture d'une ligne, etc ligne perpendiculaire et de convertir la ligne en différentes formes, selon les besoins.

Une chose qui est remarquable pour les fonctions linéaires, c'est qu'il est plus facile de trouver fonctions linéaires inverses car la plupart des fonctions linéaires sont de 1 à 1 (à l'exception des lignes horizontales).