Calculatrice de forme de point de ligne-pente
Instructions: Utilisez cette calculatrice pour trouver la forme d'interception de la pente de la ligne que vous fournissez, avec toutes les étapes indiquées. À cette fin, vous devez donner des informations sur la ligne que vous souhaitez mettre sous forme de point-pente.
Vous pouvez nous parler de votre ligne de différentes manières. Vous pouvez fournir : (1) à la fois la pente et l'ordonnée à l'origine, (2) vous pouvez saisir n'importe quelle équation linéaire (ex : \(x + 3y = 2 + \frac{2}{3}x\)), (3) vous pouvez indiquer la pente et un point où la ligne passe par, ou (4) vous pouvez indiquer deux points par lesquels la ligne passe.
À propos de ce calculateur de forme point-pente de la ligne.
Ce calculateur d'équation point-pente vous fournira un calcul étape par étape de l'équation de la ligne sous forme de point-pente pour toute ligne que vous avez initialement fournie.
Ce que vous devez faire est d'identifier la ligne avec laquelle vous souhaitez travailler. Cette ligne peut être identifiée de différentes manières et vous sélectionnerez en fonction des informations que vous avez fournies.
L'une des manières les plus courantes consiste à définir une ligne en fournissant sa pente et son Interception O , mais ce n'est certainement pas le seul moyen.
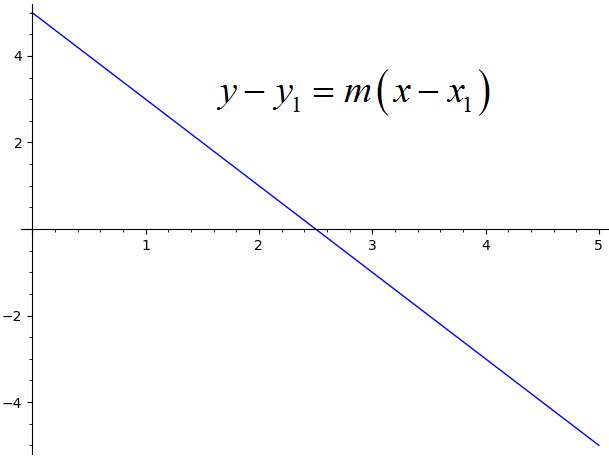
Comment représenter une droite sous forme point-pente ?
Une droite est dite sous forme point-pente si elle peut s'écrire :
\[y - y_1= m (x -x_1)\]Dans ce contexte, \(m\) est identifié comme la pente de la ligne, et \((x_1, y_1)\) est un point par lequel la ligne passe.
Comment trouver l'ordonnée à l'origine avec une calculatrice ?
Si vous connaissez la pente \(m\) de la ligne et un point \((x_1, y_1)\) où la ligne est passée, le processus est simple et direct, mais cela pourrait être plus délicat si vous avez défini la ligne en utilisant un autre type d'information.
Pourquoi la forme point-pente d'une ligne est-elle utile
La forme point-pente est utile car elle donne une interprétation directe de la pente de la ligne comme le taux de changement. En effet, directement à partir de la forme point-pente on obtient
\[\frac{y-y_1}{x-x_1} = m\]Puis-je obtenir un formulaire de pente de point avec deux points ?
Oui! Si vous avez deux points, vous les utilisez d'abord pour calculer la pente \(m\), puis choisissez l'un des points pour appliquer directement la formule
\[y - y_1= m (x -x_1)\]
Exemple : Calcul du formulaire Point-Pente
Supposons que vous sachiez que la droite passe par les points \(( \frac{1}{3}, 2)\) et \((\frac{7}{2}, 3)\). Trouvez la forme point-pente de la ligne.
Réponse:
L'information fournie sur la ligne est que la ligne passe par les points\(\displaystyle \left( \frac{1}{3}, 2\right)\) et \(\displaystyle \left( \frac{7}{2}, 3\right)\)
Par conséquent, la première étape consiste à calculer la pente. La formule de la pente est : \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]
Maintenant, en branchant les nombres correspondants est , on obtient que la pente est : \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 3 - 2}{ \displaystyle \frac{7}{2} - \frac{1}{3}} = \frac{ \displaystyle 1}{ \displaystyle \frac{19}{6}} = \frac{6}{19}\]
Alors, maintenant nous savons que la pente est \(\displaystyle m = \frac{6}{19}\) et que la droite passe par le point \(\displaystyle \left( \frac{1}{3}, 2\right)\)
Par conséquent, avec les informations dont nous disposons, nous pouvons construire directement la forme point-pente de la ligne, qui est
\[\displaystyle y - y_1 = m \left(x - x_1\right)\]puis en branchant les valeurs connues de \(\displaystyle m = \frac{6}{19}\) et \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, 2\right)\), on obtient que
\[\displaystyle y-2 = \frac{6}{19} \left(x-\frac{1}{3}\right)\]Conclusion : Sur la base des données fournies, nous concluons que l'équation de la ligne sous forme point-pente est \(\displaystyle y-2=\frac{6}{19}\left(x-\frac{1}{3}\right) \).
Vous pouvez également utiliser notre Calculateur de formulaire standard et calculatrice d'interception de pente d'une ligne, si ce sont plutôt les formats qui vous intéressent.




