En savoir plus sur ce calculateur de ligne perpendiculaire.

Les lignes sont en grande partie déterminées par leur pente (inclinaison). Les lignes horizontales sont des lignes dont la pente est égale à zéro, les lignes verticales sont des lignes dont la pente est indéfinie (infini négatif ou positif).

Les lignes perpendiculaires sont des lignes qui se croisent en formant un angle droit. Il existe une condition spécifique pour le pente et la pente perpendiculaire , chaque fois que les pentes sont définies, pour que les droites soient perpendiculaires, c'est-à-dire que le produit des pentes soit -1.

Observez qu'une droite donnée a une infinité de droites perpendiculaires. Afin de trouver celui que vous recherchez, vous devez fixer un point par lequel il passe.

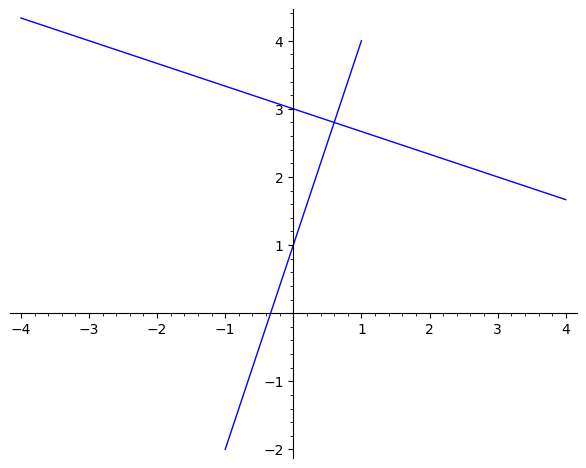
Comment trouver la perpendiculaire d'une droite ?

La stratégie est simple. L'étape consiste à trouver la pente de la droite donnée. Si vous disposez de la pente et de l'intersection pour définir la ligne, vous avez déjà la pente.

Sinon, peut-être avez-vous deux points où passe la droite , auquel cas vous pouvez calculer directement la pente.

En fin de compte, si vous définissez votre ligne donnée avec une équation, vous devez intégrer cette équation dans le Forme d'interception de pente , donc pour obtenir la pente.

Une fois que vous avez la pente de la droite donnée, vous utilisez la formule de la pente perpendiculaire, en multipliant par moins un l'inverse de la pente d'origine.

Quelle est la droite perpendiculaire d'une droite horizontale

La ligne perpendiculaire à une ligne horizontale est une ligne verticale.

Quelle est la perpendiculaire d'une verticale

La ligne perpendiculaire à une ligne verticale est une ligne horizontale.

Pouvez-vous calculer la ligne perpendiculaire sans points

Une fois que vous avez une ligne, il n'y a pas une mais plusieurs lignes perpendiculaires (infinies) à la ligne donnée. Afin d'identifier une ligne perpendiculaire spécifique, vous devez fournir un point où la ligne passe.

En règle générale, vous fournirez un point sur la ligne d'origine, où vous souhaitez que la ligne perpendiculaire passe.

Exemple de calcul d'une droite perpendiculaire pour une droite donnée :

Considérez la droite d'équation \(2x + 3y = 5)\). Trouvez l'équation de la droite perpendiculaire qui passe par \((1, 1)\).

Solution: Nous obtenons d'abord l'équation d'interception de la pente pour la ligne DONNÉE, si possible

On nous a fourni l'équation suivante :

\[\displaystyle 2x+3y=5\]

En mettant \(y\) sur le côté gauche et \(x\) et la constante sur le côté droit, nous obtenons

\[\displaystyle 3y = -2x +5\]

Ensuite, en résolvant pour \(y\), en divisant les deux côtés de l'équation par \(3\), on obtient ce qui suit

\[\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\]

Formule De Pente Perpendiculaire

En général, la formule nécessaire pour calculer la pente perpendiculaire, \(m_{\perp}\), est :

\[m_{\perp} = \displaystyle -\frac{1}{m}\]

En insérant la valeur de \(m = \) dans la formule, on trouve que la pente perpendiculaire est

\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{} = \frac{3}{2}\]

Construction En Ligne Perpendiculaire

Maintenant, nous avons calculé que la pente perpendiculaire est \(m_{\perp} = \frac{3}{2}\) et nous savons que la droite perpendiculaire passe par le point \((1, 1)\).

Par conséquent, avec les informations dont nous disposons, nous pouvons construire directement la forme point-pente de la ligne, qui est

\[\displaystyle y - y_1 = m_{\perp} \left(x - x_1\right)\]

puis en branchant les valeurs connues de \(\displaystyle m_{\perp} = \frac{3}{2}\) et \(\displaystyle \left( x_1, y_1 \right) = \left( 1, 1\right)\), on obtient que

\[\displaystyle y-1 = \frac{3}{2} \left(x-1\right)\]

Maintenant, nous devons développer le côté droit de l'équation en distribuant la pente, nous obtenons donc \[\displaystyle y = \frac{3}{2} x + \frac{3}{2} \left(-1\right) + 1\]

et en simplifiant on obtient que \[\displaystyle y=\frac{3}{2}x-\frac{1}{2}\]

Par conséquent, nous concluons que l'équation de la ligne donnée est \(\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\) et l'équation de la ligne perpendiculaire est \(\displaystyle y=\frac{3}{2}x-\frac{1}{2}\).

Si vous voulez rendre les choses plus directes, utilisez ceci Calculateur de pente perpendiculaire et utilisez la formule de la ligne perpendiculaire pour obtenir directement la pente de la ligne qui est la ligne perpendiculaire.

C'est pour le cas où vous êtes seulement à la recherche de la pente dans le cadre de ce que vous faites.