Plus d'informations sur cette ligne dans le calculateur de formulaire pente-ordonnée à l'origine

Ce calculateur d'équation de pente à l'origine vous permettra de fournir des informations sur une équation linéaire de l'une des quatre manières, puis il vous montrera comment la mettre en Forme d'interception de pente , avec la formule suivante :

\[y = ax + b\]

où a est le pente de la ligne , et b est le Interception O , et votre objectif est de trouver les deux. Plus d'informations à ce sujet ci-dessous.

Comment définissez-vous l'équation de la ligne dans cette calculatrice

Tout d'abord, vous devez fournir des informations pour spécifier l'équation. Il existe plusieurs façons de définir une équation linéaire. Une façon consiste simplement à taper directement une équation linéaire valide.

Mais d'autres fois, selon le type d'informations qui vous ont été fournies, vous pouvez avoir la pente et l'ordonnée à l'origine (qui définissent ensemble de manière univoque une ligne) ou vous pouvez également fournir la pente de la ligne et un point par lequel elle passe.

En fin de compte, vous pouvez avoir deux points par lesquels vous savez que la ligne passe, ce qui définirait également une et une seule ligne.

Donc, en fonction des informations dont vous disposez, vous devrez décider quelle option utilisez-vous pour identifier initialement votre ligne.

Comment représentez-vous une ligne au format pente-ordonnée à l'origine ?

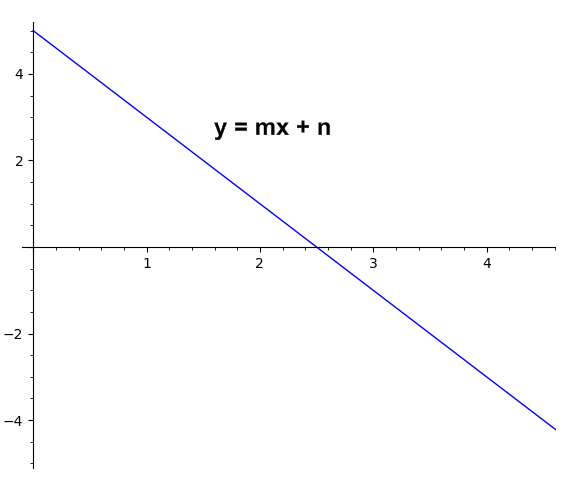
Une équation linéaire est dite sous forme pente-ordonnée à l'origine si elle a la structure suivante :

\[y = m x + n\]

Peut-être l'avez-vous vu écrit comme \(y = a + b x\), mais c'est exactement la même chose : nous avons la variable dépendante (\(y\)) d'un côté, et nous avons une constante plus une autre constante (qui peut être négative) multiplier la variable indépendante (\(x\)).

Comment arrivez-vous à l'interception de la pente sur une calculatrice ?

Avec ce solveur/calculateur, il vous suffit de fournir des informations permettant d'identifier la ligne sur laquelle vous travaillez, en utilisant l'une des quatre options différentes.

Une fois que vous avez fourni les informations initiales, la procédure pour arriver au Forme d'interception de pente dépendra de la façon dont la ligne a été initialement construite, mais l'idée est que nous résolvons pour \(y\).

Pourquoi la forme d'interception de la pente d'une ligne est-elle très couramment utilisée

L'interception de la pente d'une ligne est très couramment utilisée car elle donne une représentation très intuitive et graphique de ce que fait la ligne. Avec le Interception O nous savons où la ligne coupe l'axe y, et avec la pente nous connaissons un degré de l'inclinaison de la ligne.

Une pente négative indique une ligne descendante et une pente positive indique une ligne ascendante. Lorsque la pente est nulle, alors la droite est horizontale

De plus, mettre l'équation d'une droite sous la forme pente-ordonnée à l'origine permet de solution d'équations linéaires simultanées .

Ce solveur peut-il passer d'une forme standard à une forme d'interception de pente ?

Absolument. Si vous avez un équation sous forme standard , tout ce que vous avez à faire est de taper l'équation, de cliquer sur "Calculer" et le solveur vous montrera, étape par étape, comment arriver à la forme pente-ordonnée à l'origine.

Exemple : Calcul de la pente à l'origine

Supposons que vous ayez une ligne au format standard \( \frac{1}{3} x + \frac{4}{5} y = 2\). Trouvez la forme d'interception de la pente.

Réponse:

On nous a fourni l'équation suivante :

\[\displaystyle \frac{1}{3}x+\frac{4}{5}y=2\]

En mettant \(y\) sur le côté gauche et \(x\) et la constante sur le côté droit, nous obtenons

\[\displaystyle \frac{4}{5}y = -\frac{1}{3}x +2\]

Enfin, en résolvant pour \(y\), on obtient ce qui suit

\[\displaystyle y=\frac{-\frac{1}{3}}{\frac{4}{5}}x+\frac{2}{\frac{4}{5}}\]

et en simplifiant tous les termes qui nécessitent une simplification, on obtient finalement le résultat suivant

\[\displaystyle y=-\frac{5}{12}x+\frac{5}{2}\]

Conclusion : Sur la base des données fournies, nous concluons que l'équation de la droite sous forme pente-ordonnée à l'origine est \(\displaystyle y=-\frac{5}{12}x+\frac{5}{2}\), avec une pente de \(\displaystyle m = -\frac{5}{12}\) et une ordonnée à l'origine de \(\displaystyle n = \frac{5}{2}\).