Comment utiliser ce calculateur de pente avec étapes

Utilisez cette calculatrice pour trouver la pente d'une ligne que vous fournissez, avec toutes les étapes indiquées.

La pente est une mesure de l'inclinaison de la ligne par rapport aux axes de coordonnées. Une pente positive indique que la ligne a une inclinaison vers le haut, tandis qu'une pente négative indique que la ligne a une inclinaison vers le bas.

Une pente égale à zéro indique que la ligne est horizontale, alors qu'une ligne verticale n'a pas de pente bien définie.

Comment calculer une pente ?

Normalement, le calcul de la pente est facile, mais il y a plusieurs façons de calculer une pente, et tout dépend des informations fournies et de la façon dont elles sont fournies.

Le plus souvent, le calcul de la pente est présenté sous la forme d'une équation linéaire dont il faut trouver la pente, ou sous la forme de deux points par lesquels passe une droite.

Calculatrice de pente à partir d'une équation : trouver la pente de la droite

Cette calculatrice vous montrera comment calculer la pente d'une ligne que vous fournissez, et vous aurez différentes façons d'indiquer et de définir votre ligne. Elle vous donnera également un graphique reflétant la pente calculée.

Par exemple, une méthode courante consiste à définir votre ligne en donnant une équation, puis vous aurez cette calculatrice pour calculer la pente à partir de l'équation.

La stratégie générale pour cela est de mettre l'équation de la droite sous la forme pente-ordonnée à l'origine à partir de laquelle il est facile de reconnaître la pente à partir de la structure de l'équation \(y = mx + n\).

Il s'agit également d'une calculatrice de pente à partir de deux points

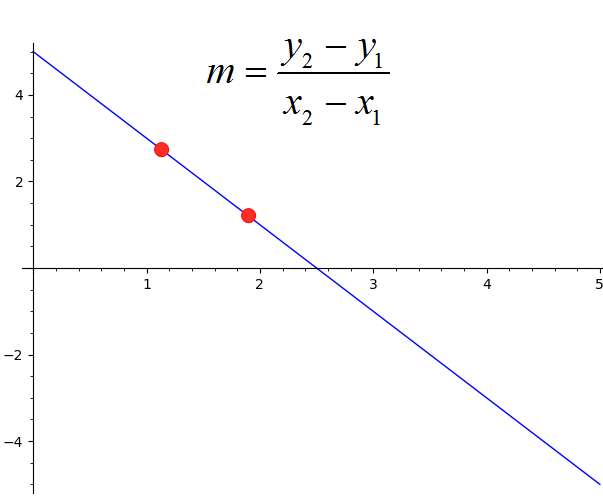
L'une des façons les plus courantes de calculer la pente consiste peut-être à définir l'équation en fournissant deux points comme \((x_1, y_1)\), \((x_2, y_2)\). Alors, comment trouver la pente à partir de deux points ? La pente est simplement calculée comme suit

\[m = \frac{y_2-y_1}{x_2-x_1}\]

qui consiste à trouver la pente à partir de deux points. N'oublions pas que ces deux points sont généralement des points de passage d'une droite, et que vous recherchez donc la pente de la droite qui passe par ces points.

En fin de compte, la façon de trouver la pente d'une ligne dépendra de la façon dont la ligne est définie. Cette calculatrice vous couvrira de tous les cas, même lorsqu'il y a des fractions dans le calcul.

Interprétation : qu'est-ce qu'une pente de 2 % ?

Il y a plusieurs façons de voir cela, mais une façon courante est de penser que pour chaque augmentation de 100 unités dans X, la ligne augmente de 2 unités dans Y, ce qui explique les 2/100 = 0,02 = 2 %.

Dans le même ordre d'idée, on peut dire qu'une pente de 45% est telle qu'une augmentation de 100 unités de X entraîne une augmentation de 45 unités de Y. Remarquez que ce n'est pas la même chose qu'une pente de 45% ^o degrés.

Calculateur de pente instantané

L'idée d'un calculateur de pente est simple lorsque l'on considère deux points, auquel cas on utilise la formule ci-dessus. Mais qu'est-ce que la pente instantanée ? Il s'agit de la pente lorsque les deux points se rapprochent de plus en plus.

Vous voulez donc voir quelle valeur la pente approche, lorsque les deux points se rapprochent l'un de l'autre. L'idée de pente instantanée se traduit par ceci calculatrice de dérivées qui consiste essentiellement à calculer des pentes instantanées.

Exemple : calcul de la pente

Supposons que vous ayez une droite ayant la forme standard suivante \( \frac{3}{4} x + 2y = 6\). Trouvez la pente de la droite.

Solution : Calcul de la pente d'une ligne

On nous a fourni l'équation suivante :

\[\displaystyle \frac{3}{4}x+2y=6\]

En plaçant \(y\) du côté gauche et \(x\) et la constante du côté droit, nous obtenons

\[\displaystyle 2y = -\frac{3}{4}x +6\]

Maintenant, en résolvant \(y\), en divisant les deux côtés de l'équation par \(2\), on obtient ce qui suit

\[\displaystyle y=-\frac{\frac{3}{4}}{2}x+\frac{6}{2}\]

et en simplifiant on obtient finalement ce qui suit

\[\displaystyle y=-\frac{3}{8}x+3\]

Conclusion : Sur la base des données fournies, nous concluons que la pente de la ligne est \(\displaystyle m = -\frac{3}{8}\).

Exemple : calcul de la pente à partir de deux points

Supposons que vous ayez une ligne qui passe par 2 points : \( (1, 2)\) et \( (4, 11/3)\). Trouvez la pente de la ligne.

Solution :

Calcul de la pente d'une ligne

L'information fournie sur la droite est qu'elle passe par les points\(\displaystyle \left( 1, 2\right)\) et \(\displaystyle \left( 4, \frac{11}{3}\right)\)

La première étape consiste donc à calculer la pente. La formule de la pente est la suivante \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]

Maintenant, en introduisant les nombres correspondants dans , nous obtenons que la pente est : \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{11}{3} - 2}{ \displaystyle 4 - 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]

On constate donc que la pente est \(\displaystyle m = \frac{5}{9}\) et que la droite passe par le point \(\displaystyle \left( 1, 2\right)\)

Conclusion : Sur la base des données fournies, nous concluons que la pente de la ligne est \(\displaystyle m = \frac{5}{9}\).

La pente d'une ligne est l'une de ses propriétés les plus importantes, avec la Interception O et abscisse à l'origine , car ils définissent essentiellement la ligne.