En savoir plus sur cette calculatrice d'équation de droite sous forme standard

Cette équation de la ligne dans le calculateur d'équation de forme standard vous permettra de définir une équation de l'une des quatre manières que vous préférez, et elle vous montrera toutes les étapes requises.

Comment trouver l'équation d'une droite ? Donc la première chose est de définir une équation linéaire. A cet effet, vous pouvez soit fournir directement une équation, soit au contraire, selon les informations dont vous disposez, vous pouvez fournir :

(1) la pente et l'ordonnée à l'origine.

Ou (2) la pente et un point où la ligne passe,

ou (3) vous pouvez fournir deux points où la ligne passe.

La méthode que vous utiliserez pour définir votre équation dépendra des informations dont vous disposez.

Quel est le format d'une équation linéaire sous forme standard ?

Une équation linéaire est dite sous forme standard si elle a la structure suivante :

\[a x + by = c\]

Ensuite, votre objectif est de déterminer la formule de forme standard et de trouver les constantes a, b et c qui la déterminent.

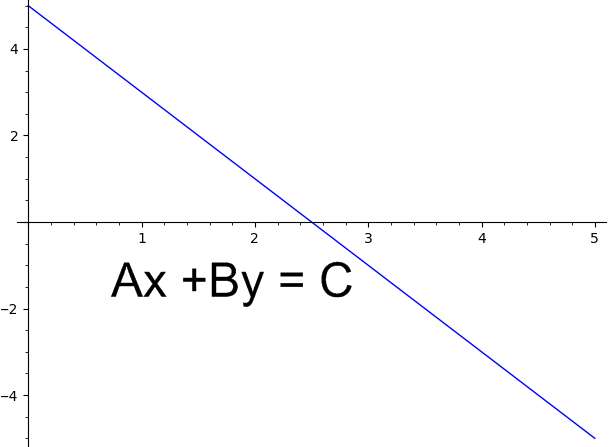
Comment résolvez-vous le formulaire standard sur une calculatrice?

Avec cette calculatrice, il vous suffit de fournir des informations pour définir l'équation, parmi les quatre options différentes.

Pourquoi le formulaire standard est-il nécessaire

Certaines formes spécifiques d'une équation viennent de la tradition, mais généralement parce qu'il est utile d'utiliser une forme spécifique.

Dans le cas de la forme standard, il est pratique de l'avoir sous la forme \(a x + by = c\), car en branchant \(x=0\) il est facile de calculer la Interception O , et en branchant \(y=0\) il est facile de calculer la abscisse à l'origine .

En outre, la forme standard est couramment utilisée comme format de choix lors de la résolution systèmes simultanés d'équations linéaires .

Ce solveur peut-il traiter des équations linéaires fractionnaires ?

L'un des avantages de cette calculatrice est que tous les coefficients que vous utilisez pour définir l'équation peuvent être n'importe lesquels. expression numérique générique , qui comprend fractions .

Pour voir un exemple de la façon dont cette calculatrice traite les équations linéaires fractionnaires, consultez l'exemple ci-dessous.

Exemple : Calcul de l'équation d'une droite

Supposons que vous ayez une droite passant par le point \(\left( \frac{1}{3}, \frac{2}{3}\right)\) avec une pente \(m = \frac{1}{2}\). Trouvez la forme standard de la ligne.

Réponse:

L'information initialement fournie sur la droite est que la pente est \(\displaystyle m = \frac{1}{2}\) et que la droite passe par le point \(\displaystyle \left( \frac{1}{3}, \frac{2}{3}\right)\)

Ainsi, avec les informations dont nous disposons, nous pouvons construire directement le forme point-pente de la ligne , lequel est

\[\displaystyle y - y_1 = m \left(x - x_1\right)\]

puis en branchant les valeurs connues de \(\displaystyle m = \frac{1}{2}\) et \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, \frac{2}{3}\right)\), on obtient que

\[\displaystyle y-\frac{2}{3} = \frac{1}{2} \left(x-\frac{1}{3}\right)\]

Maintenant, nous devons développer le côté droit de l'équation en distribuant la pente, nous obtenons donc \[\displaystyle y = \frac{1}{2} x + \frac{1}{2} \left(-\frac{1}{3}\right) + \frac{2}{3}\]

et en simplifiant on obtient que \[\displaystyle y=\frac{1}{2}x+\frac{1}{2}\]

Le passage de la variable indépendante au côté gauche de l'équation conduit à la forme standard suivante de la ligne :

\[\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\]

Conclusion : Sur la base des données fournies, nous concluons que l'équation de la ligne sous forme standard est \(\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\).

Autres calculatrices utiles liées aux fonctions linéaires

Souvent, vous voulez juste avoir un aperçu rapide de l'apparence graphique des choses, pour lesquelles vous pouvez utiliser cet outil pour représenter graphiquement des équations linéaires

Ou vous pouvez également représenter graphiquement deux équations linéaires et trouver l'intersection de deux droites , s'il existe.

Comme étape précédente, vous voudrez peut-être d'abord calculer la pente, donc pour vous le formulaire pente-ordonnée à l'origine, pour lequel vous pourriez utiliser ceci calculateur de formule de pente d'une droite .