Le domaine d'une fonction est un ensemble où une fonction est bien définie. Plus précisément, laissez \(f: D \rightarrow R\) une fonction, ce qui signifie que \(f(a)\) est bien défini pour \(a \in D\). Le domaine de la fonction \(f\) est l'ensemble \(D\).

Mathématiquement, vous écrirez \(dom(f) = D\).

La plage d'une fonction, en revanche, est un ensemble de valeurs qui peuvent être atteintes via la fonction.

Plus précisément, soit \(f: D \rightarrow R\) une fonction, la plage est l'ensemble de toutes les valeurs possibles \(b \in R\) pour lesquelles il existe \(a \in D\) tel que \(f(a) = b\).

Souvent, la plage d'une fonction est écrite sous la forme \(R(f)\) ou également sous la forme \(f(D)\) (qui est également appelée ensemble d'images de \(D\) via la fonction \(f\)).

Il est crucial de connaître le domaine d'une fonction car cela nous donne un ensemble sûr de valeurs sur lesquelles la fonction est bien définie.

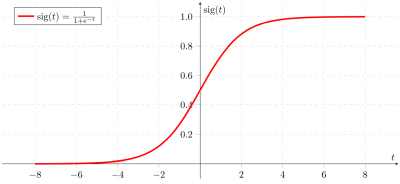
Ensuite, la plage est importante car elle nous indique les valeurs atteintes par la fonction. Une interprétation plus graphique est celle-ci: Un point \(b\) est dans la plage de \(f\) si la ligne horizontale \(y = b\) coupe le graphique de la fonction \(f(x)\).

Comment calculer le domaine, en termes pratiques?

Voici comment trouver le domaine et la plage :

Pour le domaine, vous devez d'abord trouver les points où la fonction n'est PAS définie. Les sources des opérations non définies sont la division par zéro ou la racine carrée d'un nombre négatif.

Donc, vous devez trouver les points (le cas échéant) où ces opérations non définies se produisent. Et le domaine sera le reste des points, c'est-à-dire tous les points à l'exclusion de ceux que vous trouvez qui provoquent des opérations indéfinies.

Comment calculer la gamme, en termes pratiques?

Soit \(y\) un nombre et nous résoudrons pour \(x\) l'équation suivante \(f(x) = y\). La valeur \(y\) est dans la plage si \(f(x) = y\) peut être résolue pour \(x\).

C'est donc un peu plus compliqué: vous devez trouver si vous devez restreindre \(y\) de quelque manière que ce soit afin que \(f(x) = y\) ait une solution pour \(x\).

EXEMPLE 1

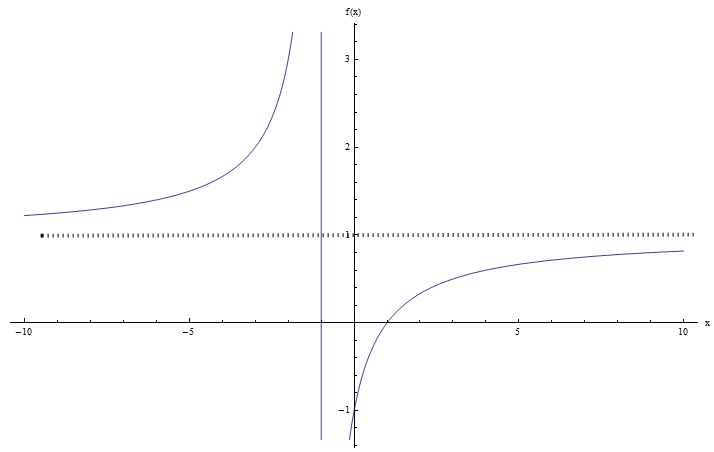
Calculez le domaine et la plage de la fonction \(\displaystyle f(x) = \frac{x+1}{x-1}\).

RÉPONDRE:

Tout d'abord, nous devons calculer le domaine. Nous devons voir où la fonction est bien fixée. Habituellement, il est plus facile de commencer là où il n'est pas bien défini.

Donc dans ce cas, toutes semblent être des opérations valides, sauf une choisie: le dénominateur ne peut pas être nul.

Remarque: La clé principale pour trouver le domaine est vérifié les points où il y a des divisions potentielles par zéro, ou des racines carrées potentielles de valeurs négatives, qui sont des opérations non valides.

Par conséquent, la fonction est bien rendue SAUF lorsque \(x-1 = 0\), ce qui se produit lorsque \(x = 1\). Par conséquent, nous disons que le domaine est la ligne réelle entière à l'exception de la valeur \(1\).

En utilisant la notation d'intervalle, nous écririons \(dom(f) = (-\infty, 1) \cup (1, +\infty)\).

Nous devons maintenant calculer la plage. En règle générale, il peut être un peu plus laborieux d'obtenir la plage que d'obtenir le domaine, mais c'est parti.

Il existe de nombreuses façons de trouver la plage: Certains peuvent s'appuyer sur la représentation graphique de la fonction pour faire une réclamation sur la plage d'une fonction. Cela pourrait fonctionner, mais ce n'est pas une vraie réponse, seulement une intuition éclairée.

L'autre manière est la manière mathématique formelle: Soit \(y\) un nombre et nous résoudrons pour \(x\) l'équation suivante \(f(x) = y\). La valeur \(y\) est dans la plage si \(f(x) = y\) peut être résolue pour \(x\).

Dans ce cas, nous avons:

Alors, quand est-ce que \(x\) est bien défini? Presque pour tous les \(y\), sauf quand \(y = 1\), car dans ce cas nous avons une division par \(0\). Par conséquent, la plage de \(f\) dans ce cas est la ligne réelle entière, à l'exception de 1.

En utilisant la notation d'intervalle, nous écririons \(R(f) = (-\infty, 1) \cup (1, +\infty)\).

EXEMPLE 2

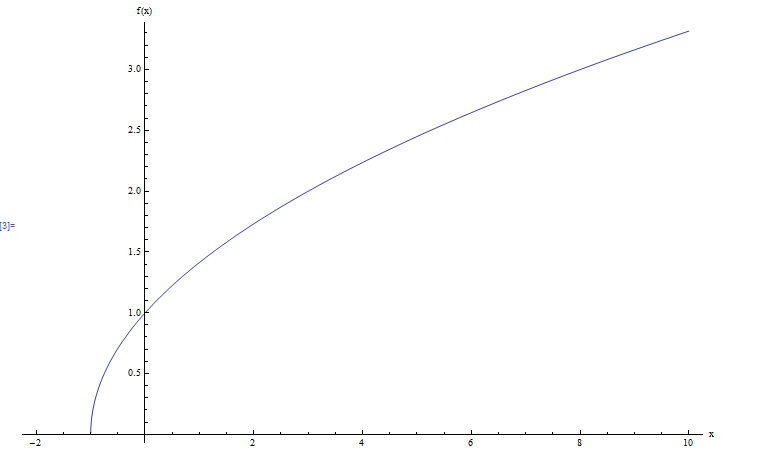
Calculez le domaine et la plage de la fonction \(\displaystyle f(x) = \sqrt{x+1}\).

RÉPONDRE:

N'oubliez pas que pour trouver le domaine, nous devons rechercher les points où des opérations non valides peuvent se produire (divisions par zéro ou racines carrées de valeurs négatives. Il n'y a pas de divisions dans ce cas, mais nous devons nous assurer que \(x+1\ge 0\) afin qu'il n'y ait pas de racines carrées Nous avons donc besoin de \(x \ge -1\). En utilisant la notation d'intervalle, nous écririons \(dom(f) = [-1, +\infty)\).

Maintenant, pour la plage, nous devons résoudre pour \(x\): \(\sqrt{x+1} = y\). La racine carrée de quelque chose n'est jamais négative, donc au moins nous avons besoin de \(y \ge 0\).

De plus, en appliquant le carré des deux côtés, nous obtenons \(x+1 = y^2\), donc la solution est \(x = y^2-1\). Donc, la seule restriction que nous devons imposer à \(y\) est que \(y \ge 0\). Par conséquent, en utilisant la notation d'intervalle, nous écririons \(R(f) = [0, +\infty)\). Graphiquement: