X-außenüberschussrechner
Anweisungen: Verwenden Sie diesen Taschenrechner, um den x-Schnur einer Linie zu ermitteln, wobei alle Schritte angezeigt werden.Zu diesem Zweck müssen Sie die Linie bereitstellen, für die Sie den X-Außenbereich benötigen.
Bitte geben Sie die Linie an, indem Sie entweder: (1) sowohl die Steigung als auch die y-Schnittstelle, (2) eine gültige lineare Gleichung (z., oder (4) zwei Punkte, an denen die Linie durchgeht.Bitte wählen Sie Ihre Wahl:
So verwenden sie diesen x-außenanscheidungsrechner mit schritten
Mit diesem Taschenrechner können Sie den x-Schnur einer Linie berechnen, und Sie erhalten alle angezeigten Schritte.
Der x-Schnittpunkt ist der Punkt, an dem die Linie die x-Achse überschreitet, wenn das jemals passiert.
Im Allgemeinen gibt es immer einen X-Schnur, wenn sich die Steigung von Null unterscheidet.
Wenn die Steigung Null ist, gibt es nur dann einen x-Schnittpunkt, wenn die Linie auch den Ursprung überschreitet.Vertikale Linien haben auch einen X-Schnittpunkt.
So finden sie x -abschnitt mit schritten mit diesem taschenrechner
Alles, was Sie tun müssen, um diesen Taschenrechner zu verwenden, ist, sich für eine der vier Optionen zur Definition Ihrer Linie zu entscheiden.Oft geben Sie den Hang und den Y-Grenzübergang an, aber Sie können auch die aufschreiben Geilung der Linie Direkt .
Wenn die von Ihnen bereitgestellte Gleichung gültig ist, wird der Löser die Schritte durchlaufen
Können sie den x-schnur aus einer linie in standardform ausnehmen?
Ja!In der Tat die Verwendung der Standardform der Linie ist eine der einfachsten Möglichkeiten, den X-Schnittpunkt zu berechnen.
Eine gemeinsame Strategie besteht also darin, zuerst die Gleichung der Linie in Standardform umzuwandeln und dann für \(x\) zu lösen, wenn \(y=0\).
Warum brauchen wir den x-schnittpunkt?
Der x-Schnur und Yabschnitt Einer Linie Nutzen Sie großartig, um eine geometrische Intuition des Verhaltens in einer Zeile in den Koordinatenachsen zu geben \(X - Y\).

Beispiel für die berechnung des x-schnur, bei dem eine linie angegeben ist
Sie kennen die Standardform der Zeile \( \frac{3}{4} x + \frac{4}{5} y = 2\).Finden Sie den X-Außenüberschuss der Linie.
Antworten:
Wir wurden mit der folgenden Gleichung versehen:
\[\displaystyle 2x+y=y+5\]Auch wen Finde du x Abfangen? : Übergeben Sie alle Variablen und ihre Koeffizienten links von der Gleichung und gruppieren die Konstanten rechts, wir bekommen:
\[\displaystyle 2x+\left(1-1\right)y = 5\]und die Vereinfachung aller Begriffe, die vereinfacht werden müssen, erhalten wir, dass die Gleichung in Standardform ist
\[\displaystyle 2x=5\]Der Begriff \( y\) erscheint nicht auf der linken Seite der Gleichung, sodass wir weiter für \( x\) lösen können, was zu
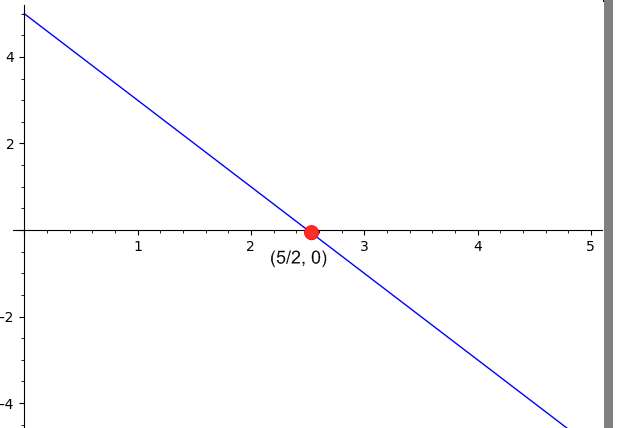
\[ 2 x = 5 \Rightarrow x=\frac{5}{2}\]Beachten Sie, dass dies basierend auf dem oben genannten entspricht einer vertikalen Linie, die über den Wert \(\displaystyle x=\frac{5}{2}\) geht.
Fazit : Basierend auf den bereitgestellten Daten schließen wir, dass die Zeile die x-Achse bei \(\displaystyle x = \frac{5}{2}\) überschreitet.





