Mehr zu diesem grafikrechner

Verwenden Sie diesen Graphikrechner, um einen Graphen einer von Ihnen angegebenen Funktion zu zeichnen. Sie können eine einfache Funktion wie f(x) = x^2 oder eine komplexere Funktion wie f(x) = tan(x)/x eingeben. Der Rechner wird versuchen, den Ausdruck zu vereinfachen, bevor er ihn grafisch darstellt.

Sobald Sie eine gültige Funktion eingegeben haben, brauchen Sie nur noch auf die Schaltfläche "Graph" zu klicken, und Sie erhalten den Graphen online, ggf. mit den entsprechenden Vereinfachungen.

Beachten Sie, dass ein gültig funktion benötigt, damit das System zweifelsfrei weiß, welche Funktion Sie grafisch darstellen wollen. Zum Beispiel ist etwas wie (sin(x))/x gültig, aber etwas wie sin x / x ist mehrdeutig, und das System wird versuchen, es auf eine Weise zu analysieren, die Sie vielleicht nicht beabsichtigt haben.

Wie geht man bei der grafischen darstellung von funktionen vor?

Die Erstellung von Diagrammen kann sehr einfach sein, wenn die Funktionen einfach sind. Es geht nur darum, die Paare (x, y) = (x, f(x)) zu identifizieren und den passenden Fensterrahmen zu finden, um sie darzustellen.

Diese Graphing Calculator online erleichtert Ihnen die Entscheidung, welche Punkte Sie grafisch darstellen wollen, und die Wahl des richtigen Fensters für die Anzeige.

Schritte zur grafischen darstellung einer funktion

• Schritt 1: Bestimmen Sie eindeutig die Funktion, die Sie darstellen wollen, und führen Sie alle offensichtlichen Vereinfachungen durch. Wenn die Funktion zum Beispiel irgendwo \(\sin^2(x) + \cos^2(x)\) enthält, müssen Sie feststellen, dass \(\sin^2(x) + \cos^2(x) = 1\) und dann Vereinfachen das in Ihrem Ausdruck.
• Schritt 2: Nachdem alle offensichtlichen Vereinfachungen vorgenommen wurden, müssen Sie einen Bereich für die x-Werte festlegen. Hierfür gibt es keine festen Regeln, aber in der Regel müssen Sie alle relevanten Punkte berücksichtigen, wie Unstetigkeiten, vertikale Asymptoten usw.
• Schritt 3: Sobald der Bereich der X-Werte festgelegt ist, müssen Sie sich eine Vorstellung von dem Bereich der Y-Werte machen, damit kein Punkt des Diagramms außerhalb des Rahmens liegt.

Die Idee der Erstellung von Diagrammen ist also einfach, aber Sie müssen immer noch ein paar Dinge entscheiden, wenn Sie die Dinge manuell tun würden. Die Verwendung eines Diagramm-Tools wird definitiv jedes Rätselraten beseitigen.

Warum muss ich eine funktion grafisch darstellen?

Das Diagramm, das Ihnen dieser Online-Grafikrechner zur Verfügung stellt, stellt sicher, dass Sie eine wirklich gute Darstellung des Verhaltens der Funktion erhalten. Kreuzt sie die x- oder y-Achse, hat sie lokale Höchst- oder Tiefstwerte? Sie können eine Menge relevanter Informationen über die Funktion erhalten, wenn Sie sich nur den Graphen ansehen.

Sie werden nicht unbedingt die genauen Schnittpunkte oder Extrema kennen, wenn Sie sich das Diagramm ansehen, aber Sie werden eine ziemlich gute Vorstellung davon haben, wo sie zu finden sind, falls sie überhaupt existieren.

Vorteile der verwendung eines diagrammwerkzeugs

Wie gesagt, es ist nicht allzu schwierig, ein Diagramm zu erstellen, aber es gibt einige Details, die geregelt werden müssen, insbesondere die, die den Fensterrahmen bestimmen, der angezeigt werden soll.

Das bedeutet, dass Sie ein "richtiges" Diagramm für eine Funktion haben können, das aber einen Teil des Diagramms anzeigt, der nicht so wichtig ist, und Sie können die meisten wichtigen Teile der Funktion auslassen, die angezeigt werden sollten. Ein guter Graphenersteller übernimmt diese Aufgabe für Sie.

Beispiel: berechnung des graphen einer funktion

Finden Sie den Graphen der Funktion: \(f(x) = \displaystyle \frac{\sin x}{x}\)

Lösung: Die folgende Funktion wurde bereitgestellt: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), für die wir ihren Graphen konstruieren müssen.

Beachten Sie, dass die Funktion bei \(x = 0\) nicht definiert ist, obwohl sie eine reparable Unstetigkeit aufweist, da

\[\lim_{x\to 0} \frac{\sin x}{x} = 1\]

Die folgende Darstellung ergibt sich für die gegebene Funktion auf dem Intervall \([-5, 5]\):

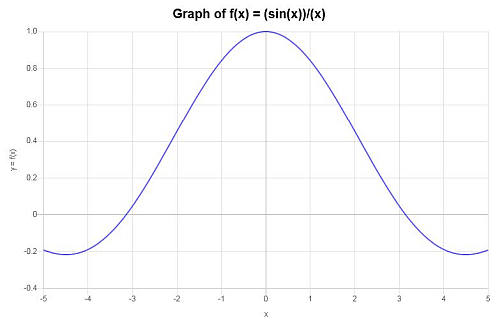
womit die Berechnung abgeschlossen ist.

Mehr grafische rechner online

Obwohl diese Graph Maker in dem Sinne generisch ist, dass es jede Art von Funktion darstellen kann, können Sie auch einige spezialisierte Arten von Graphen für bestimmte Funktionen verwenden, die Ihnen mehr Informationen auf der Grundlage der Struktur der Funktion geben können.

Sie können zum Beispiel verwenden liniengrafik-Rechner das speziell für die grafische Darstellung von Linien konzipiert ist. Wenn Sie mit trigonometrischen Funktionen arbeiten, können Sie Folgendes verwenden Trigendrecht das auch versucht, spezifische Parameter von trigonometrischen Funktionen zu finden, einschließlich Amplitude, Periode, Frequenz, usw.

Oder Sie können Folgendes verwenden Polynomdiagramm wenn es um Polynome geht.

Sie können auch Folgendes verwenden Exponentialfunktion -Wiederaufnahme um die Parameter einer Exponentialfunktion zu bestimmen, wenn zwei Punkte gegeben sind, durch die die Kurve verläuft.