Nichtparametrische Statistiken oder was zu tun ist, wenn die Annahmen für einen parametrischen Test fehlschlagen

Der Mittelwert, der Median und der Modus sind die häufigsten Maße für die zentrale Tendenz, mit denen das Zentrum einer Verteilung beschrieben wird. Von den dreien ist der Mittelwert der am häufigsten verwendete, aber auch der Median und der Modus sind weit verbreitet.

Wir müssen unterscheiden zwischen dem Stichprobe Mittelwert, Median und Modus und deren Population Gegenstücke.

Normalerweise sind wir es mit einer Probe versehen und wir müssen den Stichprobenmittelwert, den Stichprobenmedian und den Stichprobenmodus berechnen. Diese Statistiken sind Schätzer der entsprechenden Populationsparameter.

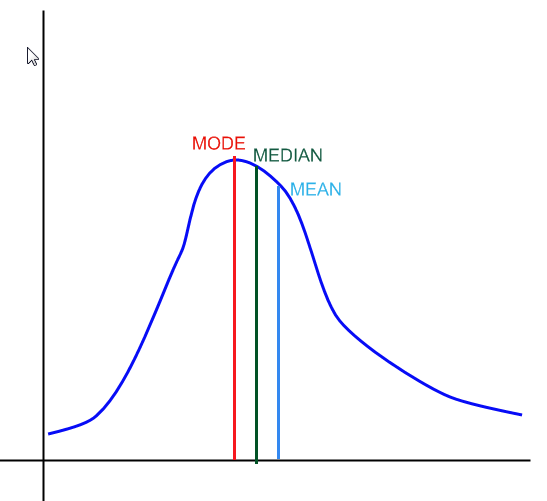
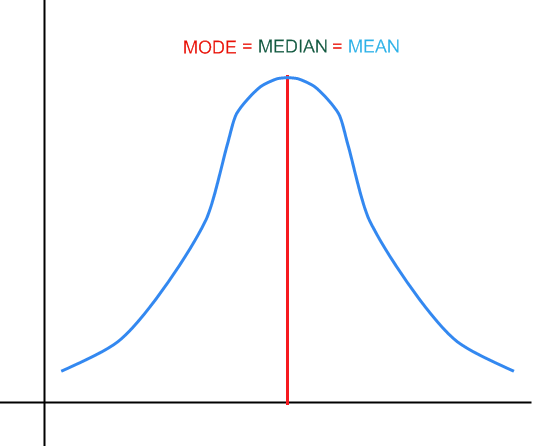
In der obigen Grafik sehen Sie ein Beispiel dafür, wie der Median, der Modus und der Mittelwert in einer Verteilung aussehen würden.

Der Modus entspricht dem am häufigsten wiederholten Wert in einer Probe. In einer Verteilung entspricht dies dem höchsten Punkt in der Dichtefunktion, wie in der obigen Grafik gezeigt.

Der Median definiert ungefähr den Punkt, an dem 50% der Verteilung links davon und rechts davon liegen.

Der Mittelwert entspricht dem gewichteten Durchschnitt der Werte, die die Variable annimmt, und den zugehörigen Wahrscheinlichkeiten (\(\sum x \cdot p(x)\)). Für eine Verteilung ist eine solche gewichtete Summe entweder eine Summe oder ein Integral. Für eine Stichprobe berechnen wir einfach den Durchschnitt der Werte in der Stichprobe.

Berechnen des Mittelwerts, des Medians und des Modus für eine bestimmte Stichprobe

Nehmen wir nun an, wir erhalten eine Stichprobe \(X_1, X_2, ..., X_n\) und möchten den Modus, den Median und den Mittelwert berechnen. Wie gehen wir vor?

• • Für den Modus: Einfach. Wir finden nur die Nummer, die am häufigsten wiederholt wird. Beispiel: Wenn wir eine Stichprobe 1, 2, 2, 2, 3, 1, 4 haben, ist der Modus 2, da 2 der am häufigsten wiederholte Wert ist (er wird dreimal wiederholt).

• • Für den Median: Diese Berechnung ist etwas komplizierter. Nehmen Sie Ihre Probe \(X_1, X_2, ..., X_n\) und der erste Schritt besteht darin, sie in aufsteigender Reihenfolge neu zu organisieren. Nehmen Sie also an, dass \(\hat X_1, \hat X_2, ..., \hat X_n\) das Beispiel ist, nachdem Sie es vom niedrigsten zum höchsten Wert neu angeordnet haben.

Nun werden wir die Position des Medians in der Stichprobe in aufsteigender Reihenfolge berechnen. Für die Stichprobengröße \(n\) berechnen wir \(P = 0.5 (n+1)\).

Wenn dieser Wert eine ganze Zahl ist, stellen wir fest, dass der Median der Wert in P ist ^th Position in der Probe in aufsteigender Reihenfolge.

Wenn dieser Wert KEINE Ganzzahl ist, finden wir \(P_L\) und \(P_U\), die die nächsten Ganzzahlen links und rechts von \(P\) sind. (Beispiel: Wenn \(P = 10.2\), dann \(P_L = 10\) und \(P_U = 11\)).

Der Median ist dann der Durchschnitt der Werte und der Einstellungen \(P_L\) ^th und \(P_U\) ^th in der Versammlung in aufsteigender Weise. Keine Sorge, wir werden sterben eines Beispiels versucht.

• • Für den Interessen: Einfach auch. Der Teilmittelwert wird nach der Formel geändert

\[\displaystyle \frac{1}{n}\sum_{i=1}^n X_i\]

BEISPIEL 1

Finden Sie die den, den Median und den Modus für das Lesen Beispiel:

28, 36, 43, 30, 15, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 12, 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51

ANTWORTEN:

Die vollständige Tabelle zeigt die Möglichkeit, die Rechte des Urteils zu überprüfen

	Daten
	28
	36
	43
	30
	Teile
	19
	46
	36
	34
	38
	42
	29
	37
	35
	39
	39
	30
	39
	36
	38
	30
	41
	42
	46
	40
	33
	30
	40
	43
	12
	42
	39
	30
	35
	38
	41
	30
	37
	40
	30
	30
	35
	39
	37
	42
	42
	37
	38
	32
	51

Summe =	1791
Ursachen =	35,82

Der Versatzmittelwert ist dafür

\[\bar{X}=\frac{1}{n}\sum{{{X}_{i}}}=\frac{1791}{50}=35.82\]

Für den Median zeigt die folgenden Tabelle die Daten in aufsteigender Weise:

Daten
12
Teile
19
28
29
30
30
30
30
30
30
30
30
32
33
34
35
35
35
36
36
36
37
37
37
37
38
38
38
38
39
39
39
39
39
40
40
40
41
41
42
42
42
42
42
43
43
46
46
51

In diesem Fall ist die Position des Medians P = 0,5 * (50 + 1) = 25,5, auch \({{P}_{L}}=25\) und \({{P}_{U}}=26\). Der Wert in Position 25 ^th in den Daten in aufsteigender Anzahl ist 37, und der Wert in Position 26 ist auch 37. Der Median ist dann

\[Median=\frac{{37}+{37}}{2}=37\]

Der Modus ist der 30.

War es der Grund, der Verlust, der Median oder der Modus?

Das ist eine Frage. Im Allgemeinen gibt es nicht für alle Distributionen eine Antwort. Das heißt, die Antwort gehört von der Verteilung ab.

Für eine symmetrische Verteilung haben wir :: ::

\[\Large \text{Mode} = \text{Median} = \text{Mean} \]

Grafisch:

Mittelwert, Median und Modus für eine symmetrische Verteilung

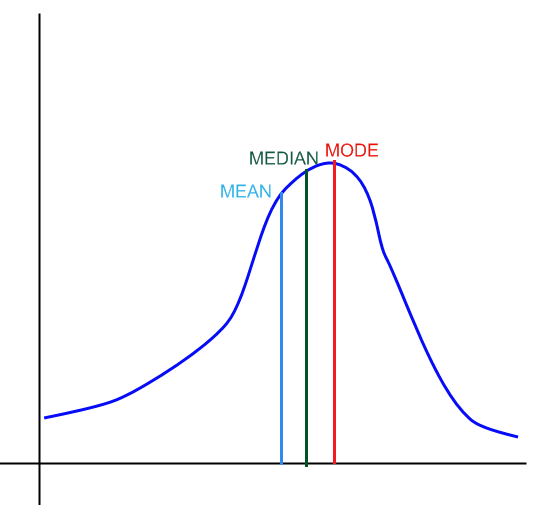
Für eine rechtwinklige Verteilung haben wir :: ::

\[\Large \text{Mode} \le \text{Median} \le \text{Mean} \]

Grafisch:

Für eine linksgerichtliche Verteilung haben wir :: ::

\[\Large \text{Mean} \le \text{Median} \le \text{Mode} \]

Grafisch:

Median, Mittelwert und Modus für eine linksgerichtete Verteilung

Mehr über Eigenschaften, Median und Modus

Der Median, der Verlust und der Modus sind weitreichende Kenntnisse, die Rechte in der Statistik werden. Sie stellen Mittelmaße dar, die versuchen, einen für die öffentlichen Regierungsativen Wert zu erhalten.

Verschiedenig vom Maß.

• Für Nenndaten werden wir den Modus.

• Für ordinale, nicht quantitative Daten verwenden wir den Modus und das Maß für die Mitte.

• Für ordinale, quantitative Daten verwenden wir den den Median oder den Wert als Maß für die Mitte.

• Für Intervall- und Verhältnisdaten werden als Maß für die Mitte verwendet.

Anwendungen

Der Verlust, der Median und der Modus sind die gleichen Rechte für die Mitte. Der Wert und der Median werden für quantitative Daten verwendet, und der Modus wird für kategoriale Daten verwendet.

Für quantitative Daten, die sich auf den Verlust beziehen. Mit einer Verantwortung: Der Kontakt ist sehr wahrnehmbar Ausreißern. Dies bedeutet, dass ein Ausreißer den Wert des Mittelwerts drastisch verändert kann.

In wahrheitsmäßig, wenn es Ausreißer gibt oder die Teilung verzerrt ist, ist es vorzuziehen, den Median als genauestes Maß für die Mitte zu verwenden, da der Verlust durch Schiefe oder Ausreißer verzerrt wird.

Ein Beispiel hierfür ist die Entnahme von Prüfung zur Beurteilung des Einkommens der Wahrnehmung. Wenn wir eine Person von 100 Personen übernehmen und unterscheiden, dass 99 von ihnen 10.000 USD pro Jahr und 1 Person 100 Millionen USD pro Jahr verdienen, die das Eigentum von diesen 10.000 (99 * 1 + 100.000.000) / 100 = 1,009 900,00 USD. Im ersten Teil jedes 1.009.900,00 USD, gehört Sie auf die Idee kommen, dass diese sich aus einem sehr persönlichen Gebiet unterscheiden, aber das ist nicht der Fall: Es ist nur ein Ausreißer, der den starken stark verzerrt. In diesem Fall wurde der Median von 10.000 USD für diesen Kontakt einen viel repräsentativeren Wert des zentralen Inhalts.