Gaußsche Eliminierung
Die Gaußsche Eliminierung ist ein Prozess, der an Matrizen durchgeführt wird, in die eine Matrix eingefügt werden soll Staffelform . Eine Matrix in einer solchen Form zu haben, hilft enorm, Matrixgleichungen sehr einfach zu lösen.
Technisch gesehen besteht der Prozess der Durchführung der Gaußschen Eliminierung darin, eine Spalte mit einem Drehpunkt zu finden (was der ausgefallene Slang für ein Nicht-Null-Element ist), mit dem wir alle Elemente unterhalb des Drehpunkts entfernen können.
Dieser Prozess des Findens und Eliminierens von Drehpunkten ermöglicht es uns, eine Matrix in Staffelform zu bringen. Der Prozess ist so, dass Sie durch Drehen eine neue Spalte zur Staffelform hinzufügen und die Staffelform, die Sie haben, nicht „ruinieren“ habe den vorherigen Schritt wieder gut gemacht. Schön, wenn du mich fragst.
Der Begriff "Staffelform", der unter Verwendung der Gaußschen Eliminierung erhalten wird, wird durch Betrachten der obigen Matrix deutlich, in der die Nicht-Null-Elemente der Matrix diese echelonenartige Struktur aufweisen, wie durch die rote Linie gezeigt.
Die Mathematik hinter dem Schwenken und der Gaußschen Eliminierung
Wir werden nicht zu technisch darauf eingehen, wir werden nur versuchen, dass Sie die Motivation und die Mechanik dieser Art der Eliminierung verstehen.
Die Idee ist, eine Matrix \(A\) mit der Dimension \(m \times n\) (dh mit \(m\) Zeilen und \(n\) Spalten) in eine andere Form zu bringen, die für das Lösen von Gleichungen besser geeignet ist.
Insbesondere müssen wir für eine \(m\times n\) Matrix \(A\) und einen \(m\times 1\) Vektor \(b\) einen \(n\times 1\) Vektor \(x\) finden, so dass
\[Ax = b\]Sie denken vielleicht, "das ist so einfach, wir multiplizieren einfach jede Seite mit \(A^{-1}\) von links", damit wir Folgendes erhalten:
\[x = A^{-1} b \]....Nicht so schnell! Das funktioniert nur, wenn die Matrix \(A\) invertierbar ist. Zu Beginn muss die Matrix \(A\) eine quadratische Matrix sein, und dann muss sich ihre Determinante von Null unterscheiden. Sie können jedoch nicht mit der Umkehrung für nicht quadratische Matrizen multiplizieren. Also, wie machst du das dann?
Sie müssen die Gleichung in eine Gleichung umwandeln, die einfacher zu lösen ist.
Insbesondere sind Matrizen in Staffelform Matrizen, die zu Gleichungen führen, die leicht zu lösen sind (dazu später mehr).
Elementarmatrizen verwenden
Zunächst werden wir eine wichtige Anmerkung machen. Wenn wir eine Lösung der Matrixgleichung \(Ax = b\) haben und \(E\) eine invertierbare Matrix ist, dann ist \(x\) auch eine Lösung von \((EA)x = Eb\) und umgekehrt.
Mit anderen Worten, die Matrixgleichungen
\[Ax = b\]und
\[(EA)x = Eb\]sind äquivalent für eine invertierbare Matrix \(E\). Was meinen wir damit, dass die Gleichungen äquivalent sind? Wir meinen, dass die Gleichungen die gleichen Lösungen haben.
Wir beginnen also mit \(Ax = b\) und kommen durch Multiplikation mit invertierbaren Matrizen \(E\) zu einer äquivalenten Matrixgleichung viel einfacher zu lösen .
Angenommen, wir können eine Liste invertierbarer Matrizen \(E_1, E_2, ..., E_n\) finden und multiplizieren (von links) die ursprüngliche Matrixgleichung, um sie in eine äquivalente Gleichung umzuwandeln, wie:
\[Ax = b \,\,\,\, \Leftrightarrow \,\,\,\, (E_1 \cdot A)x = (E_1 \cdot b)\] \[... \Leftrightarrow \,\,\,\, (E_n \cdots E_2 \cdot E_1 \cdot A)x = (E_n \cdots E_2 \cdot E_1 \cdot b)\] \[ \Leftrightarrow \,\,\,\, \tilde A x = \tilde b\]wo \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) und \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\).
Unser Ziel ist es, sorgfältig wählen die invertierbaren Matrizen \(E_1, E_2, ..., E_n\), so dass \(\tilde A\) in Staffelform vorliegt.
Warum ist das so? Denn wenn \(\tilde A\) in Staffelform vorliegt, ist das Lösen der Matrixgleichung \(\tilde A x = \tilde b\) viel einfacher, und wir wissen bereits, dass \(\tilde A x = \tilde b\) die gleichen Lösungen wie \(A x = b\) hat
BEISPIEL 1
Lassen Sie uns sehen, warum das Lösen einer Matrixgleichung viel einfacher ist, wenn Sie sie in Staffelform haben. Stellen Sie sich zunächst vor, Sie haben die folgende Matrix und den folgenden Vektor:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & -1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]und Sie möchten \(Ax = b\) lösen. Wie würde das Gleichungssystem aussehen? Das System \(Ax = b\) würde so aussehen
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 - x_3 = 1\]Wie sieht es aus? Na ja, nicht so ordentlich. Sie müssten anfangen, Gleichungen zu jonglieren. Es gibt mehr oder weniger systematische Ansätze, um dies mit Dingen wie Eliminierung und dergleichen zu lösen, aber es ist zumindest umständlich.
Stellen Sie sich andererseits vor, Sie haben die folgende Matrix und den folgenden Vektor:
\[\tilde A = \left[ \begin{matrix} -1 & 1 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{matrix} \right] \] \[\tilde b= \left[ \begin{matrix} 1 \\ -1 \\ -1 \\ \end{matrix} \right]\]und Sie möchten \(\tilde A x = \tilde b\) lösen. In diesem Fall liegt die Matrix \(\tilde A\) in Staffelform vor. Wie würde das Gleichungssystem aussehen? Das System \(\tilde A x = \tilde b\) würde so aussehen
\[-x_1 + x_2 + x_3 = 1\] \[x_2 - x_3 = -1\] \[x_3 = -1\]Wie sieht dieser aus? Na ja, nicht zu schäbig.
Wenn wir direkt von der dritten Gleichung ausgehen, haben wir tatsächlich \(x_3 = -1\) direkt. Dann aus der zweiten Gleichung \(x_2 = -1 + x_3 = -1 + (-1) = -2\). Und ab der ersten Gleichung \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\). Ohne Flaum haben wir also Folgendes gefunden:
\[x_1 = -4, \, x_2 = -2, x_3 = -1\]Daher ist das System in diesem Fall trivial gelöst.
Für Systeme, die Matrizen in Staffelform zugeordnet sind, ist es einfach, von der letzten Gleichung zur ersten Gleichung zurückzukehren, um die Lösungen zu erhalten.
So wählen Sie die richtigen invertierbaren Matrizen aus
Jetzt, da wir wissen, dass das Arbeiten mit Matrizen in Staffelform das Lösen von Matrixgleichungen sehr viel einfacher macht, sollten wir uns fragen, welche invertierbaren Matrizen \(E_1, E_2, ..., E_n\) \(\tilde A\) in Staffelform ergeben.
Wie funktioniert die Gaußsche Eliminierung?
Interessanterweise ist es nicht schwer, diese Matrizen \(E_1, E_2, ..., E_n\) zu finden, die als Elementarmatrizen bezeichnet werden.
Schritt 1
: Sehen Sie sich die erste Spalte an. Wenn sie einen Wert ungleich Null hat, ist dies Ihr Dreh- und Angelpunkt. Wenn die erste Zeile der ersten Spalte nicht Null ist, verwenden Sie sie als Drehpunkt. Wenn nicht, suchen Sie eine Zeile mit einem Wert ungleich Null und permutieren Sie diese Zeile und die erste Zeile.
Sie finden also einen Drehpunkt und müssen möglicherweise eine Zeilenpermutation durchführen (die tatsächlich durch Multiplikation mit einer bestimmten invertierbaren Matrix dargestellt wird).
Schritt 2
: Wenn Sie einen Drehpunkt haben, entfernen Sie alle Elemente in der aktuellen Spalte unterhalb des Drehpunkts.
Dazu wird die Pivot-Zeile mit einer bestimmten Konstante multipliziert und zu einer Zeile unterhalb des Pivots addiert, sodass das Element in derselben Spalte wie der Pivot auf Null gesetzt wird.
Schritt 3
: Wenn alle Elemente unter dem Drehpunkt durch geeignete Zeilenoperationen (die zufällig durch die Operation einer invertierbaren Matrix dargestellt werden) auf Null gesetzt wurden, wechseln Sie zur nächsten Spalte, zur nächsten Zeile und suchen Sie nach einem Drehpunkt aus der unteren Zeile der Reihe des vorherigen Drehpunkts und machen Sie das gleiche Verfahren.
Schritt 4
: Wiederholen Sie diesen Vorgang, bis Ihnen die Spalten ausgehen oder die Matrix in Staffelform vorliegt.
BEISPIEL 2
Lösen Sie das folgende System mithilfe von Schwenken und Gaußscher Eliminierung:
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 + x_3 = 1\]ANTWORTEN:
Zunächst sind die zugehörige Matrix \(A\) und der Vektor \(b\):
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]Die erweiterte Matrix \([A|b]\) ist
\[\left[ \begin{matrix} 1 & 1 & 1 & 2 \\ 1 & -1 & 1 & 1 \\ -1 & 1 & 1 & 1 \\ \end{matrix} \right]\]Um das System zu lösen, müssen wir die Gaußsche Eliminierung durchführen. Wir wählen den ersten Drehpunkt, beginnend mit der ersten Spalte. Das Element in der ersten Zeile der ersten Spalte ist 1, was sich von Null unterscheidet, und wird dann als Drehpunkt verwendet. Wir verwenden diesen Drehpunkt (1), um alle Elemente darunter zu entfernen:
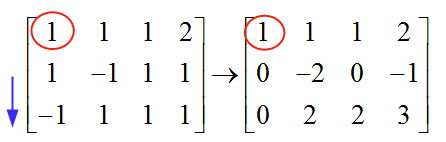
Die Mechanik zum Entfernen der Elemente unterhalb des Drehpunkts ist einfach. In diesem Fall subtrahiere ich die Elemente in Zeile 1 von den Elementen in Zeile 2, um die "1" zu eliminieren, die sich unter dem Drehpunkt befindet. Auf diese Weise bilde ich eine Null unter dem Drehpunkt.
Um das "-1" in Zeile 3 zu entfernen, füge ich die Elemente in Zeile 1 zu den Elementen in Zeile 3 hinzu. Auf diese Weise bilde ich eine Null unter dem Drehpunkt in Zeile 3.
Wir werden sehen, dass diese Zeilenoperationen durch Multiplikation mit der invertierbaren Matrix erreicht werden, sodass wir auf diese Weise äquivalente Systeme haben.
Wenn wir nun zur nächsten Zeile, zur nächsten Spalte übergehen, finden wir ein "-2", das sich von Null unterscheidet, und daher wird es als unser Drehpunkt verwendet. Um den Wert unterhalb dieses Pivots zu eliminieren, fügen wir Zeile 3 die Werte von Zeile 2 hinzu:
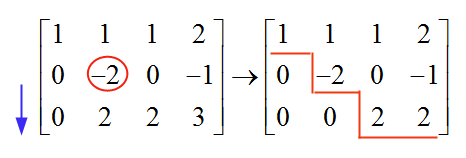
und jetzt hören wir auf, weil die resultierende Matrix bereits in Staffelform vorliegt. Jetzt gehen wir zurück, um das System zu lösen:
\[2x_3 = 2 \,\,\,\, \Rightarrow \,\,\,\, x_3 = 1\] \[-2x_2 = -1 \,\,\,\, \Rightarrow \,\,\,\, x_2 = 1/2\] \[x_1+x_2+x_3 = 1 \,\,\,\, \Rightarrow \,\,\,\, x_1 = 1 - x_2 - x_3 = 1 - 1/2 - 1 = -1/2\]Weitere Informationen zur Gaußschen Eliminierung
Das Schwenken und Verwenden der Schwenkeliminierung sind die Grundpfeiler für die Lösung linearer Systeme. Aber es geht darüber hinaus. Wenn wir uns nur um lineare Systeme kümmern würden, würden wir verwenden Cramers Regel , was gut funktioniert für Lösungssysteme .
Die Gaußsche Eliminierung hat den Vorteil, dass sie eine systematische Methode zum Einfügen von Matrizen in Reihenebenen bietet, was wiederum zum schnellen Erhalten bestimmter Matrixzerlegungen (LU, LDU usw.) oder sogar zur Berechnung der Inversen der Matrix führt .
Elementare Permutationsmatrizen
Es gibt keine allgemeinen Regeln, um allgemeine Ausdrücke zu berücksichtigen. Wir müssen nach Gehör spielen und versuchen, die Struktur des Ausdrucks auszunutzen. Manchmal können wir faktorisieren, manchmal nicht. Es hängt alles vom Ausdruck ab. Die einzige allgemeine Regel besteht darin, zu versuchen, gemeinsame Faktoren zu gruppieren und zu finden, um sie weiter zu gruppieren und zu vereinfachen.
Elementarmatrizen von Zeilenoperationen
Der Schlüssel der Pivot-Methode zum Finden von Lösungen besteht darin, dass die Permutationen und Zeilenoperationen invertierbare Matrizen sind, sodass das System, das wir bei jedem Schritt transformieren, dem ursprünglichen System entspricht.
In der Tat werden sowohl die Permutation von Zeilen als auch Zeilenoperationen durch invertierbare Matrizen dargestellt. Betrachten Sie die Matrix \(E_{ij}\), die erhalten wird, indem Sie die Identitätsmatrix \(I\) nehmen und ihre Zeilen \(i\) und \(j\) permutieren.
Durch Multiplizieren der Matrix \(E_{ij}\) mit einer beliebigen Matrix \(A\) von links werden die Zeilen \(i\) und \(j\) von \(A\) permutiert.
Betrachten Sie nun die Matrix \(E_{ij}^{\lambda}\) für \(i < j\), die der Identitätsmatrix für alle Zeilen entspricht, mit Ausnahme der Zeile \(i\), in der der Wert von i angegeben ist th Spalte ist \(\lambda\) anstelle von 0.
Wie wäre es mit den Operationen mit Spalten?
Manchmal müssen wir Spalten permutieren, um einen Drehpunkt zu finden. In diesem Fall müssen wir die Matrix \(E_{ij}\) von RECHTS multiplizieren, und das Ergebnis ist, dass die Spalten \(i\) und \(j\) von \(A\) permutiert werden.