Absolutwert-Ungleichungen
Absolutwert-Ungleichungen sind Ungleichungen, bei denen es eine oder mehrere gibt absoluter Wert . Erinnern wir uns, dass eine Ungleichung fast wie eine Gleichung ist, aber anstelle des Zeichens "=" haben wir "≤" oder "≥".
Dieser Unterschied macht es so, dass der Lösungssatz typischerweise eine Region ist, wie bei den meisten Ungleichungen. Und die Tatsache, dass es sich um absolute Werte handelt, deutet auf eine besondere Behandlung ihrer Auflösung hin.
In diesem Tutorial konzentrieren wir uns auf die spezifischen Fähigkeiten, die für die Lösung dieser Art von Ungleichung erforderlich sind, die einen oder mehrere absolute Werte enthält. Wir gehen auch davon aus, dass eine oder zwei Variablen, \(x\) und / oder \(y\), an der Ungleichung beteiligt sind.
Was ist eine absolute Wertungleichheit?
Für die Zwecke dieser Analyse betrachten wir eine Absolutwertungleichung als eine Ungleichung mit einer oder zwei Variablen mit mindestens einem Absolutwert.
Im Folgenden haben wir beispielsweise eine Absolutwertungleichung mit zwei Variablen \(x\) und \(y\):
\[|3x+2y-1| \ge 1\]Oder wir könnten die folgende absolute Ungleichung mit nur einer Variablen haben:
\[|3x-1| \le 2\]Für unsere Zwecke und für die Zwecke der Techniken, die für ihre Auflösung verwendet werden, werden wir uns mit beiden Arten von Ungleichungen befassen (eine und zwei Variablen).
Wie löse ich absolute Ungleichungen?
Beim Lösen von Gleichungen oder Ungleichungen gibt es nicht wirklich eine Silberkugel, die alles löst. Jedes Problem ist anders und kann seine eigenen Besonderheiten haben.
Das Beste, was wir tun können, ist, eine Reihe von Schritten bereitzustellen, die Sie bei der Lösung einer Ungleichung unterstützen.
Schritt 1:
Bestimmen Sie für jedes Absolut die Regionen, in denen das Argument des Absolutwerts negativ und in denen es nicht negativ ist.
Schritt 2:
Wenn die Ungleichung nur einen absoluten Wert enthält, lösen Sie ihn in beiden Bereichen (wobei das Argument des absoluten Werts negativ und nicht negativ ist).
Schritt 3:
Wenn die Ungleichung mehr als einen absoluten Wert enthält, müssen Sie alle Regionen schneiden, um eine Reihe kleinerer Partitionen zu erhalten. In jeder Partition müssen Sie genau das Vorzeichen jedes Arguments kennen. Lösen Sie dann die Ungleichung in allen Bereichen.
Schritt 4:
Sobald Sie die Teilelösung erhalten haben, die sich in jedem der Bereiche befindet, ist die endgültige Lösung einfach die Vereinigung dieser Teilelösungen.
Mit einfachen Worten: Sie müssen die Regionen herausfinden, in denen Sie das Vorzeichen des Arguments der absoluten Werte genau kennen (damit Sie sie entfernen können).
Einige Beispiele sollen diese Schritte verdeutlichen.
BEISPIEL 1
Lösen Sie die folgende Ungleichung
\[| 2x + 4y - 1 | \ge 2\]ANTWORTEN:
Um die Ungleichung zu lösen, müssen wir die oben angegebenen Schritte ausführen.
Schritt 1: Es gibt nur einen absoluten Wert, daher müssen wir feststellen, ob das Argument negativ und nicht negativ ist. Deshalb müssen wir zuerst lösen:
\[2x + 4y - 1 \ge 0\]Es gibt verschiedene Strategien, um das Obige zu lösen, aber die einfachste besteht darin, zuerst die Gleichung zu lösen
\[2x + 4y - 1 = 0\]Dies bedeutet, dass \(4y = -2x + 1\) oder dasselbe wie \(y = -\frac{1}{2}x + \frac{1}{4}\), was einer Linie mit Steigung \(m = -\frac{1}{2}\) und y-Achsenabschnitt \(n = \frac{1}{4}\) entspricht.
Um uns nun um \(2x + 4y - 1 \ge 0\) zu kümmern, testen wir, ob der Punkt \((0,0)\) die Ungleichung erfüllt oder nicht:
\[2(0) + 4(0) - 1 = -1 < 0\]\((0,0)\) erfüllt also die Ungleichung oder nicht. Die Schlussfolgerung ist, dass die Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = \frac{1}{4}\) die Ebene in zwei Regionen unterteilt:
Für die Punkte unterhalb der Linie (wir nennen diese Region 1 \(R_1\)) erhalten wir \(2x + 4y - 1 < 0\)
Für die Punkte über der Linie, einschließlich der Linie selbst (wir nennen diese Region 2 \(R_2\)), erhalten wir \(2x + 4y - 1 \ge 0\)
Warum ist das wichtig? Warum nehmen wir uns all diese Mühe? Denn auf \(R_1\) erhalten wir das seit \( 2x + 4y - 1 < 0\), dann \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). In ähnlicher Weise erhalten wir auf \(R_2\) das seit \( 2x + 4y - 1 \ge 0\), dann \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Schritt 2: Jetzt müssen wir die Ungleichung in Region 1, \(R_1\), lösen ::
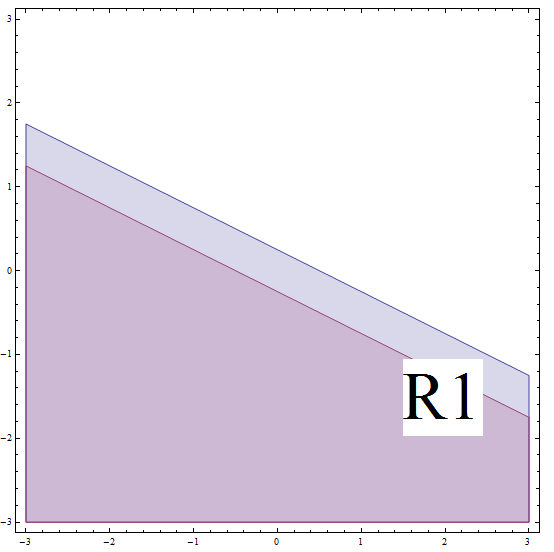
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]Dies entspricht allen Punkten unterhalb oder auf der Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = -\frac{1}{4}\). Vergessen Sie jedoch nicht, dass Sie sich auf \(R_1\) befinden. Diese gefundene Zeile befindet sich UNTER der Grenze von \(R_1\) (siehe Grafik unten).
Da wir davon ausgehen, dass wir uns in \(R_1\) befinden, müssen wir zur Verdeutlichung haben, dass wir UNTER der Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = \frac{1}{4}\) sind. Unter dieser Annahme haben wir die ursprüngliche Ungleichung gelöst und müssen auch unter der Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = -\frac{1}{4}\) liegen. Diese beiden Bedingungen müssen gleichzeitig auftreten, damit wir den Schnittpunkt der beiden Regionen erhalten.
Die Teillösung entspricht in diesem Fall also allen Punkten unterhalb oder auf der Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = -\frac{1}{4}\).
Jetzt müssen wir die Ungleichung in Region 2, \(R_2\), lösen ::
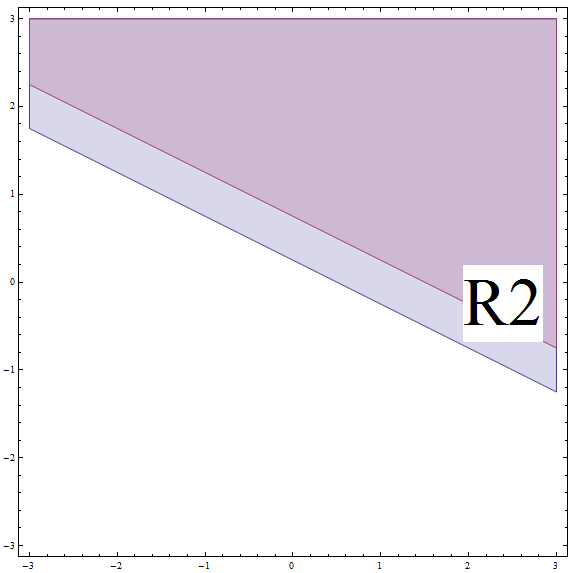
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]Dies entspricht allen Punkten über oder auf der Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = \frac{3}{4}\). Vergessen Sie jedoch nicht, dass Sie sich auf \(R_2\) befinden und diese Linie über der Grenze von\(R_2\) liegt (siehe Grafik unten).
Wenn wir den Schnittpunkt zwischen \(R_2\) und dem darüber liegenden Bereich finden, erhalten wir, dass die Teillösung in diesem Fall alle Punkte über oder auf der Linie mit der Steigung \(m = -\frac{1}{2}\) und dem y-Achsenabschnitt \(n = \frac{3}{4}\) sind.
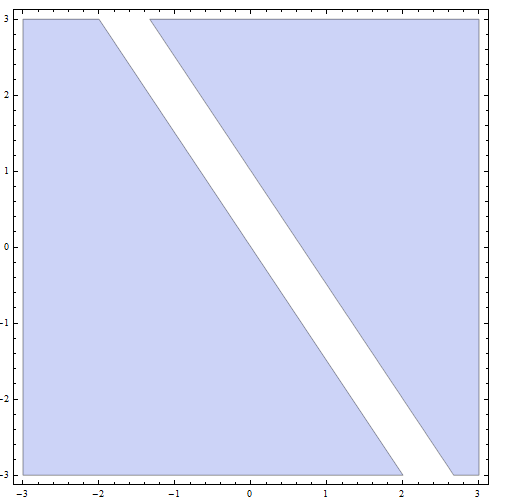
Schritt 4: Die endgültige Lösung ist nun die Vereinigung aller Teillösungen aus den vorherigen Teilen: Die endgültige Lösung sind alle Punkte UNTEN oder auf der Linie mit Steigung \(m = -\frac{1}{2}\) und y-Achsenabschnitt \(n = -\frac{1}{4}\), PLUS alle Punkte OBEN oder auf der Linie mit Steigung \(m = -\frac{1}{2}\) und y-Achsenabschnitt \(n = \frac{3}{4}\).
Grafisch bekommen wir
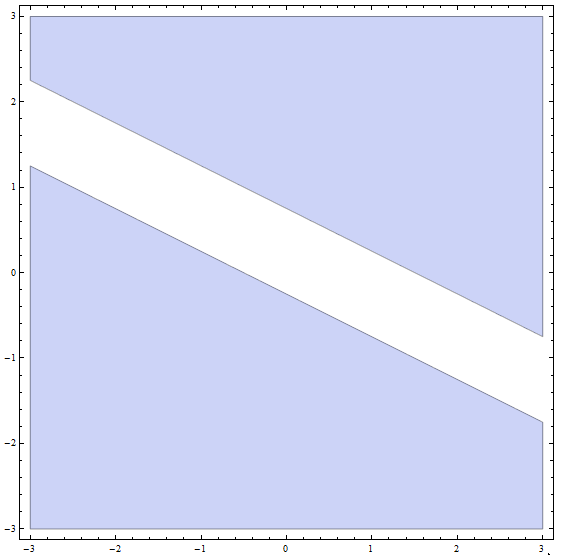
Damit ist die Auflösung der Ungleichung abgeschlossen.
BEISPIEL 2
Lösen Sie die folgende doppelte absolute Absolutwertungleichung
\[| 2x - 1 | \ge |x + 3|\]ANTWORTEN:
Dies ist eine doppelte Absolutwertungleichung, da es 2 Absolutwerte gibt. Dies bedeutet, dass das Finden der Regionen (relativ gesehen) etwas mehr Arbeit erfordert.
Schritt 1: Für den ersten absoluten Wert lösen wir:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]Wir erhalten also \(2x- 1 \ge 0\) auf \([\frac{1}{2}, +\infty)\) und \(2x- 1 < 0\) auf \((-\infty, \frac{1}{2})\).
Für den zweiten absoluten Wert lösen wir:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Wir erhalten also \(x+3 \ge 0\) auf \([-3, +\infty)\) und \(x+3 < 0\) auf \((-\infty, -3)\).
Also definieren wir 4 Regionen:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). In dieser Region erhalten wir: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). In dieser Region erhalten wir: \(2x- 1 \ge 0\) UND \(x+3 < 0\), obwohl diese Region leer ist.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). In dieser Region erhalten wir: \(2x- 1 < 0\) UND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). In dieser Region erhalten wir: \(2x- 1 < 0\) AND \(x+3 < 0\).
Schritt 2: Jetzt müssen wir die doppelte Absolutwertungleichung für jede der vier Regionen lösen:
• Am \(R_1\):
Hier bekommen wir also \(2x- 1 \ge 0\) UND \(x+3 \ge 0\)
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]Um die Teillösung zu erhalten, müssen wir \(x \ge 4\) oder \([4, +\infty)\) mit \(R_1\) schneiden.
Die entsprechende Teillösung lautet daher: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• Am \(R_2\):
Diese Teillösung ist leer (\(\varnothing\)).
• Am \(R_3\):
Hier bekommen wir also \(2x- 1 < 0\) UND \(x+3 \ge 0\)
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]Um diese Teillösung zu erhalten, müssen wir \( x \le -\frac{2}{3}\) oder \( (-\infty, -\frac{2}{3}]\) mit \(R_3\) schneiden.
Die entsprechende Teillösung lautet daher: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• Am \(R_4\):
Hier bekommen wir also \(2x- 1 < 0\) UND \(x+3 < 0\)
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]Um diese Teillösung zu erhalten, müssen wir \( x \le 4 \) oder \((-\infty, 4]\) mit \(R_4\) schneiden.
Die entsprechende Teillösung lautet daher: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Schritt 4:
Schließlich erhalten wir die Vereinigung der Teillösungen, um zu erhalten, dass die Lösung der anfänglich gegebenen Ungleichung ist
Niemand sagte, es würde kurz sein, oder? Gut. Es ist nicht wirklich schwierig, man muss nur systematisch sein und sich an den Plan halten.
Mehr über Ungleichungen mit absolutem Wert
Warum sorgen wir uns überhaupt um diese Art von Ungleichheiten? Wir kümmern uns darum, weil sie Anwendungen in der Praxis haben.
In der Geometrie müssen beispielsweise die Abstände in der realen Linie als absoluter Wert dargestellt werden, da sie nicht negativ sein müssen.
Es könnte eine bestimmte geometrische Situation geben, in der Sie alle Punkte in der realen Linie finden müssen, die mindestens 2 von dem Punkt 3 entfernt sind. Eine solche Situation kann mit der folgenden Ungleichung beschrieben werden:
\[| x-3 |\ge 2\]Lassen Sie uns die obige Ungleichung verstehen. Der Punkt \(x\) ist der Punkt, an dem wir die Ungleichung befriedigen wollen. Der Abstand von \(x\) zum Punkt 3 wird durch \(|x - 3|\) dargestellt.
Dann versuchen wir, die Punkte zu finden, die mindestens 2 von Punkt 3 entfernt sind. Daher muss der Abstand \(|x - 3|\) mindestens 2 betragen, was den \(|x - 3| \ge 2.\) erklärt
Dies ist nur eine Art von Problemen mit absoluten Ungleichheiten, die Sie in der Praxis finden können.
Können Sie absolute Wertungleichungen ohne Lösung finden?
Sie wetten. Hier haben Sie eine \(|2x| < |x|\). Es ist möglich, dass eine Ungleichung einfach nicht durchführbar ist, wie in dem Fall, den ich Ihnen gerade gegeben habe.
Wie wäre es mit der Darstellung von absoluten Ungleichungen?
Der Prozess der grafischen Darstellung geht Hand in Hand mit dem Prozess ihrer Lösung: Sie müssen die Region finden, in denen Sie genau wissen, ob Sie die absoluten Werte positiv oder negativ sind, und dann werden die absoluten Gleichungen zu gleichen Gleichungen. das ist trivial grafisch gezeigt. Dann werden alle Teile der Teilhabenden einfachen einfach.