Substitutionsmethode der Integration
Die Substitutionsmethode der Integration oder der Integrationsmethode durch Substitution ist eine clevere und intuitive Technik, die zum Lösen von Integralen verwendet wird. Sie spielt eine entscheidende Rolle bei der Aufgabe, Integrale zu lösen, zusammen mit der Integration in Teilstücke und Zersetzung von Teilfraktionen Methode.
Die Integration kann manchmal schwierig sein, und wir haben nur wenige Tools zur Verfügung, um damit fortzufahren.
Natürlich ist die Berechnung des unbestimmten Integrals für einige grundlegende Elementarfunktionen (wie Polynome, Potenzen, elementare trigonometrische Funktionen usw.) sehr einfach.
Die Frage ist jedoch, wie mit der Berechnung des unbestimmten Integrals (oder Primitivs) für komplexere Funktionen oder für die algebraische Kombination von Funktionen fortzufahren ist.
Bist du bereit zu rocken?? Ich bin, also folge mir.
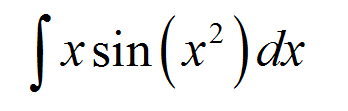
Wie funktioniert die Substitutionsmethode?
Die Methode der Integration durch Substitution funktioniert durch Identifizieren eines "Blocks", der die Integrationsvariable enthält, so dass die Ableitung dieses Blocks auch innerhalb des Integrals gefunden werden kann. Diese Methode wird üblicherweise auch als U-Substitutionsmethode bezeichnet.
Wenn die Struktur des Integrals dies zulässt, wird dieser "Block" tatsächlich zu einer neuen Integrationsvariablen, wenn alles gut läuft, und das Integral wird ernsthaft vereinfacht.
Funktioniert es immer Nein. Oder anders gesagt, Sie können immer eine Substitution durchführen, diese wird jedoch nicht immer in ein einfacheres Integral umgewandelt.
Warum überhaupt diese Methode ausprobieren? Nun, weil es oft funktioniert. Und es ist normalerweise der erste Trick, den Sie versuchen sollten, wenn Sie ein Integral lösen müssen, das nicht trivial ist.
Lassen Sie uns ein paar Schritte ausführen, wenn Sie diese Methode anwenden müssen:
SCHRITT 1:
Untersuchen Sie die Funktion, die Sie integrieren, und suchen Sie nach einem "Block". Dies ist eine Funktion von \(x\), die in der zu integrierenden Funktion ein- oder mehrmals vorkommt.
SCHRITT 2:
Der gesuchte "Block" muss eine ganz bestimmte Eigenschaft haben: Die Ableitung des Blocks muss einmal und nur einmal in der zu integrierenden Funktion erscheinen.
SCHRITT 3:
Wenn die vorherigen Schritte erfolgreich waren, können Sie den "Block" als neue Variable verwenden und die Variable und das Differential durch die neue Variable ersetzen. Das zu lösende Integral wird jetzt viel einfacher.
Technischer Hinweis : Normalerweise versuche ich, alle Erklärungen einfach zu halten und technische Probleme zu vermeiden. In diesem Fall muss ich die technische Erklärung für die Substitutionsmethode geben, um die Idee des "Blocks" nicht zu informell zu machen.
Wenn Sie technische Details nicht mögen, können Sie mit dem nächsten Abschnitt fortfahren, in dem Sie die Beispiele sehen.
Die ganze Idee ist also, eine bestimmte Funktion \(f(x)\) zu integrieren. Also müssen wir finden:
\[\int f(x) \, dx\]Angenommen, die Funktion \(f(x)\) ist nicht irgendeine Funktion und hat eine bestimmte spezifische Struktur, insbesondere
\[f(x) = g(h(x))h'(x)\]und nehmen Sie an, dass es eine Funktion \(G(x)\) gibt, so dass \(G'(x) = g(x)\) (also ist \(G\) das Antiderivativ von \(g\)). Dann bekommen wir das
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]Warum ist das so??? Ganz einfach: Per Definition ist ein Antiderivativ eine Funktion, sodass Sie bei der Differenzierung die Funktion erhalten, die Sie integrieren.
In diesem Fall erhalten Sie, wenn Sie \( G(h(x)) \) unterscheiden
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]nach der Kettenregel ..... und Shazam! Sie haben es. Ich habe dir gesagt, dass es nicht so schwer ist.
Beispiele für die Substitutionsmethoden
Der beste Weg, um zu lernen, wie man sich integriert, ist das Üben. Einige Leute werden sich freuen, Beweise anzuschauen, aber die Mehrheit der Leute wird die Dinge in der Praxis sehen wollen.
Gehen wir also zu praktischen Gründen über.
BEISPIEL 1
Finden Sie das folgende unbestimmte Integral:
\[\int x \sin(x^2)\,dx\]ANTWORTEN:
Gemäß Schritt 1 suchen wir nach einem Block, einem sehr spezifischen Block. Wenn Sie sich das Integral ansehen, lautet die Integrationsvariable \(x\).
Bei Verwendung dieser Technik gibt es möglicherweise viele Versuche und Irrtümer. Angenommen, wir betrachten den folgenden Block:
\[u = x^2\]Wir wissen, dass dieser Block gut ist, weil die Ableitung davon \(u' = 2x\) ist, was im Integral erscheint.
Aber dann sagst du "Ich sehe die \(x\), aber ich sehe die 2 nicht". Nun, es besteht keine Notwendigkeit, angespannt zu sein. Wir können einen Trick machen. Beachten Sie das
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]Wer bist du, Mandrake der Magier ??? Spaß beiseite, dieser kleine Trick funktioniert. Die Blockersetzung ist also
\[u = x^2\] \[du = 2x \, dx\](Die Notation von \(du = 2x \, dx\) ist freizügig und technisch inkorrekt, hat aber eine solide Grundlage. Wenn diese Substitution also das Integral in transformiert
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]Sobald Sie zur neuen Variablen \(u\) gewechselt haben, wurde das Integral zu einem leichter zu lösenden Integral von \(\sin(u)\). Sobald Sie es gelöst haben, MÜSSEN Sie daran denken, zur ursprünglichen Variablen zurückzukehren.
BEISPIEL 2
Kommen wir nun zu einem etwas komplizierteren Beispiel. Berechnen Sie das unbestimmte Integral
\[\int e^{x+e^x} \,dx\]unter Verwendung der U-Substitutionsmethode.
ANTWORTEN:
Was sagst du dazu ??? Nun, es ist nicht so schwer. Beachten Sie, dass das unbestimmte Integral wie folgt umgeschrieben werden kann:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]Können Sie nun, da Sie die neue Form der Funktion sehen, die Sie integrieren, einen "Block" oder eine "U-Substitution" finden?
Denken Sie daran, scheuen Sie sich nicht, Versuch und Irrtum zu machen. Wenn etwas nicht funktioniert, versuchen Sie etwas anderes. Was ist, wenn Sie \(u = e^x\) ausprobiert haben?
Die Ableitung des Blocks ist \(u' = e^x\), die einmal in der ursprünglichen Funktion gefunden wird. Außerdem:
\[u = e^x\] \[du = e^x \, dx\]So bekommen wir:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]Weitere Informationen zur Integration durch Substitution
Seien wir ehrlich: Integration kann schwierig sein. Sehr hart. Einige nicht allzu komplizierte Funktionen (zumindest vom Aussehen her) haben es Mathematikern schrecklich schwer gemacht, damit umzugehen.
Einige andere nicht zu komplizierte Funktionen (zumindest vom Aussehen her wieder) sind mit elementaren Methoden einfach nicht lösbar.
Sie glauben also besser, dass Integration eine schwierige Aufgabe sein kann. Also muss man vorbereitet sein.
Eines der einfachsten und am häufigsten verwendeten Techniken ist die Technik der Integration durch Substitution. Ja, es wird verwendet, weil es häufig bei Tests oder Hausaufgaben vorkommt.
Aber wir haben ein bisschen geschummelt. In der Realität sind Integrale, die die richtige Struktur haben, um durch die Substitutionstechnik gelöst zu werden, sehr spezifisch. Der Grund, warum Sie viele Beispiele dafür sehen, ist, dass es sich um sehr spezifische Funktionen handelt, die funktionieren sollen, um in diese Technik integriert zu werden.
Aber lassen Sie mich stumpf sein: Wenn Sie ein Softwareprogramm haben, das zufällige Funktionen generiert und eine für Sie generiert, sind die Chancen gering, dass Sie die Substitutionstechnik verwenden können.
Dennoch ist es eine leistungsstarke kleine Integrationstechnik, die für eine ganz bestimmte Klasse von Integralen funktioniert.
Was ist die U-Substitutionstechnik?
Die 𝘶-Substitution mit unbestimmten Integralen ist nur ein anderer Name für die Substitutionsmethode. Es heißt "𝘶-Substitution", da der verwendete Block \(u\) heißt, die neue Variable also u ist.
Dies ist definitiv kein guter Name, da der Name, den Sie für Ihren Block wählen, für den Prozess der Berechnung des Integrals völlig irrelevant ist. Sie können den Block (und Ihre neue Variable) \(z\) aufrufen und es würde keinen Unterschied machen.