Solventes Álgebra

Fórmula da inclinação

Instruções: Use esta calculadora para calcular a fórmula da inclinação, para quaisquer dois pontos que você fornecer, mostrando todas as etapas. Por favor, digite dois pontos do formulário (x, y) na caixa de formulário abaixo.

Mais sobre a fórmula da inclinação

Isto Fórmula de inclinação A calculadora permitirá que você calcule a inclinação para dois pontos dados da forma (x, y) usando a conhecida fórmula, mostrando todas as etapas.

Você precisa fornecer dois pontos do formulário (x, y). Por exemplo, você pode fornecer pontos como (1/2, 1/3) ou algo que não seja simplificado como (1/3+1/4, sqrt(8)).

Depois de fornecer dois pontos válidos do formulário (x, y), o próximo passo é clicar no botão que diz "Calcular" e você receberá todas as etapas dos cálculos da fórmula de inclinação.

O conceito de inclinação é crucial em Álgebra e Geometria, e a inclinação é muito importante para a construção de uma Função linear .

Qual é a fórmula da inclinação?

Suponha que temos dois pontos \((x_1, y_1)\) e \((x_2, y_2)\) no plano. Então o fórmula da inclinação é :

\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]

Algumas pessoas dirão "é a razão entre a diferença de y's e a diferença de x's", com a ressalva de que você precisa preservar a ordem ao fazer as diferenças. Se em cima você faz \(y_2 - y_1\), então em baixo você faz \(x_2 - x_1\) e não \(x_1 - x_2\).

Além disso, algumas pessoas chamam essa fórmula de inclinação de "Subida versus Corrida"/

Quais são as etapas para usar a fórmula da inclinação

Passo 1: Identifique os dois pontos dados. É uma boa ideia simplificar as expressões o máximo possível, antes de usar a fórmula
Etapa 2: determine qual é o primeiro ponto e qual é o segundo. A escolha é irrelevante para o resultado, desde que você permaneça consistente com sua escolha
Passo 3: Use a fórmula \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\) inserindo os valores do primeiro ponto \(x_1\) e \(y_1\), e do segundo ponto \(x_2\) e \(y_2\)
Etapa 4: depois de inserir os valores, simplifique o máximo possível para reduzir a inclinação à sua forma mais simples

O cálculo da inclinação usando a fórmula geralmente é um processo muito simples, apenas certifique-se de manter consistente a ordem dos pontos.

Como usar a inclinação?

A inclinação é uma medida da inclinação de uma linha. De fato, quando você tem uma função linear da forma

\[y = m x + n\]

então, a inclinação da linha é m. O acima é conhecido como forma de intercepção de encostas de uma linha.

Quais são as etapas para usar a inclinação de uma linha?

Passo 1: Identifique a inclinação m. Simplifique o máximo possível
Etapa 2: você precisa conhecer a interceptação y, ou seja, o ponto no eixo y quando a linha o cruza e chamá-lo de n
Passo 3: Então, a equação da reta é \(y = m x + n\)

Existem outras formas de expressar a linha além da Interceptação de Inclinação . Você tem a formulário padrão da linha , e as Forma ponto-inclinação .

Como usar a fórmula de interceptação de inclinação

Esse é o centro de funções lineares (ou afim linear, deveríamos dizer) e grafos lineares. De fato, quando você tem a inclinação m e a interceptação y n, você calcula diretamente a equação da linha como y = mx + n.

Geometricamente, isso é bastante simples de interpretar, pois a interceptação y é absolutamente clara como o ponto de interseção entre a linha e o eixo y, e a inclinação é a medida da inclinação. Como referência, uma inclinação de m = 1 corresponde a uma inclinação de 45 ^o .

Por outro lado, se você tiver algum Função linear , Através dos Simplificação Algébrica você sempre pode reduzir para a forma de interceptação de inclinação y = mx + n, e então você encontrou sua inclinação m e interceptação de y n.

Exemplo: usando a fórmula da inclinação

Calcule a inclinação para os seguintes pontos: \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) e \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)

Solução: Precisamos calcular a inclinação de uma reta que passa pelos pontos \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) e \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\).

A seguinte fórmula é necessária para calcular a inclinação dados os dois pontos:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Agora, substituindo os valores dos pontos \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) e \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) leva a:

\( \displaystyle m = \frac{\frac{7}{4}-\frac{5}{4}}{\frac{7}{3}-\frac{1}{3}}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 7}{ 4}-\frac{ 5}{ 4}=\frac{ 7-5}{ 4}=\frac{ 2}{ 4}=\frac{ 2}{ 2 \times 2}=\frac{ \cancel{ 2}}{ \cancel{ 2} \times 2}=\frac{ 1}{ 2}\) and \(\displaystyle \frac{ 7}{ 3}-\frac{ 1}{ 3}=\frac{ 7-1}{ 3}=\frac{ 6}{ 3}=\frac{ 3 \times 2}{ 3}=\frac{ \cancel{ 3} \times 2}{ \cancel{ 3}}=2\)

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{2}}{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 1}{ 2} \times \frac{ 1}{ 2}=\frac{ 1}{ 2 \times 2}=\frac{ 1}{ 4}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\)

Portanto, concluímos que a inclinação de uma reta que passa pelos pontos \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) e \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) é \(m = \displaystyle \frac{1}{4}\).

Exemplo: mais exemplos da fórmula de inclinação

Use a fórmula de inclinação para encontrar a inclinação da linha que passa pelos pontos: \((2, 4)\) e \((5, 12)\)

Solução: Neste caso temos os pontos \(\displaystyle (x_1, y_1) = \left(2,4\right)\) e \(\displaystyle (x_2, y_2) = \left(5,12\right)\), que são os pontos pelos quais sabemos que a reta passa.

A fórmula da inclinação é:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Agora, substituindo os valores dos pontos \(\displaystyle (x_1, y_1) = \left(2,4\right)\) e \(\displaystyle (x_2, y_2) = \left(5,12\right)\) leva a:

\(\displaystyle m = \frac{12-4}{5-2}\)

\( = \)

\(\displaystyle \frac{8}{3}\)

Reducing the integers that can be subtracted together: \(\displaystyle 12-4 = 8\), \(\displaystyle 5-2 = 3\)

Portanto, concluímos que a inclinação de uma reta que passa pelos pontos \(\displaystyle (x_1, y_1) = \left(2,4\right)\) e \(\displaystyle (x_2, y_2) = \left(5,12\right)\) é \(m = \displaystyle \frac{8}{3}\).

Exemplo: formulário de interceptação de inclinação

Encontre a forma de interceptação da inclinação para a seguinte linha: \(2x + 4y = 3 + \frac{1}{2}x\).

Solução: Temos a seguinte equação:

\[\displaystyle 2x+4y=3+\frac{1}{2}x\]

Colocando \(y\) no lado esquerdo e \(x\) e a constante no lado direito obtemos

\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]

Agora, o termo multiplicando \(y\) é \( 4 - 0 = 4\), e também desde \( \frac{1}{2} - 2 = -\frac{3}{2}\), obtém-se o seguinte

\[\displaystyle 4y=-\frac{3}{2}x+3\]

Agora, resolvendo para \(y\), dividindo ambos os lados da equação por \(4\), obtém-se o seguinte

\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]

e simplificando, finalmente obtemos o seguinte

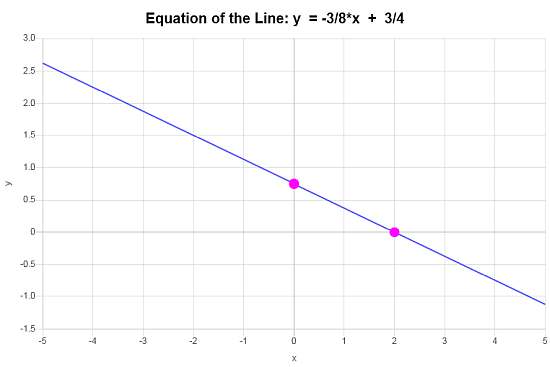
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]

Conclusão : Com base nos dados fornecidos, concluímos que a equação da linha na forma inclinação-intersecção é \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\), com uma inclinação de \(\displaystyle b = -\frac{3}{8}\) e intersecção y de \(\displaystyle n = \frac{3}{4}\).

Graficamente, a linha se parece com:

Outras calculadoras de funções lineares

Junto com funções quadráticas , as funções lineares estão entre os objetos mais importantes da matemática. você pode calcular a inclinação de uma linha, encontrar o linha perpendicular , e converter a linha entre diferentes formas, dependendo das necessidades.

Uma coisa notável para funções lineares é que é mais fácil encontrar funções lineares inversas , já que a maioria das funções lineares são de 1 para 1 (exceto para linhas horizontais).