Saiba mais sobre esta calculadora de linhas perpendiculares.

As linhas estão em grande parte determinadas pelo seu declive (inclinação). As linhas horizontais são linhas com inclinação igual a zero, uma linha vertical são linhas onde a inclinação é indefinida (infinito negativo ou positivo).

As linhas perpendiculares são linhas que se cruzam formando um ângulo recto. Existe uma condição específica para a inclinação e o declive perpendicular sempre que as encostas forem definidas, para que as linhas sejam perpendiculares, ou seja, que o produto das encostas seja -1.

Observar que uma dada linha tem infinitas linhas perpendiculares a ela. A fim de encontrar aquela que procura, é necessário fixar um ponto pelo qual passa.

Como é que se encontra a linha perpendicular de uma linha?

A estratégia é simples. O passo é encontrar o declive da linha dada. Se lhe for fornecida a inclinação e intercepção para definir a linha, então já tem a inclinação.

Caso contrário, talvez tenha dois pontos por onde a linha passa neste caso, pode calcular directamente a inclinação.

Em última análise, se definir a sua linha dada com uma equação, precisa de colocar essa equação no forma de intercepção de encostas , de modo a obter a encosta.

Uma vez que se tem a inclinação da linha dada, usa-se a fórmula para a inclinação perpendicular, multiplicando por menos um a inclinação recíproca da inclinação original.

O que é a linha perpendicular de uma linha horizontal

A linha perpendicular a uma linha horizontal é uma linha vertical.

O que é a linha perpendicular de uma linha vertical

A linha perpendicular a uma linha vertical é uma linha horizontal.

É possível calcular a linha perpendicular sem pontos

Quando se tem uma linha, não há uma, mas muitas (infinitas) linhas perpendiculares à linha dada. A fim de identificar uma linha perpendicular específica, é necessário fornecer um ponto por onde a linha passa.

Tipicamente, fornecerá um ponto na linha original, onde quer que a linha perpendicular passe.

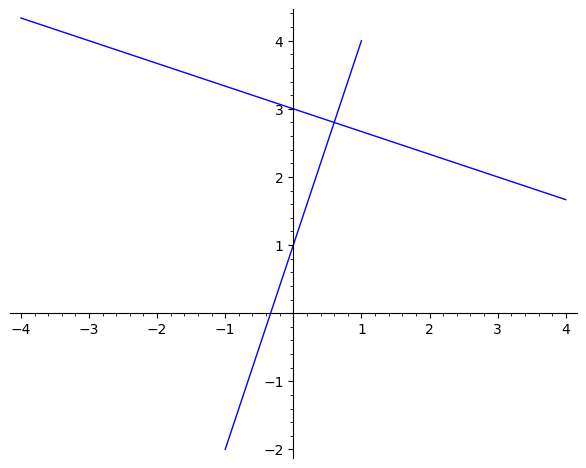
Exemplo do cálculo de uma linha perpendicular para uma dada linha:

Considerar a linha com a equação <$2x + 3y = 5)$>. Encontrar a equação da linha perpendicular que passa por <$(1, 1)$>>.

Solução: Primeiro obtemos a equação de intercepção de encosta para a linha GIVEN, se possível

Foi-nos fornecida a seguinte equação:

$$\displaystyle 2x+3y=5$$

Colocando $y$ no lado esquerdo e $x$ e a constante no lado direito obtemos

$$\displaystyle 3y = -2x +5$$

Depois, resolvendo para $y$, dividindo ambos os lados da equação por $3$, obtém-se o seguinte

$$\displaystyle y=-\frac{2}{3}x+\frac{5}{3}$$

Fórmula De Declive Perpendicular

Em geral, a fórmula necessária para calcular a inclinação perpendicular, <$m_{\perp}$, é:

$$m_{\perp} = \displaystyle -\frac{1}{m}$$

Ao ligar o valor de $m =$ na fórmula, verificamos que a inclinação perpendicular é

$$m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{} = \frac{3}{2}$$

Construção De Linhas Perpendiculares

Agora, calculámos que a inclinação perpendicular é <$m_{\perp} = \frac{3}{2}$ o e sabemos que a linha perpendicular passa pelo ponto $(1, 1)$>>.

Assim, com a informação de que dispomos, podemos construir directamente a forma pontiaguda da linha, que é

$$\displaystyle y - y_1 = m_{\perp} \left(x - x_1\right)$$

e depois ligando os valores conhecidos de <$\displaystyle m_{\perp} = \frac{3}{2}$ e $\displaystyle \left( x_1, y_1 \right) = \left( 1, 1\right)$, obtemos que

$$\displaystyle y-1 = \frac{3}{2} \left(x-1\right)$$

Agora, precisamos de expandir o lado direito da equação, distribuindo a inclinação, de modo a obter $$\displaystyle y = \frac{3}{2} x + \frac{3}{2} \left(-1\right) + 1$$>

e simplificando, vamos obter que <$$\displaystyle y=\frac{3}{2}x-\frac{1}{2}$$>>>

Portanto, concluímos que a equação da linha dada é $\displaystyle y=-\frac{2}{3}x+\frac{5}{3}$ e a equação da linha perpendicular é $\displaystyle y=\frac{3}{2}x-\frac{1}{2}$>>.

Se quiser tornar as coisas mais directas, use isto Calculadora de inclinações perpendiculares e usar a fórmula da linha perpendicular para obter directamente a inclinação da linha que é a linha perpendicular.

Isso é para o caso de só ser à procura da encosta no contexto do que se está a fazer.