Como utilizar esta calculadora de taludes com degraus

Utilize esta calculadora para encontrar o declive de uma linha que fornece, com todos os passos mostrados.

O declive é uma medida da inclinação da linha em relação aos eixos coordenados. Uma inclinação positiva indica que a linha tem uma inclinação ascendente, enquanto que uma inclinação negativa indica que a linha tem uma inclinação descendente.

Um declive igual a zero indica que a linha é horizontal, enquanto que uma linha vertical não tem um declive bem definido.

Como calcular uma inclinação?

Normalmente, o cálculo da inclinação é fácil, mas existem várias maneiras de calcular uma inclinação e tudo depende de quais informações são fornecidas e como são fornecidas.

A maneira mais comum de apresentar um cálculo de inclinação é primeiro fornecer uma equação linear para a qual você precisa encontrar sua inclinação ou quando eles fornecem dois pontos pelos quais uma linha passa.

Calculadora de inclinação da equação: encontrando a inclinação da linha

Esta calculadora mostrará como calcular a inclinação de uma linha que você fornecer, e você terá diferentes maneiras de indicar e definir sua linha. Ele também lhe dará um gráfico refletindo a inclinação calculada.

Por exemplo, uma forma comum é definir a sua linha dando uma equação, e então terá esta calculadora para calcular a inclinação a partir da equação.

A estratégia geral para isso é colocar a equação da linha na forma de inclinação-intercepção , a partir do qual é fácil reconhecer a inclinação da estrutura da equação \(y = mx + n\).

Esta é uma inclinação da calculadora de dois pontos também

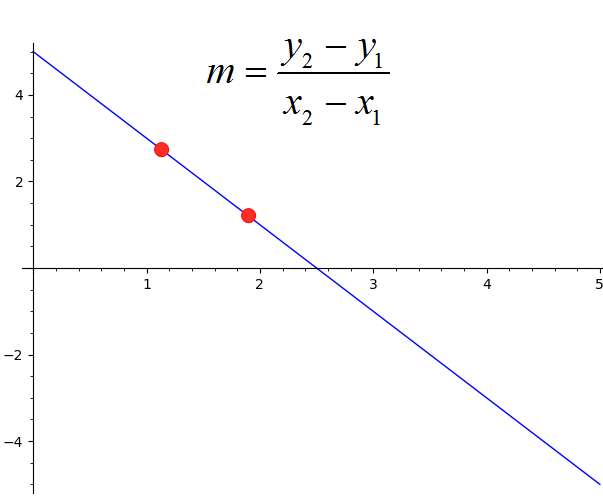
Talvez uma das formas mais comuns de calcular o declive seja quando se definir a equação, fornecendo dois pontos como \((x_1, y_1)\), \((x_2, y_2)\). Então, como você encontra a inclinação de dois pontos? A inclinação é simplesmente calculada como

\[m = \frac{y_2-y_1}{x_2-x_1}\]

que é como encontrar a inclinação de dois pontos. Não vamos esquecer que esses dois pontos geralmente são pontos por onde passa uma linha, então você está encontrando a inclinação da linha que passa por esses pontos.

Em última análise, como encontrar o declive de uma linha dependerá de como a linha é definida. Esta calculadora irá cobri-lo com todos os casos, mesmo quando existem fracções no cálculo.

Interpretação: o que é uma inclinação de 2%?

Existem várias maneiras de ver isso, mas uma forma comum é pensar que para cada aumento de 100 unidades em X, a reta aumenta 2 unidades em Y, o que explica 2/100 = 0,02 = 2%.

Na mesma linha de interpretação, pode-se dizer que uma inclinação de 45% é tal que um aumento de 100 unidades em X leva a um aumento de 45 unidades em Y. Observe que isso NÃO é o mesmo que uma inclinação com 45. ^o graus.

Calculadora instantânea de inclinação

A ideia de uma calculadora de inclinação é simples quando você considera dois pontos, caso em que você usa a fórmula acima. Mas qual é a inclinação instantânea? Isso se refere à inclinação quando os dois pontos se tornam cada vez mais próximos.

Então você quer ver qual valor a inclinação se aproxima também, quando os dois pontos se aproximam juntos. A ideia de inclinação instantânea é refletida por este calculadora derivada , que é essencialmente calcular inclinações instantâneas.

Exemplo: cálculo da inclinação

Suponha que você tenha uma linha com o seguinte formato padrão \( \frac{3}{4} x + 2y = 6\). Encontre a inclinação da linha.

Solução: Cálculo da inclinação de uma linha

Foi-nos fornecida a seguinte equação:

\[\displaystyle \frac{3}{4}x+2y=6\]

Colocando \(y\) no lado esquerdo e \(x\) e a constante no lado direito obtemos

\[\displaystyle 2y = -\frac{3}{4}x +6\]

Agora, resolvendo para \(y\), dividindo ambos os lados da equação por \(2\), obtém-se o seguinte

\[\displaystyle y=-\frac{\frac{3}{4}}{2}x+\frac{6}{2}\]

e simplificando, finalmente obtemos o seguinte

\[\displaystyle y=-\frac{3}{8}x+3\]

Conclusão : Com base nos dados fornecidos, concluímos que a inclinação da reta é \(\displaystyle m = -\frac{3}{8}\).

Exemplo: cálculo da inclinação a partir de dois pontos

Suponha que você tenha uma linha que passa por 2 pontos: \( (1, 2)\) e \( (4, 11/3)\). Encontre a inclinação da linha.

Solução:

Cálculo da inclinação de uma linha

A informação fornecida sobre a linha é que a linha passa pelos pontos\(\displaystyle \left( 1, 2\right)\) e \(\displaystyle \left( 4, \frac{11}{3}\right)\)

Portanto, o primeiro passo consiste em calcular a inclinação. A fórmula para a inclinação é: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]

Agora, substituindo os números correspondentes, obtemos que a inclinação é: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{11}{3} - 2}{ \displaystyle 4 - 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]

Então, descobrimos que a inclinação é \(\displaystyle m = \frac{5}{9}\) e que a reta passa pelo ponto \(\displaystyle \left( 1, 2\right)\)

Conclusão : Com base nos dados fornecidos, concluímos que a inclinação da reta é \(\displaystyle m = \frac{5}{9}\).

O declive de uma linha é uma das suas propriedades mais importantes, juntamente com a Y-Intercept e x-intercepção porque, essencialmente, definem a linha.