Mais sobre desigualdades polinomiais

Esta calculadora pode ajudá-lo na solução de inequações polinomiais, mostrando todas as etapas do processo de cálculo da solução, além de fornecer um gráfico de desigualdade, representando a solução

A desigualdade que você fornece pode ser algo simples como 'x^2 > 1', ou pode ser algo mais complexo como 'x^3 + 3x^2 + 3x + 1 > 0'.

Uma vez fornecida a desigualdade polinomial válida, vá em frente e clique no botão "Calcular", para obter a solução e todos os passos mostrados.

Esteja ciente de que nem todos os polinômios fornecidos serão adequados para soluções exatas. Quanto menor o grau do polinômio, maior a probabilidade de ser encontrada uma solução exata para a desigualdade.

O que é uma desigualdade polinomial

Uma desigualdade polinomial é simplesmente um tipo de desigualdade em que as expressões envolvidas são polinomiais e nenhum de seus termos é uma expressão não polinomial. Por exemplo

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

é uma desigualdade polinomial, enquanto

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

é um não, devido à presença do termo \(\sin x\), que não é um polinômio. Resolvendo Desigualdades em geral é um processo difícil em geral, mas para os polinomiais temos um plano de ação claro.

Como você resolve uma desigualdade polinomial

• Passo 1: Certifique-se de que todos os termos sejam polinômios. Caso contrário, os métodos específicos usados para polinômios podem não ser aplicáveis
• Passo 2: Coloque tudo de um lado, deixando zero do outro lado
• Estágio 3: Substituindo o sinal de desigualdade por "=", resolva a equação associada (isso envolve encontrar os zeros de um polinômio)
• Passo 4: Colete todos os pontos críticos da desigualdade, que neste caso são os zeros reais do auxiliar Equação Polinomial (você não considera as raízes complexas neste caso)
• Etapa 5: Se não existirem pontos críticos, isso implica que a expressão não muda de sinal, então toda a reta real será uma solução, ou não, não há solução. Para verificar, escolha qualquer ponto e veja se satisfaz a desigualdade, e se satisfaz, toda a reta real é a solução, caso contrário, não há solução
• Etapa 6: Se houver pontos críticos, construa intervalos com pontos críticos consecutivos (usando -∞ como ponto crítico inicial e ∞ como ponto crítico final)
• Estágio 7: Verifique cada um desses intervalos e veja se um ponto interno atende à desigualdade. Se isso acontecer, o intervalo faz parte da solução; caso contrário, o intervalo não faz parte da solução.

A ideia chave aqui é que os pontos críticos e os intervalos que derivamos deles são intervalos para os quais a expressão não muda de sinal, portanto, ou todo o intervalo é uma solução, ou nenhum ponto no intervalo faz parte da solução.

Zeros polinomiais e pontos críticos

Uma das razões pelas quais a resolução de desigualdades polinomiais é possível é porque é relativamente simples analisar expressões polinomiais para pontos críticos, além do fato de que polinômios são expressões contínuas.

Haverá desigualdades como

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

em que será muito mais difícil encontrar pontos críticos. desigualdades lineares são ainda mais simples de encontrar pontos críticos, mas isso é tudo. Qualquer desigualdade geral apresentará as suas próprias complexidades.

Aplicações de polinômios na vida real

Existem muitas aplicações de polinômios. Por exemplo, em Física, quando você estuda Cinemática, existem algumas expressões polinomiais interessantes derivadas das Leis de Newton. Estas expressões podem definir condições para a posição de um corpo, o que poderia levar a uma desigualdade polinomial para determinar em que momentos o corpo está acima de determinada altura, o que poderia ser crucial em balística, por exemplo.

Além disso, ao estudar Equações Diferenciais, você pode encontrar termos dumpering na equação que dependem de uma potência e possuem estrutura polinomial, para os quais você pode usar algumas desigualdades avançadas, como as Desigualdades de Gronwall.

Exemplo: resolvendo desigualdades polinomiais

Resolva: \(x^2 - x > \frac{1}{2}\)

Solução: Precisamos primeiro resolver a seguinte equação quadrática \(\displaystyle x^2-x-\frac{1}{2}=0\):

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

então, descobrimos que:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Análise de pontos críticos

A lista de pontos críticos encontrados organizados em ordem crescente é: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Com base nisso, precisamos analisar os seguintes intervalos:

• Para o intervalo \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): O lado esquerdo é positivo, então \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) faz parte da solução.

• Para o intervalo \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): O lado esquerdo é negativo, o que significa que \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) não faz parte da solução.

• Para o intervalo \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): O lado esquerdo é positivo, o que significa que \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) faz parte da solução.

Solução para a desigualdade

Com base na desigualdade fornecida, e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) ou \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Usando a notação de intervalo, a solução é escrita como:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]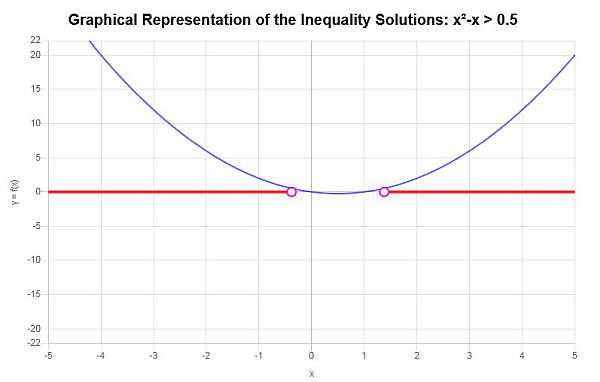

que conclui o cálculo.

Exemplo: polinômio de grau superior

Resolva a seguinte desigualdade: \(x^3 - x > 1\)

Solução:

Para resolver \(x^3-x > 1\) primeiro colocamos tudo de lado:

\[x^3-x-1> 0\]

Agora, a partir disso obtemos a equação associada que precisa ser resolvida primeiro, que é \(x^3-x-1=0\). Observe que o grau é \(\displaystyle deg(p) = 3\), seu coeficiente líder é \(\displaystyle a_{3} = 1\) e seu coeficiente constante é \(\displaystyle a_0 = -1\).

Tentando raízes racionais

Tentaremos primeiro encontrar raízes racionais simples, com o Teorema do Zero Racional.

A próxima tarefa é encontrar os números inteiros que dividem o coeficiente líder \(a_{3}\) e o coeficiente constante \(a_0\), que serão usados para construir nossos candidatos a zeros da equação polinomial.

▹ Os divisores de \(a_{3} = 1\) são: \(\pm 1\).

▹ Os divisores de \(a_0 = -1\) são: \(\pm 1\).

Portanto, dividindo cada divisor do coeficiente constante \(a_0 = -1\) por cada divisor do coeficiente líder \(a_{3} = 1\), encontramos a seguinte lista de candidatos a raízes:

\[\pm \frac{ 1}{ 1}\]

Agora, todos os candidatos precisam ser testados para ver se são uma solução. O seguinte é obtido a partir do teste de cada candidato:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

Mas como não encontramos raízes racionais por inspeção, não podemos continuar com a fatoração usando métodos elementares, então o processo para aqui.

OPCIONAL : Este é um polinômio de grau \(3\), para o qual há um total de raízes \(3\), mesmo que algumas possam ser complexas, mas neste caso menos de \(3\) soluções foram encontradas usando métodos elementares.

Usando métodos avançados de equações cúbicas, pode-se descobrir que o conjunto completo de soluções é:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Análise de pontos críticos

O único ponto crítico encontrado é \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

Com base nisso, precisamos analisar os seguintes intervalos:

• Para o intervalo \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): O lado esquerdo é negativo, então \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) não faz parte da solução.

• Para o intervalo \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): O lado esquerdo é positivo, o que implica que \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) faz parte da solução.

Solução para a desigualdade

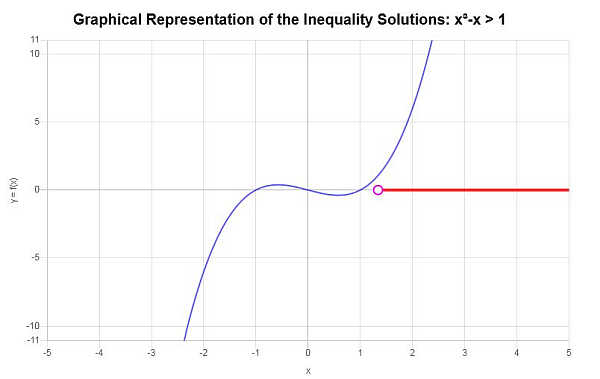
Com base na desigualdade fornecida e analisando os pontos críticos, descobrimos que a solução para a desigualdade é: \(x > 1.3247180451128\).

Usando a notação de intervalo, a solução é escrita como:

\[\left(1.3247180451128,\infty\right)\]

Graficamente:

Mais calculadoras de desigualdade

Resolvendo Desigualdades (proibido de encontrar soluções para equações ) é uma das operações mais comuns em matemática, em todos os aspectos.

O processo de resolução de desigualdades costuma ser trabalhoso e, em geral, não existe uma regra para resolvê-las. Resolvendo desigualdades polinomiais é uma das poucas exceções, em que podemos seguir um conjunto de passos para encontrar as soluções, mas ainda assim podemos falhar, porque polinômios de grau superior são difíceis de lidar. Na verdade, é realmente impossível encontrar raízes polinomiais acima do grau 5 usando uma regra geral (Teorema de Abel).