Mais sobre derivados trig

Use esta calculadora para encontrar derivadas trigonométricas, que neste caso assumimos como qualquer função diferenciável válida que envolva uma ou mais funções trigonométricas elementares.

Um exemplo de uma função válida para esta calculadora é f(x) = sin(x)/x, ou f(x) = x*sin(x^3), apenas para dar um exemplo.

Então, quando você já digitou a função correspondente, você pode clicar no botão "Calcular", para obter todas as etapas do cálculo da derivada mostrada a você.

As funções trigonométricas desempenham um papel crucial no cálculo, bem como na calculando derivativos em geral. Por fim, funções mais complexas podem ter suas derivadas reduzidas ao cálculo da derivada para funções trigonométricas mais simples.

Derivados trig básicos

A ideia de usar regras derivadas é quebrar uma função complexa e diferenciá-la usando as derivadas de funções conhecidas. Especificamente, funções trigonométricas simples como seno, cosseno, tangente e cotangente desempenharão um papel importante nisso.

Quais são as derivadas trigonométricas básicas?

• Derivada Trigonométrica 1: $\frac{d}{dx} \sin (x) = \cos(x)$>
• Derivada Trigonométrica 2: $\frac{d}{dx} \cos (x) = -\sin(x)$>
• Derivada Trigonométrica 3: $\frac{d}{dx} \tan (x) = \sec^2(x)$>
• Derivada Trigonométrica 4: $\frac{d}{dx} \cot (x) = -\csc^2(x)$>
• Derivada Trigonométrica 5: $\frac{d}{dx} \sec (x) = \sec(x)\tan(x)$>
• Derivada Trigonométrica 6: $\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)$>

Estas são as derivadas básicas que você precisa saber muito e possivelmente memorizar para usar Regras de Derivadas para calcular derivadas mais complicadas

As derivadas trigonométricas estão em graus?

Não, a derivada das funções trigonométricas estão em radianos , então as derivadas trigonométricas encontradas refletem o fato de que o argumento x é medido em radianos.

Assim, por exemplo, suponha que queremos calcular a derivada do pecado em graus , então definimos $f(y) = \sin(y)$, onde $y$ é medido em graus.

Agora, seja $x = \frac{\pi y}{180}$ o ângulo equivalente em radianos e também resolvendo para $y$ encontramos que $y = \frac{180 x}{\pi}$, então usando a Regra da Cadeia:

$$\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y)$$

Com base nisso, a derivada do seno em graus é, na verdade, cosseno em graus, mas vezes um fator $\frac{180}{\pi}$.

Como você encontra derivadas em trigonometria?

Derivados trigonométricos são encontrados por definição, usando identidades trigonométricas básicas. Por exemplo, usando o seno da fórmula da soma podemos derivar a derivada de $\sin(x)$, usando a definição de limite:

$$\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h}$$ $$\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right)$$ $$\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)$$

Dicas e truques

A principal lição para você é sempre lembrar o que o 6 derivadas trigonométricas são , e saiba-os de cor, pois você os usará continuamente, junto com o básico regras de diferenciação .

Da mesma forma, você pode usar identidades trigonométricas e a definição de função inversa para encontrar as derivadas trigonométricas inversas mais comuns.

Exemplo: cálculo da derivada trig

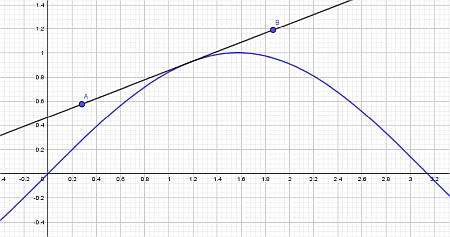
Considere a seguinte função: $f(x) = \sin^2(x)+ \frac{1}{x}$. Encontre sua derivada

Solução: Derivadas trigonométricas envolvem funções trigonométricas que precisam ser diferenciadas. Considere a função $\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}$, que contém uma função seno, portanto ela se qualifica como uma derivada trigonométrica.

Resultados : Para este exemplo, verifica-se que a derivada é:

$$f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}$$

É muito útil representar a função e sua derivada em um gráfico. Veja abaixo:

Exemplo a derivada de uma função trigonométrica

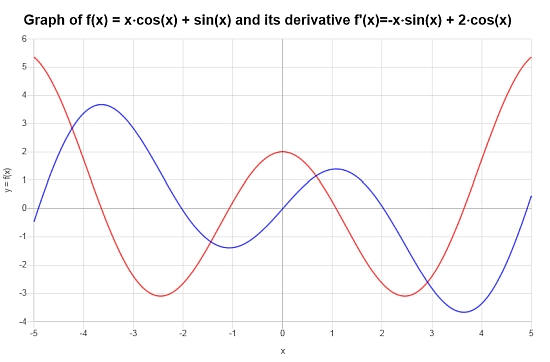
Considere a seguinte função trigonométrica: $f(x) = \sin(x) + x \cos(x)$, encontre sua derivada.

Solução: Agora, precisamos trabalhar com a derivada da seguinte função trigonométrica $\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)$.

Conclusão Final : Concluímos que a derivada é dada por:

$$f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)$$

Obtém-se o seguinte gráfico:

Exemplo: derivadas trigonométricas e diferenciação implícita

Encontre $\frac{dy}{dx}$ para $\sin(x)+\cos(y) = 1$.

Solução: precisamos usar diferenciação implícita , então diferenciamos ambos os lados e usamos o Regra Da Cadeia :

$$\frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right)$$ $$\Rightarrow \cos(x)-\sin(y)y' = 0$$ $$\Rightarrow \sin(y)y' = \cos(x)$$ $$\Rightarrow y' = \frac{\cos(x)}{\sin(y)}$$

que conclui o cálculo.

Outras calculadoras de derivadas úteis

encontrando a derivada de funções simples e elementares é a pedra angular do processo de encontrar as derivadas de funções mais complicadas, através do uso do conhecido regras de diferenciação .

Neste contexto, o básico funções trigonométricas podem ser consideradas funções elementares para as quais a derivada pode ser calculada por limites, via sua própria definição. Entre as funções elementares mais úteis temos polinômios e funções racionais.