Sobre esta calculadora de pecado

Esse calculadora de pecado fará o seguinte para você: você pode fornecer uma expressão numérica como sin(pi/4), caso em que a calculadora irá simplificá-la e fornecerá um valor numérico aproximado, se necessário. Além disso, se você fornecer uma função sen como sin(3x+1), a calculadora fará o gráfico dela.

Então, o processo é simples: depois de fornecer o expressão de pecado deseja calcular, basta clicar no botão "Calcular" que está abaixo do formulário para obter os passos da solução.

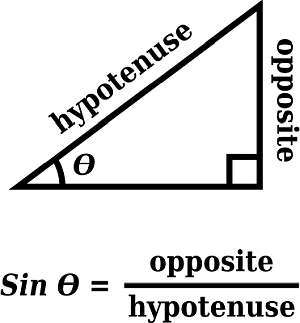
Seno, juntamente com cosseno são dois pilares da trigonometria. Você verá seno e cosseno ao redor quando resolver triângulos , por exemplo, mas também em áreas como a Física.

Como você calcula o pecado?

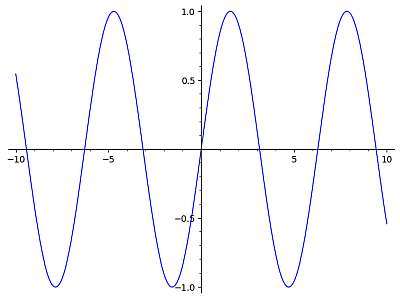
O pecado é um dos blocos de construção básicos em Geometria e Trigonometria. Sin é uma quantidade que pode ser calculada para ângulos no contexto de um triângulo retângulo. Quando você tem um dos ângulos em um triângulo retângulo que não é o 90 _o um, você pode encontrar o lado oposto e a lado adjacente .

Então, a fórmula para o pecado é

\[\sin \theta = \frac{\text{Opposite Side} }{ \text{Hypothenuse} }\]

O que é pecado igual?

Sin é uma quantidade adimensional, que mede o tamanho da inclinação de um ângulo em relação à referência horizontal, onde o lado adjacente está sentado.

Quando sen é zero, então o ângulo é zero, então não há abertura. A abertura máxima do ângulo ocorre quando sin = 1, que ocorre em 90 _o .

Qual é o pecado de 1?

Essa pergunta pode parecer inocente, mas muitas vezes leva à confusão. Na matemática formal, todas as funções trigonométricas serão medidas em radianos por padrão. Mas, por alguma razão, os radianos não são muito conhecidos ou muito populares entre os estudantes, que preferem usar graus como medida, porque é simplesmente mais familiar.

Os alunos conhecem bem os ângulos notáveis em graus como 90 _o sendo o ângulo reto, e 360 _o sendo o círculo completo. você pode usar isso calculadora de grau para radiano para se mover entre os dois sistemas.

Portanto, a resposta correta para o que é sen(1) é que sen(1) é aproximadamente 0,841471, quando se assume que o ângulo 1 está em radianos. Agora, sin(1) é aproximadamente 0,017452 quando se assume que 1 é expresso em graus. Então, extremo cuidado deve ser exercido ao lidar com ângulos.

Quanto é seno elevado a menos 1?

Outra questão que formalmente tem uma resposta simples, mas às vezes depende da convenção utilizada. O seno elevado a 1 negativo precisa ser mais especificado, pois o seno é uma função. Então você pode fazer sin(1), e isso é um número, e sin(1) elevado a menos 1 é apenas pegar o inverso do número sin(1), então você tem 1/sin(1), que é um número.

Muitas vezes, porém, seno elevado a menos 1 significa referir-se à 'função inversa do seno', que é conhecida como função arcsin, ou às vezes algumas pessoas gostam de usar a nomenclatura de \(sin^{-1}(x)\).

Posso usar uma calculadora científica para calcular o pecado

De fato você pode, mas uma vantagem de usar isso calculadora de pecado é que você obterá as etapas mostradas junto com o resultado. A maioria das calculadoras mostrará apenas a resposta final.

Como usar uma calculadora de pecado?

A ideia principal de uma calculadora de pecado é avaliar as expressões de pecado que você fornece. Existem alguns ângulos notáveis, geralmente múltiplos ou frações de \(\pi\) que são resultados simples, inteiros ou fracionais ao calcular seus senos, portanto, é uma boa ideia usar uma calculadora de expressão senil para ajudá-lo com isso.

Não é fácil lembrar de todos os cálculos de senos para TODOS os ângulos notáveis, e você acabará trabalhando com um triângulo, tentando obter a resposta manualmente, e uma calculadora será útil para verificar novamente o que você obteve manualmente.

Além disso, você pode alimentar a calculadora com uma função sin, como sin(pi x), e em vez de calcular alguns pontos, esta calculadora fornecerá o gráfico correspondente

Quais são as etapas para usar uma calculadora de pecado?

• Passo 1: Identifique a expressão sin que você deseja calcular
• Passo 2: Digite a expressão na caixa correspondente. Você não precisa pré-simplificar, a calculadora fará isso por você
• Passo 3: A calculadora verificará se é uma expressão que pode ser avaliada, caso em que se reduzirá a seus termos mais simples
• Etapa 4: Se sin ainda estiver na expressão porque não foi possível simplificar mais, como sin(3/4), a calculadora fornecerá um valor numérico aproximado
• Etapa 5: Se uma função sin for fornecida, um gráfico será fornecido

Não podemos enfatizar o suficiente a importância de calcular corretamente as operações envolvendo seno, pois elas aparecerão literalmente em todos os lugares.

Fórmula seno e cos

Seno e cosseno são dois primos muito próximos, se não irmãs. Existe uma estreita relação entre eles, expressa na seguinte fórmula:

\[\displaystyle \sin\left(\frac{\pi}{2} - x \right) = \cos(x) \]

Além disso, outra fórmula que liga intimamente seno e cosseno é:

\[\displaystyle \sin^2(x) + \cos^2(x) = 1 \]

Por que o pecado é tão importante?

Os senos são importantes porque, junto com os cossenos, estão no centro e no núcleo da construção de um círculo. E então os círculos abrigam muitas outras construções, como triângulos e assim por diante.

Seno e cosseno acabam emaranhados em todas as construções geométricas, consequentemente.

Exemplo: calculadora de pecado

Calcule a seguinte expressão sin: \(\sin\left(\frac{\pi}{3}\right)\)

Solução: A seguinte expressão trigonométrica foi fornecida para ser calculada:

\[ \sin\left(\frac{\pi}{3}\right)\]

Ao inspecionar a expressão trigonométrica fornecida, podemos encontrar um ângulo notável, que é \(\sin\left(\frac{\pi{}}{3}\right)\).

▹ Para o ângulo \(\frac{\pi{}}{3}\) obtemos graficamente:

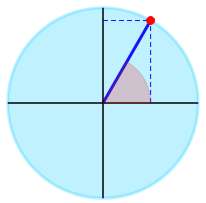
A expressão trigonométrica dada pode ser simplificada como:

Conclusão: Concluímos que \(\displaystyle \sin\left(\frac{\pi}{3}\right) = \frac{1}{2}\sqrt{3} \approx 0.866\).

Exemplo: mais cálculos de seno

Calcule o seguinte: \( \sin\left(\frac{5}{4}\right) \)

Solução: A seguinte expressão trigonométrica foi fornecida para ser calculada:

\[ \sin\left(\frac{5}{4}\right)\]

mas esta dada expressão trigonométrica não pode ser mais simplificada.

Conclusão: A função passada não pode ser simplificada e obtemos aproximadamente \(\displaystyle \sin\left(\frac{5}{4}\right) \approx 0.949\).

Exemplo: função sin

Calcule \( \sin(3x + 1) \).

Solução: Precisamos trabalhar com a seguinte função trigonométrica

\[f(x) = \sin\left(3x+1\right)\]

Com base no argumento da função trigonométrica passada, a frequência e o período são calculados da seguinte forma:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

e também

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

Com base na função trigonométrica fornecida, \(f(x) = \sin\left(3x+1\right)\), obtemos que:

» A amplitude neste caso é \(A = 1\).

» A mudança de fase é igual a \(\displaystyle\frac{-1}{3} = -0.3333\).

» O deslocamento vertical é igual a \( 0\).

Resumindo, o seguinte foi encontrado para a função trigonométrica dada

• Período = \(2.0944\)
• Frequência = \(0.4775\)
• Amplitude = \(1\)
• Mudança de Fase = \(-0.3333\)
• Deslocamento Vertical = \(\displaystyle 0\)

A seguir está o gráfico correspondente

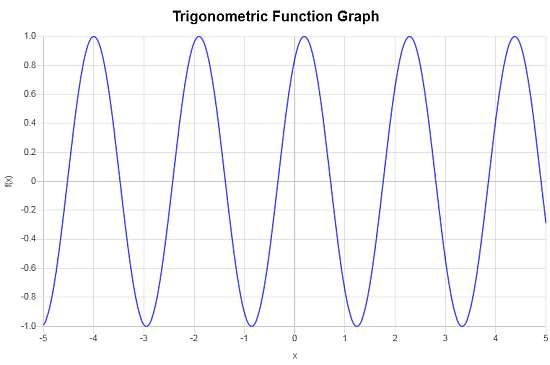
Mais calculadoras trigonométricas

A trigonometria combina todos esses conceitos, incluindo círculos e triângulos, e ambos pecado e porque estão no cerne disso.

Lidando com expressões trigonométricas é outra habilidade crucial que é muito importante para você adquirir.