Mais sobre esta calculadora trigonométrica

Isto calculadora trigonométrica permitirá que você avalie qualquer expressão trigonométrica fornecida. Certifique-se de fornecer qualquer expressão trigonométrica válida, pode ser algo direto como cos(pi/2) ou pode ser algo que não seja totalmente simplificado, como sin(1/3*pi+3/4*pi).

Você também pode fornecer uma função trigonométrica como sin(1/3*pi x +3/4*pi + x) e esta calculadora analisará e, se possível, fornecerá o período, frequência etc. gráfico .

Uma vez fornecida uma expressão trigonométrica válida, tudo o que você precisa fazer é clicar em "Calcular" e todas as etapas do cálculo serão mostradas para você.

expressões trigonométricas são bastante necessários, especialmente quando você está resolver triângulos . Normalmente é simples reduzir qualquer cálculo trigonométrico ao cálculo de alguns ângulos notáveis para o cosseno e deles .

Como fazer cálculos trigonométricos?

Fazer um cálculo trigonométrico pode ser uma tarefa muito geral e ampla, que pode ter estratégias específicas que funcionam melhor dependendo do cálculo trigonométrico específico que você precisa fazer e quais funções trigonométricas estão envolvidas, mas existem algumas estratégias gerais que podem servir bem.

Quais são as etapas para um cálculo trigonométrico

• Etapa 1: Identifique claramente a expressão trigonométrica que deseja calcular e simplifique os números e as frações o máximo que puder. Por exemplo, se você tiver cos(1+1/2), primeiro notará que 1+1/2 = 3/2, então na verdade você precisa de cos(3/2)
• Etapa 2: Uma vez que as frações possíveis e os números simples são agrupados e operados, se possível, determine se existem outras funções trigonométricas além do seno e do cosseno. Se houver, expresse tudo em termos de seno e cosseno
• Passo 3: Agora passe por todas as partes, que agora envolvem apenas seno e cosseno , e avaliar se existem ângulos notáveis envolvendo múltiplos ou frações de π
• Passo 4: Avalie diretamente essas expressões com notáveis ângulos que pode ser simplificado. Aqueles que não podem ser simplificados diretamente (se houver) são deixados como estão ou fornecem uma estimativa aproximada ( valor arredondado ) deles

É costume deixar como estão expressões que não conhecem, simplificações simples. Por exemplo, cos(1/4) não tem redução simples, então normalmente é deixado como está. Mas, por exemplo, cos(π/3) = 1/2, então essas reduções simples são obviamente realizadas

Calculadora de trigonometria com passos

A vantagem de esta calculadora é que ele mostrará todas as etapas relevantes do processo. O processo é simples: trata-se de simplificando expressões que envolvem apenas números, frações e expressões numéricas gerais diretamente avaliáveis.

Então, e somente então, você deve partir para o cálculo trigonométrico, para esclarecer as coisas o máximo possível antes de tentar qualquer cálculo trigonométrico.

Vantagens de usar um aplicativo de calculadora trigonométrica

Você pode pensar, bem, eu conheço muito bem minhas funções trigonométricas para ângulos notáveis básicos, então não preciso de um aplicativo de calculadora trigonométrica. Esse pode ser o caso, embora você possa hesitar um pouco, você é apresentado a algo como \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\).... você pode simplificá-lo? É um ângulo notável?

É realmente bom tentar resolver as coisas à mão e exercitar sua memória trigonométrica, mas um aplicativo de calculadora trigonométrica pode ajudá-lo, pelo menos, a verificar suas respostas.

Exemplo: cálculo trig

Calcule a expressão trigonométrica: \(\sin\left(\frac{5}{4}\pi\right)\)

Solução: A seguinte expressão trigonométrica foi fornecida para ser calculada:

\[ \sin\left(\frac{5\pi}{4}\right)\]

Ao inspecionar a expressão trigonométrica fornecida, podemos encontrar um ângulo notável, que é \(\sin\left(\frac{5\pi{}}{4}\right)\).

▹ Para o ângulo \(\frac{5\pi{}}{4}\) obtemos graficamente:

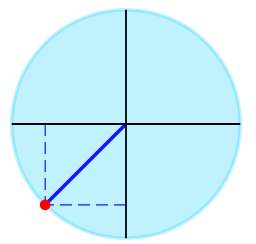
A expressão trigonométrica dada pode ser simplificada como:

Conclusão: Concluímos que \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0.7071\).

Exemplo: usando a calculadora trigonométrica

Reduzir: \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Solução: Agora precisamos trabalhar:

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

Este termo trigonométrico pode ser simplificado da seguinte forma:

Conclusão: Conclui-se que \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0.0125\).

Exemplo: simplificação de trigonometria

Calcule \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Solução: Ao inspecionar a expressão trigonométrica fornecida, podemos encontrar um ângulo notável, que é \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ Para o ângulo \(\frac{\pi{}}{4}\) obtemos graficamente:

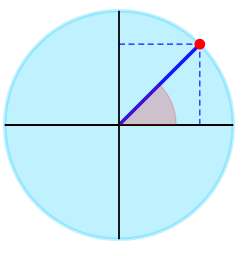
A expressão trigonométrica dada pode ser simplificada como:

Conclusão: Concluímos que \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0.8706\).

Mais calculadoras geométricas

Trabalhar com funções trigonométricas está intimamente relacionado com trabalhar com triângulos, portanto, ao trabalhar com um calculadora de triângulo você encontrará muitos cálculos trigonométricos.